数据挖掘与机器学习——离群点检测之孤立森林（isolate forest）

1.简单解释

利用二叉树和随机值，将数据分在左右。正常的自是子孙满堂，异常的显然孤家寡人。

2.概念基础

二叉搜索树、森林、随机森林、调和级数

二叉搜索树（二叉查找树/二叉排序树 ，Binary Search Tree，BST）

根节点的值大于其左子树中任意一个节点的值，小于其右节点中任意一节点的值。

调和级数举例：

 

 

 

3.理论定义

下面的英文翻译综合了已有的关于孤立森林的中文解释和对英文原本的基本翻译，而不是对于英文的直接汉化。在完成基本英文翻译过程中，对于句子进行了合理的断开和关键抽取。

Defifinition :Isolation Tree.

  Let T be a node of an isolation tree.

让T成为一个孤立森林的一个结点。

T is either an external-node with no child, or an internal-node with one test and exactly two daughter nodes (Tl,Tr).

当测试的时候，T没有孩子结点或者有两个孩子结点（左节点和右节点），当没有孩子结点时T为外部节点，当有两个孩子结点时T为内部结点。

这里外部节点指的是孤立点（离群点、异常点），内部结点则相反。

A test consists of an attribute q and a split value p such that the test q < p divides data points into Tl and Tr.

一个测试包含一个属性q和一个分割点p，利用分割点p可将属性q下的值分割至左右孩子。

Given a sample of data X = {x1, ..., xn} of n instances from a d-variate distribution, to build an isolation tree (iTree).

在建立一个孤立树（isolation tree,后简称iTree）的时候，给定一个数据集X。该数据集有n条数据，d个维度（即d个属性）。

We recursively divide X by randomly selecting an attribute q and a split value p, until either:

后将数据集X递归地进行划分，具体地，随机选择一个属性q和一个分割值p。既然是递归，则有终止条件，如下：

 （1）the tree reaches a height limit

       这个树达到了最大高度限度。

 （2）|X| = 1

       当前分割的X，只有一个结点。

（3）all data in X have the same values

       当前分割的X中的结点，有着相同的属性值。

An iTree is a proper binary tree, where each node in the tree has exactly zero or two daughter nodes.

一个符合要求的孤立树（即构建好的），是一个二叉树，并且它的每一个结点应该有0个孩子结点或者两个孩子结点。

这里需要与完全二叉树做区分。完全二叉树只有最后一层可以不满，并且有着从左到右的顺序，即最后一层不满时也应该在右边有所缺陷。而这里所说的树仅仅对于孩子节点数有要求。

 Assuming all instances are distinct, each instance is isolated to an external node when an iTree is fully grown, in which case the number of external nodes is n and the number of internal nodes is n-1; the total number of nodes of an iTrees is 2n-1; and thus the memory requirement is bounded and only grows linearly with n.

假设所有实例是不同的，当iTree完全成长时，每个实例被隔离成一个外部节点，此时外部节点数为n，内部节点数为n-1;iTrees节点总数为2n-1;因此内存需求是有界的并且只随着n线性增长。

We defifine path length and anomaly score as follows.

                         路径长度与异常分数

Defifinition : Path Length

路径长度

h(x) of a point x is measured by the number of edges x traverses an iTree from the root node until the traversal is terminated at an external node.

将点x作为外部节点时的路径长度定义为h(x)，该长度为从根节点到节点x经过的边数。

An anomaly score is required for any anomaly detection method. The difficulty in deriving such a score from h(x) is that while the maximum possible height of iTree grows in the order of n, the average height grows in the order of log n.

任何异常检测方法都需要一个异常分数。从h(x)中得出这样一个分数的困难在于，当iTree的最大可能高度以n阶增长时，平均高度以log(n)阶增长。

Normalization of h(x) by any of the above terms is either not bounded or cannot be directly compared.

上述任何一项对h(x)的归一化要么是没有边界的，要么是不能直接比较的。

Since iTrees have an equivalent structure to Binary Search Tree or BST (see Table 1), the estimation of average h(x) for external node terminations is the same as the unsuccessful search in BST.

由于孤立树与二叉搜索树（ Binary Search Tree，BST）具有相同的结构，所以外部节点终止的平均h(x)估计与BST中不成功搜索相同。

下表中，表示对应情况下的h(x)相等。

 

iTree	BST
Proper binary trees	Proper binary trees
External node termination 外部节点终止	Unsuccessful search 查找不成功
Not applicable 树不适用的时候	Successful search 查找成功

 

We borrow the analysis from BST to estimate the average path length of iTree.

我们利用BST来估计iTree的平均路径长度。

平均路径长度为：

 

注意此公式为2012年修正后。

where H(i) is the harmonic number and it can be estimated by ln(i) + 0.5772156649 (Euler’s constant). As c(n) is the average of h(x) given n, we use it to normalise h(x). The anomaly score s of an instance x is defifined as:

其中H(i)为调和级数，可以用ln(i) + 0.5772156649(欧拉常数)估计。

 

 

 

由于c(n)是给定n的h(x)的平均值，我们用它来规范化h(x)。实例x的异常分数s将被判定为:

 

where E(h(x)) is the average of h(x) from a collection of isolation trees.

其中E(h(x))是一系列孤立树h(x)的平均值。

• when E(h(x)) → c(n), s → 0.5;

• when E(h(x)) → 0, s → 1;

• and when E(h(x)) → n n 1, s → 0.

 

 

 

s is monotonic to h(x). Figure 2 illustrates the relationship between E(h(x)) and s, and the following conditions applied where 0 < s ≤ 1 for 0 < h(x) ≤ n -1. Using the anomaly score s, we are able to make the following assessment:

s对h(x)是单调的。图2给出了E(h(x))与s的关系，当0 < h(x)≤n -1时，0 < s≤1。利用异常分数s，我们可以做如下评估:

        • (a) if instances return s very close to 1, then they are definitely anomalies,

               s非常接近于1，则其为异常值。

         • (b) if instances have s much smaller than 0.5, then they are quite safe to be regarded as normal instances, and

              s远小于0.5，则其可视为正常值。

      • (c) if all the instances return s ≈ 0.5, then the entire sample does not really have any distinct anomaly.

             如果所有的s均约等于0.5，则样本实际上没有任何明显的异常。

 

4.实例与代码

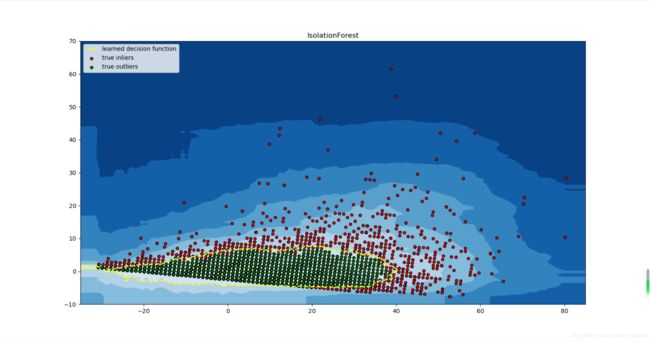
数据来自原开源项目，原数据一共有15000行数据，七个维度的数据。其中第一个数据属性数据为ip在数据利用时将其删掉，剩下六个维度的数据，进行为了方便可视化进行了降维处理，分析属性之间的相关性，将相关性大利用PCA降维，这里不过多赘述。

 

from sklearn.ensemble import IsolationForest
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

import pandas as pd
file="data3.xlsx"
data0 = pd.read_excel(file) #读取数据
data=np.array(data0)
#生成随机数的种子 “42”为随机数的种子，当种子相同时随机数相同
#计算机中的随机数生成并不是实际意义上的随机数生成 而是依靠等比（或者其他种类）数列形成，种子即初始值a1
rng = np.random.RandomState(42)
#题外话 下面的代码 依靠种子 生成0-1范围内的2行3列随机数
# randNum=rng.uniform(0,1,(2,3))


#选取数据的前8000行作为训练数据
X_train = data[:8000,:]
X_test = data
#max_samples 最大样本数，这里取得是数据集中总行数 ; random_state 随机种子
clf = IsolationForest(max_samples=15000,random_state=rng)
clf.fit(X_train)
y_pred_test = clf.predict(X_test)# 返回正常或者异常的标志，1是正常，-1是异常
scores_pred = clf.decision_function(data)
# 使用预测值取5%分位数来定义阈值（基于小概率事件5%）
outliers_fraction = 0.06
# 根据训练样本中异常样本比例，得到阈值，用于绘图
threshold = stats.scoreatpercentile(scores_pred, 100 * outliers_fraction)


# plot the line, the samples, and the nearest vectors to the plane
#meshgrid 生成网格点坐标矩阵
xx, yy = np.meshgrid(np.linspace(-35, 85, 100), np.linspace(-10, 70, 100))
#ravel() 扁平化函数，比如将二维排列的数变成一维
#decision_function 计算样本点到分割超平面的函数距离?
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])  # 正常分数，为正则为正常，为负可以认为是异常
#reshape() 将数据重新组织 比如将一维数据变二维数据
Z = Z.reshape(xx.shape)
#contourf（）用于画三维等高线图的，具体作用为填充轮廓
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)
# 绘制异常点区域与正常点区域的边界
a = plt.contour(xx, yy, Z, levels=[threshold], linewidths=2, colors='yellow')

#column_stack（）按列进行合并
resultData=np.column_stack(((data0['X'],data0['Y'],scores_pred,y_pred_test)))
df=pd.DataFrame(data=resultData,columns=['x', 'y', 'IsoFst_Score','label'])
b1 = plt.scatter(df['x'][df['label'] == -1], df['y'][df['label'] == -1], c='red',
                 s=20, edgecolor='k')
b2 = plt.scatter(df['x'][df['label'] == 1], df['y'][df['label'] == 1], c='green',
                 s=20, edgecolor='k')

plt.legend([a.collections[0], b1,b2],
               ['learned decision function', 'true inliers', 'true outliers'],
               loc="upper left")
plt.title("IsolationForest")
plt.axis('tight')
plt.xlim((-35, 85))
plt.ylim((-10, 70))
plt.show()

参考文献

[1]Liu, Fei Tony, Ting, Kai Ming and Zhou, Zhi-Hua. "Isolation forest." Data Mining, 2008. ICDM'08. Eighth IEEE International Conference on.
[2]Liu, Fei Tony, Ting, Kai Ming and Zhou, Zhi-Hua. "Isolation-based anomaly detection." ACM Transactions on Knowledge Discovery from Data (TKDD) 6.1 (2012): 3.

[3] isolation原理总结 博客园

[4] 机器学习-孤立森林 知乎

[5] SilenceSengku/IsolationForest2 github 代码参考

[6] 风控用户识别方法