图像分类数据集（Fashion-MNIST）

1、获取数据集

这也是我第一次接触到图像分类问题，在jupyter notebook上实现之后，还想把它写在博客上，为了纪念一下吧！ 首先对于原著的敬意，那肯定是要分享链接http://zh.gluon.ai/的啦！

1.1 获取数据集

首先导入需要的包和模块

In [1]: %matplotlib inline
        import gluonbook as gb
        from mxnet.gluon import data as gdata
        import sys
        import time

下⾯，我们通过Gluon 的data 包来下载这个数据集。第⼀次调⽤时会⾃动从⽹上获取数据。我们通过参数train 来指定获取训练数据集或测试数据集（testing data set）。测试数据集也叫测试集（testing set），只⽤来评价模型的表现，并不⽤来训练模型。

In [2]: mnist_train = gdata.vision.FashionMNIST(train=True)
        mnist_test = gdata.vision.FashionMNIST(train=False)

训练集中和测试集中的每个类别的图像数分别为6,000 和1,000。因为有10 个类别，所以训练集和测试集的样本数分别为60,000 和10,000。

In [3]: len(mnist_train), len(mnist_test)
Out[3]: (60000, 10000)

我们可以通过⽅括号[ ]来访问任意⼀个样本，下⾯获取第⼀个样本的图像和标签。

In [4]: feature, label = mnist_train[0]

变量feature 对应⾼和宽均为28 像素的图像。每个像素的数值为0 到255 之间8 位⽆符号整
数（uint8）。它使⽤3 维的NDArray 储存。其中的最后⼀维是通道数。因为数据集中是灰度图像，所以通道数为1。为了表述简洁，我们将⾼和宽分别为h 和w 像素的图像的形状记为h × w 或（h，w）。

In [5]: feature.shape, feature.dtype
Out[5]: ((28, 28, 1), numpy.uint8)

图像的标签使⽤NumPy 的标量表⽰。它的类型为32 位整数。

In [6]: label, type(label), label.dtype
Out[6]: (2, numpy.int32, dtype('int32'))

Fashion-MNIST 是⼀个10 类服饰分类数据集。Fashion-MNIST 中⼀共包括了10 个类别，分别为：t-shirt（T 恤）、trouser（裤⼦）、pullover（套衫）、dress（连⾐裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。以下函数可以将数值标签转成相应的⽂本标签。

In [7]: # 本函数已保存在gluonbook 包中⽅便以后使⽤。
        def get_fashion_mnist_labels(labels):
            text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                           'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
            return [text_labels[int(i)] for i in labels]

下⾯定义⼀个可以在⼀⾏⾥画出多张图像和对应标签的函数。

In [8]: # 本函数已保存在gluonbook 包中⽅便以后使⽤。
        def show_fashion_mnist(images, labels):
            gb.use_svg_display()
            # 这⾥的_ 表⽰我们忽略（不使⽤）的变量。
            _, figs = gb.plt.subplots(1, len(images), figsize=(12, 12))
            for f, img, lbl in zip(figs, images, labels):
                f.imshow(img.reshape((28, 28)).asnumpy())
                f.set_title(lbl)
                f.axes.get_xaxis().set_visible(False)
                f.axes.get_yaxis().set_visible(False)

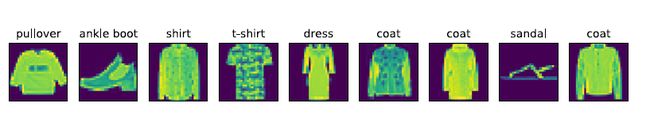
现在，我们看⼀下训练数据集中前9 个样本的图像内容和⽂本标签。

In [9]: X, y = mnist_train[0:9]
        show_fashion_mnist(X, get_fashion_mnist_labels(y))

1.2 读取小批量

我们将在训练数据集上训练模型，并将训练好的模型在测试数据集上评价模型的表现。虽然我
们可以像“线性回归的从零开始实现”⼀节中那样通过yield 来定义读取小批量数据样本的
函数，但为了代码简洁，这⾥我们直接创建DataLoader 实例。该实例每次读取⼀个样本数为
batch_size 的小批量数据。这⾥的批量⼤小batch_size 是⼀个超参数。
在实践中，数据读取经常是训练的性能瓶颈，特别当模型较简单或者计算硬件性能较⾼时。Gluon的DataLoader 中⼀个很⽅便的功能是允许使⽤多进程来加速数据读取（暂不⽀持Windows操作系统）。这⾥我们通过参数num_workers 来设置4 个进程读取数据。
此外，我们通过ToTensor 类将图像数据从uint8 格式变换成32 位浮点数格式，并除以255 使
得所有像素的数值均在0 到1 之间。ToTensor 类还将图像通道从最后⼀维移到最前⼀维来⽅便
之后介绍的卷积神经⽹络计算。通过数据集的transform_first 函数，我们将ToTensor 的
变换应⽤在每个数据样本（图像和标签）的第⼀个元素，即图像之上。

In [10]: batch_size = 256
         transformer = gdata.vision.transforms.ToTensor()
         if sys.platform.startswith('win'):
             num_workers = 0        # 0 表⽰不⽤额外的进程来加速读取数据。
         else:
             num_workers = 4
         train_iter = gdata.DataLoader(mnist_train.transform_first(transformer),
                                       batch_size, shuffle=True,
                                       num_workers=num_workers)
         test_iter = gdata.DataLoader(mnist_test.transform_first(transformer),
                                       batch_size, shuffle=False,
                                       num_workers=num_workers)

我们将获取并读取Fashion-MNIST 数据集的逻辑封装在gluonbook.load_data_fashion_mnist 函数中供后⾯章节调⽤。该函数将返回train_iter 和test_iter 两个变量。随着本书内容的不断深⼊，我们会进⼀步改进该函数。它的完整实现将在“深度卷积神经⽹络（AlexNet）”⼀节中描述。
最后我们查看读取⼀遍训练数据需要的时间。

In [11]: start = time.time()
         for X, y in train_iter:
             continue
         '%.2f sec' % (time.time() - start)
Out[11]: '1.09 sec'

2、Softmax 回归的从零开始实现

这⼀节我们来动⼿实现Softmax 回归。⾸先导⼊本节实现所需的包或模块。

In [1]: %matplotlib inline
        import gluonbook as gb
        from mxnet import autograd, nd

2.1 获取和读取数据

我们将使⽤Fashion-MNIST 数据集，并设置批量⼤小为256。

In [2]: batch_size = 256
        train_iter, test_iter = gb.load_data_fashion_mnist(batch_size)

2.2 初始化模型参数

跟线性回归中的例⼦⼀样，我们将使⽤向量表⽰每个样本。已知每个样本输⼊是⾼和宽均为28
像素的图像。模型的输⼊向量的⻓度是28 × 28 = 784：该向量的每个元素对应图像中每个像素。
由于图像有10 个类别，单层神经⽹络输出层的输出个数为10。所以Softmax 回归的权重和偏差
参数分别为784 × 10 和1 × 10 的矩阵。

In [3]: num_inputs = 784
        num_outputs = 10
        W = nd.random.normal(scale=0.01, shape=(num_inputs, num_outputs))
        b = nd.zeros(num_outputs)

同之前⼀样，我们要对模型参数附上梯度。

In [4]: W.attach_grad()
        b.attach_grad()

2.3 实现Softmax 运算

在介绍如何定义Softmax 回归之前，我们先描述⼀下对如何对多维NDArray 按维度操作。在下⾯
例⼦中，给定⼀个NDArray 矩阵X。我们可以只对其中同⼀列（axis=0）或同⼀⾏（axis=1）
的元素求和，并在结果中保留⾏和列这两个维度（keepdims=True）。

In [5]: X = nd.array([[1, 2, 3], [4, 5, 6]])
        X.sum(axis=0, keepdims=True), X.sum(axis=1, keepdims=True)

Out[5]: (
         [[5. 7. 9.]]
         ,
         [[ 6.]
         [15.]]
         )

下⾯我们就可以定义前⾯小节⾥介绍的softmax 运算了。在下⾯的函数中，矩阵X 的⾏数是样
本数，列数是输出个数。为了表达样本预测各个输出的概率，softmax 运算会先通过exp 函数对
每个元素做指数运算，再对exp 矩阵同⾏元素求和，最后令矩阵每⾏各元素与该⾏元素之和相
除。这样⼀来，最终得到的矩阵每⾏元素和为1 且⾮负。因此，该矩阵每⾏都是合法的概率分布。
Softmax 运算的输出矩阵中的任意⼀⾏元素代表了⼀个样本在各个输出类别上的预测概率。

In [6]: def softmax(X):
            X_exp = X.exp()
            partition = X_exp.sum(axis=1, keepdims=True)
            return X_exp / partition # 这⾥应⽤了⼴播机制。

可以看到，对于随机输⼊，我们将每个元素变成了⾮负数，且每⼀⾏和为1。

In [7]: X = nd.random.normal(shape=(2, 5))
        X_prob = softmax(X)
        X_prob, X_prob.sum(axis=1)

Out[7]: (
         [[0.21324193 0.33961776 0.1239742 0.27106097 0.05210521]
          [0.11462264 0.3461234 0.19401033 0.29583326 0.04941036]]
         ,
         [1.0000001 1. ]
         )

2.4 定义模型

有了softmax 运算，我们可以定义上节描述的softmax 回归模型了。这⾥通过reshape 函数将
每张原始图像改成⻓度为num_inputs 的向量。

In [8]: def net(X):
            return softmax(nd.dot(X.reshape((-1, num_inputs)), W) + b)

2.5 定义损失函数

上⼀节中，我们介绍了softmax 回归使⽤的交叉熵损失函数。为了得到标签的预测概率，我们可
以使⽤pick 函数。在下⾯例⼦中，变量y_hat 是2 个样本在3 个类别的预测概率，变量y
是这2 个样本的标签类别。通过使⽤pick 函数，我们得到了2 个样本的标签的预测概率。与
“Softmax 回归”⼀节数学表述中标签类别离散值从1 开始逐⼀递增不同，在代码中，标签类别的
离散值是从0 开始逐⼀递增的。

In [9]: y_hat = nd.array([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
        y = nd.array([0, 2])
        nd.pick(y_hat, y)

Out[9]:
        [0.1 0.5]
        

以下实现了“Softmax 回归”⼀节中介绍的交叉熵损失函数。

In [10]: def cross_entropy(y_hat, y):
             return - nd.pick(y_hat, y).log()

2.6 计算分类准确率

给定⼀个类别的预测概率分布y_hat，我们把预测概率最⼤的类别作为输出类别。如果它与真
实类别y ⼀致，说明这次预测是正确的。分类准确率即正确预测数量与总预测数量之⽐。
下⾯定义准确率accuracy 函数。其中y_hat.argmax(axis=1) 返回矩阵y_hat 每⾏中最
⼤元素的索引，且返回结果与变量y 形状相同。我们在“数据操作”⼀节介绍过，相等条件判断
式(y_hat.argmax(axis=1) == y) 是⼀个值为0（相等为假）或1（相等为真）的NDArray。
由于标签类型为整数，我们先将变量y 变换为浮点数再进⾏相等条件判断。

In [11]: # 本函数已保存在gluonbook 包中⽅便以后使⽤。
         def accuracy(y_hat, y):
             return (y_hat.argmax(axis=1) == y.astype('float32')).mean().asscalar()

让我们继续使⽤在演⽰pick 函数时定义的变量y_hat 和y，并将它们分别作为预测概率分
布和标签。可以看到，第⼀个样本预测类别为2（该⾏最⼤元素0.6 在本⾏的索引为2），与真实
标签0 不⼀致；第⼆个样本预测类别为2（该⾏最⼤元素0.5 在本⾏的索引为2），与真实标签2
⼀致。因此，这两个样本上的分类准确率为0.5。

In [12]: accuracy(y_hat, y)
Out[12]: 0.5

类似地，我们可以评价模型net 在数据集data_iter 上的准确率。

In [13]: # 本函数已保存在gluonbook 包中⽅便以后使⽤。该函数将被逐步改进：它的完整实现将在“图像增⼴”⼀节中描述。
         def evaluate_accuracy(data_iter, net):
             acc = 0
             for X, y in data_iter:
                 acc += accuracy(net(X), y)
             return acc / len(data_iter)

因为我们随机初始化了模型net，所以这个随机模型的准确率应该接近于类别个数10 的倒数
0.1。

In [14]: evaluate_accuracy(test_iter, net)
Out[14]: 0.0947265625

2.7 训练模型

训练softmax 回归的实现跟前⾯介绍的线性回归中的实现⾮常相似。我们同样使⽤小批量随机梯
度下降来优化模型的损失函数。在训练模型时，迭代周期数num_epochs 和学习率lr 都是可
以调的超参数。改变它们的值可能会得到分类更准确的模型。

In [15]: num_epochs, lr = 5, 0.1
         # 本函数已保存在gluonbook 包中⽅便以后使⽤。
         def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
                       params=None, lr=None, trainer=None):
             for epoch in range(num_epochs):
                 train_l_sum = 0
                 train_acc_sum = 0
                 for X, y in train_iter:
                     with autograd.record():
                          y_hat = net(X)
                          l = loss(y_hat, y)
                     l.backward()
                     if trainer is None:
                         gb.sgd(params, lr, batch_size)
                     else:
                         trainer.step(batch_size) # 下⼀节将⽤到。
                     train_l_sum += l.mean().asscalar()
                     train_acc_sum += accuracy(y_hat, y)
             test_acc = evaluate_accuracy(test_iter, net)
             print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
                   % (epoch + 1, train_l_sum / len(train_iter),
                      train_acc_sum / len(train_iter), test_acc))
         train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs,
                   batch_size, [W, b], lr)
                   
Out [15]: epoch 1, loss 0.7867, train acc 0.749, test acc 0.798
          epoch 2, loss 0.5744, train acc 0.810, test acc 0.825
          epoch 3, loss 0.5295, train acc 0.822, test acc 0.831
          epoch 4, loss 0.5049, train acc 0.831, test acc 0.830
          epoch 5, loss 0.4903, train acc 0.834, test acc 0.838

2.8 预测

训练完成后，现在我们可以演⽰如何对图像进⾏分类。给定⼀系列图像（第三⾏图像输出），我
们⽐较⼀下它们的真实标签（第⼀⾏⽂本输出）和模型预测结果（第⼆⾏⽂本输出）。

In [16]: for X, y in test_iter:
             break
         true_labels = gb.get_fashion_mnist_labels(y.asnumpy())
         pred_labels = gb.get_fashion_mnist_labels(net(X).argmax(axis=1).asnumpy())
         titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]
         gb.show_fashion_mnist(X[0:9], titles[0:9])