算法——快速排序、希尔排序、堆排序

上一篇文章 简单算法——直接插入、冒泡、直接选择介绍了简单排序法，本文在上一篇的基础上，介绍各简单排序法对应的高级算法。
首先依然是做一个公共的元素置换函数

/**
     * 交换数组元素
     * 交换思想很简单 数字x y  =>  x=x+y;y=x-y;x=x-y;
     * 这种方法不使用临时变量，能有效降低算法空间复杂度，但也有缺点，比如可能存在越界风险
     * @param arr
     * @param a
     * @param b
     */
    public void swap(int []arr,int a,int b){
        arr[a] = arr[a]+arr[b];
        arr[b] = arr[a]-arr[b];
        arr[a] = arr[a]-arr[b];
    }

快速排序

快速排序（Quicksort）是对冒泡排序的一种改进。
基本思想：第一趟将数据分割成两部分，其中一部分的所有数据都比另外一部分都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，直到整个数据变成有序序列。
基本操作：
1、设置两个变量i、j，排序开始的时候：i=0，j=n-1；
2、以第一个数组元素作为关键数据，赋值给key，即key=A[0]；
3、从j开始向前搜索，即由后开始向前搜索(j–)，找到第一个小于key的值A[j]，将A[j]和A[i]互换；
4、从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]互换；
5、重复第3、4步，直到i=j；
如：
原始数组[5, 3, 6, 4, 8, 7, 9]
第一轮快速排序：
根据基本操作1、2 ：设置变量 key=5,i=0,j=7
根据基本操作3,操作 j 得到：4 3 6 5 8 7 9（i=0,j=3,a[j]=5,a[i]=4）
根据基本操作4，操作 i 得到：4 3 5 6 8 7 9（i=2,j=3,a[i]=5,a[j]=6）
根据基本操作3,操作 j，当j等于2时，发现i==j，此时第一趟快速排序结束，此时得到： 4 3 5 6 8 7 9发现所有比key(6)值大的都在右边，比key小的都在左边！

然后，对key两边的数据，再分别进行上述的过程，直到不能再分组为止。
代码实现：

    int arr[] = {5, 3, 6, 4, 8, 7, 9};
    quickSort(arr,0,arr.length-1);
    public void quickSort(int[] arr, int low, int high){
         if(low >= high) {
            return;
        }
        System.out.print(" k = " + ++k);
        //基本操作1、2
        int i = low;
        int j = high;
        int key = arr[low];
        while (i//基本操作3
            while (i < j && arr[j] >= key){
                j--;
            }
            if(i < j) {
                swap(arr, i++, j);
            }

            //基本操作4
            while (i < j && arr[i] < key){
                i++;
            }
            if(i < j) {
                swap(arr, i, j--);
            }
        }
        //对key两边的数据，再分别进行上述的过程
        quickSort(arr,low,i-1);
        quickSort(arr,i+1,high);
    }

快速排序有很多变种，如三平均分区法、随机化快排等，这里不多做介绍！

希尔排序

希尔排序(Shell’s Sort)是直接插入排序算法的一种更高效的改进版本。
基本思想：先取一个正整数 d1 < n 作为第一个增量，把数组中所有相隔d1的数据对归为一组，组内进行直接插入排序；然后取 d2 < d1 ,重复上述操作，直至di = 1,即所有记录放在同一组中进行直接插入排序为止。(一般d1=n/2，以后每次减半，若结果为偶数，则加1，确保后续增量为奇数)。

原始数组 5,3,6,4,8,7,9
第一步：d1取3 ，将相隔为3的数据分为一组，组内进行直接插入排序
[5,4,9] [3,8] [6,7] —> 4 3 6 5 8 7 9
第二步：d2=1，将相隔为1的数据分为一组，组内进行直接插入排序
[5,3,6,4,8,7,9] —> 3 4 5 6 7 8 9

代码实现

   int arr[] = {5, 3, 6, 4, 8, 7, 9};
   public void sort(int[] arr) {
        //增量gap，并逐步缩小增量
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            //从第gap个元素，逐个对其所在组进行直接插入排序操作
            directSort(arr, gap);
        }
    }

    //这里就是简单插入排序了，详细可查看上一篇文章
    public void directSort(int[] arr, int gap) {
        for (int i = 0; i < arr.length; i++) {
            int j = i;
            while (j + gap <=arr.length-1 && arr[j] > arr[j + gap]){
                swap(arr, j, j + gap);
                j += gap;
            }
        }
    }

堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。
小根堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2];大根堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] 。本文以大根堆（升序）为例！
基本操作：
①建堆：建堆是不断调整堆的过程，从len/2处开始调整，一直到第一个节点；
②调整堆：调整堆就是比较节点i和其子节点left(i),right(i)，选出三者最大(或者最小)者，如果最大值不是节点i而是它的一个子节点，就进行交换，然后重复这个过程。
③堆排序：堆排序是利用上面的两个过程来进行的。先取出根节点，然后前面len-1个节点继续进行堆调整的过程，接着再将根节点取出直到所有节点都取出。
这种排序需要对“树”有一定的了解：
原始数组 [5,3,6,4,8,7,9] 可以转换成下图二叉树结构

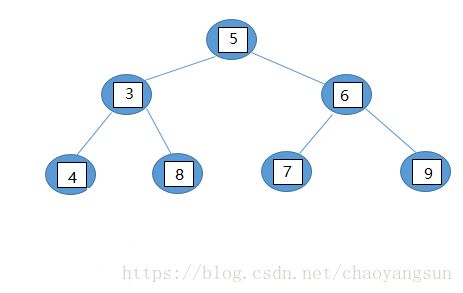
程序实现

     int arr[] = {5, 3, 6, 4, 8, 7, 9};
     //构建大顶堆
     buildMaxHeapify(arr);
     //堆排序
     heapSort(arr);

    /**
     *排序，最大值放在末尾，arr虽然是最大堆，在排序后就成了递增的
     *
     *@paramarr
     */
    private static void heapSort(int[] arr){
        //末尾与头交换，交换后调整最大堆
        for(int i=arr.length-1;i>0;i--){
            swap(arr, 0, i);
            maxHeapify(arr,i,0);
        }
    }

    /**
     * 建堆
     * @param arr
     */
    private static void buildMaxHeapify(int[] arr){
        //从最后一个的父节点开始
        int startIndex=getParentIndex(arr.length-1);
        //从下至上，从右至左调整
        for(int i=startIndex;i>=0;i--){
            maxHeapify(arr,arr.length,i);
        }
    }

    /**
     *调整堆
     */
    private static void maxHeapify(int[] arr,int size,int index){
        //获取左子节点下标 等价于index*2+1
        int left = (index<<1) + 1;
        //获取右子节点下标 等价于index*2+2
        int right = (index<<1) + 2;

        //当前点与左右子节点比较
        int largest=index;
        if(leftif(right//得到最大值后可能需要交换，如果交换了，其子节点可能就不是最大堆了，需要重新调整
        if(largest!=index){
            swap(arr, index, largest);
            maxHeapify(arr,size,largest);
        }
    }

    /**
     *父节点位置
     *@return 等价于(current-1)/2 如：(4-1)/2等于1 等价于二进制0011向右移动一位0001
     */
    private static int getParentIndex(int current){
        return(current-1)>>1;//>>表示向右移动一位
    }

参考
快速排序算法
白话经典算法系列
图解排序算法系列
堆排序