算法学习—001—js实现插入排序—insertSort

插入排序：对于少量元素比较有效。

工作方式：像排序一手扑克牌，开始时，我们的左手为空并且桌子上的牌面向下。然后，我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较，如图2-1所示。拿在左手上的牌总是排序好的，原来这些牌是桌子上牌堆中顶部的牌。

对于插入排序，我们将其伪代码过程命名为INSERTION-SORT，其中的参数是一个数组A［1..n］，包含长度为n的要排序的一个序列。（在代码中，A中元素的数目n用A.length来表示。）该算法原址排序输入的数：算法在数组A中重排这些数，在任何时候，最多只有其中的常数个数字存储在数组外面。在过程INSERTION-SORT结束时，输入数组A包含排序好的输出序列。
INSERTION-SORT(A)
1　for j = 2 to A.length
2　　key = A［j］
3　　// Insert A［j］ into the sorted sequence A［1..j - 1］.
4　　i = j - 1
5　　while i > 0 and A［i］ > key
6　　　　A［i+1］ = A［i］
7　　　　i = i - 1
8　　A［i + 1］ = key

循环不变式与插入排序的正确性

 

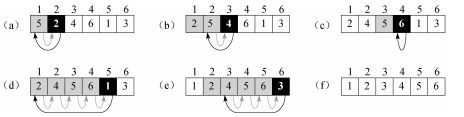
图2-2表明对A=〈5,2,4,6,1,3〉该算法如何工作。下标j指出正被插入到手中的“当前牌”。在for循环（循环变量为j）的每次迭代的开始，包含元素A［1..j-1］的子数组构成了当前排序好的左手中的牌，剩余的子数组A［j+1..n］对应于仍在桌子上的牌堆。事实上，元素A［1..j-1］就是原来在位置1到j-1的元素，但现在已按序排列。我们把A［1..j-1］的这些性质形式地表示为一个循环不变式：

在第1～8行的for循环的每次迭代开始时，子数组A［1..j-1］由原来在A［1..j-1］中的元素组成，但已按序排列。

图2-2　在数组A=〈5,2,4,6,1,3〉上INSERTION-SORT的操作。数组下标出现在长方形的上方，数组位置中存储的值出现在长方形中。（a)～（e)第1～8行for循环的迭代。每次迭代中，黑色的长方形保存取自A［j］的关键字，在第5行的测试中将它与其左边的加阴影的长方形中的值进行比较。加阴影的箭头指出数组值在第6行向右移动一个位置，黑色的箭头指出在第8行关键字被移到的地方。（f)最终排序好的数组。

用js实现

insertSort