数据预处理概念

数据预处理的常用流程：

　　　　1）去除唯一属性

　　　　2）处理缺失值

　　　　3）属性编码

　　　　4）数据标准化、正则化

　　　　5）特征选择

　　　　6）主成分分析

1、去除唯一属性

　　如id属性，是唯一属性，直接去除就好

2、处理缺失值

(1)直接使用含有缺失值的特征

　　如决策树算法就可以直接使用含有缺失值的特征

(2)删除含有缺失值的特征

(3)缺失值补全(最广泛运用)

用最可能的值来插补缺失值

1)均值插补

　　若样本属性的距离是可度量的，则该属性的缺失值就以该属性有效值的平均值来插补缺失的值。如果样本的属性的距离是不可度量的，则该属性的缺失值就以该属性有效值的众数来插补缺失的值。

2)用同类均值插补

　　首先将样本进行分类，然后以该类样本中的均值来插补缺失值。

3)建模预测

　　将缺失的属性作为预测目标来预测。这种方法效果较好，但是该方法有个根本的缺陷：如果其他属性和缺失属性无关，则预测的结果毫无意义。但是如果预测结果相当准确，则说明这个缺失属性是没必要考虑纳入数据集中的。一般的情况介于两者之间。

4)高维映射

　　将属性高映射到高维空间。这种做法是最精确的做法，它完全保留了所有的信息，也未增加任何额外的信息。这样做的好处是完整保留了原始数据的全部信息、不用考虑缺失值。但它的缺点也很明显，就是计算量大大提升。而且只有在样本量非常大的时候效果才好，否则会因为过于稀疏，效果很差。

5)多重插补

　　多重插补认为待插补的值是随机的，它的值来自于已观测到的值。具体实践上通常是估计出待插补的值，然后再加上不同的噪声，形成多组可选插补值。根据某种选择依据，选取最合适的插补值。

6)极大似然估计

7)压缩感知及矩阵补全

　　压缩感知通过利用信号本身所具有的稀疏性，从部分观测样本中回复原信号。压缩感知分为感知测量和重构恢复两个阶段。

　　　　感知测量：此阶段对原始信号进行处理以获得稀疏样本表示。常用的手段是傅里叶变换、小波变换、字典学习、稀疏编码等

　　　　重构恢复：此阶段基于稀疏性从少量观测中恢复原信号。这是压缩感知的核心

　　矩阵补全

3、特征编码

(1)特征二元化：将数值型的属性转换成布尔型的属性

(2)独热编码：构建一个映射，将这些非数值属性映射到整数。其采用N位状态寄存器来对N个可能的取值进行编码，每个状态都由独立的寄存器位表示，并且在任意时刻只有其中的一位有效。

4、数据标准化、正则化

(1)数据标准化：将样本的属性缩放到某个指定范围

　　进行数据标准化的原因：一是因为某些算法要求样本数据具有零均值和单位方差。二是样本不同属性具有不同量级时，消除数量级的影响。

　　min-max标准化：标准化之后，样本x的所有属性值都在[0,1]之间

　　z-score标准化：标准化之后，样本集的所有属性的均值都是0，标准差均为1

(2)数据正则化：将样本的某个范数（如L1范数）缩放到单位1。正则化的过程是针对单个样本的，对于每个样本将样本缩放到单位范数。通常如果使用二次型（如点积）或者其他核方法计算两个样本之间的相似性，该方法会很有用。

5、特征选择

(1)过滤式选择：先对数据集进行特征选择，然后再训练学习器。特征选择过程与后续学习器无关。常用方法有Relief（二分类）、Relief-F（多分类）

(2)包裹式选择：直接把最终将要使用的学习器的性能作为特征子集的评价准则。常用方法LVW

(3)嵌入式选择和L1正则化

　　嵌入式特征选择是在学习器训练过程中自动进行了特征选择

6、稀疏表示和字典学习

---

数据预处理实战总结：

---

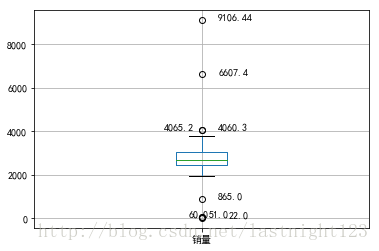
1、绘制箱型图判断数据是否有异常值

　　运用Python的Pandas库中，读入数据，然后使用describe()函数查看数据的基本情况
　　

import pandas as pd
import numpy as np
#文件地址
catering_sale = 'E:/PyCharm/MyPyCharm/Python_data_analysis/chapter3/demo/data/catering_sale.xls'
#pd.read_excel()用于读取文件
data = pd.read_excel(catering_sale, index_col=r'日期')

#数据描述，其中count可以得到非空值数
#运用data.describe与len对比得到空值个数
data.describe()
len(data)

# df.index 是获取行名称，对应后面的[0]取行号/通过以下方式
np.where(data.isnull())#可以获取NAN的行号，如下为14行
    (array([14], dtype=int64), array([0], dtype=int64))
data.index[np.where(data.isnull())[0]]#可以获取NAN的索引，如下为'2015-02-14'
    DatetimeIndex(['2015-02-14'], dtype='datetime64[ns]', name='日期', freq=None)

#绘制箱型图
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号

plt.figure() #建立图像
p = data.boxplot(return_type='dict') #画箱线图，直接使用DataFrame的方法
x = p['fliers'][0].get_xdata() # 'flies'即为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort() #从小到大排序，该方法直接改变原对象

#用annotate添加注释
#其中有些相近的点，注解会出现重叠，难以看清，需要一些技巧来控制。
#以下参数都是经过调试的，需要具体问题具体调试。
for i in range(len(x)): 
  if i>0:
    plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]),y[i]))
  else:
    plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.08,y[i]))

plt.show() #展示箱线图

　　通过绘制箱型图可以筛选查看出异常数据，箱型图识别异常值的结果比较客观，在识别异常值方面有一定的优越性，超过上下界的数据为可疑的异常值，然后通过编写过滤程序，进行后续处理。
　　

---

2、数据清洗

　　运用拉格朗日插值法《python数据分析与挖掘实战P63》
　　from scipy.interpolate import lagrange #导入拉格朗日插值函数

# -*- coding:utf-8 -*-
# __author__ = 'Administrator'

#拉格朗日插值代码
import pandas as pd #导入数据分析库Pandas
from scipy.interpolate import lagrange #导入拉格朗日插值函数

inputfile = '../data/catering_sale.xls' #销量数据路径
outputfile = '../text/sales.xls' #输出数据路径

data = pd.read_excel(inputfile) #读入数据
# print(data)
data[u'销量'][(data[u'销量'] < 400) | (data[u'销量'] > 5000)] = None #过滤异常值，将其变为空值

#自定义列向量插值函数
#s为列向量，n为被插值的位置，k为取前后的数据个数，默认为5
def ployinterp_column(s, n, k=5):
  y = s[list(range(n-k, n)) + list(range(n+1, n+1+k))] #取数
  y = y[y.notnull()] #剔除空值
  return lagrange(y.index, list(y))(n) #插值并返回插值结果

#逐个元素判断是否需要插值
for i in data.columns:
  for j in range(len(data)):
    if (data[i].isnull())[j]: #如果为空即插值。
      data[i][j] = ployinterp_column(data[i], j)

data.to_excel(outputfile) #输出结果，写入文件

　　在进行插值之前会对数据进行异常值检查，数据大于5000以及数据小于400的会被过滤检测出来（通过第一步的箱型图得来），然后再使用拉格朗日插值法填补数据。
　　很多情况下，要先分析异常值出现的可能原因，在判断异常值是否应该被舍弃，如果是正确的数据，可以直接在具有异常值的数据集上进行数据挖掘。

---

3、数据标准化

　　主要在sklearn.preprcessing包下。
　　
　　我们都知道大多数的梯度方法（几乎所有的机器学习算法都基于此）对于数据的缩放很敏感。
　　
　　scikit-learn中的preprocessing提供了数据预处理的工具
　　《Python大战机器学习 P316》数据标准化：二元化、独热码one-hot、标准化、正则化
　　

1）二元化
　　scikit-learn提供的Binarizer能够实现数据二元化

from sklearn.preprocessing import Binarizer

#class sklearn.preprocessing.Binarizer(threshold=0.0, copy=True)
#threshold用于指定阈值，大于此阈值的数标记为1，小于此阈值的数为0
X = [[1, 2, 3, 4, 5],
     [5, 4, 3, 2, 1],
     [3, 3, 3, 3, 3],
     [1, 1, 1, 1, 1]]
print("before transfom:",X)
binarizer = Binarizer(threshold=2.5)
print("after transform:",binarizer.transform(X))

#### 结果 ####
before transfom: 
[[1, 2, 3, 4, 5], 
[5, 4, 3, 2, 1], 
[3, 3, 3, 3, 3], 
[1, 1, 1, 1, 1]]
after transform: 
[[0 0 1 1 1]
 [1 1 1 0 0]
 [1 1 1 1 1]
 [0 0 0 0 0]]

2）独热码
　　

快速了解原理：

http://blog.clzg.cn/blog-1579109-884831.html

　　scikit-learn提供的OneHotEncoder能够实现数据独热码

from sklearn.preprocessing import OneHotEncoder

X = [[1, 2, 3, 4, 5],
     [5, 4, 3, 2, 1],
     [3, 3, 3, 3, 3],
     [1, 1, 1, 1, 1]]
print("before transfom:",X)
encoder = OneHotEncoder(sparse=False)
encoder.fit(X)
print("active_features_:",encoder.active_features_)
print("feature_indices_:",encoder.feature_indices_)
print("n_values_:",encoder.n_values_)
print("after transform:",encoder.transform([[1,2,3,4,5]]))

#### 结果 ####
before transfom: 
[[1, 2, 3, 4, 5], 
[5, 4, 3, 2, 1], 
[3, 3, 3, 3, 3], 
[1, 1, 1, 1, 1]]
active_features_: [ 1  3  5  7  8  9 10 12 14 16 17 18 19 21 23 25]
feature_indices_: [ 0  6 11 15 20 26]
n_values_: [6 5 4 5 6]
after transform: 
[[ 1.  0.  0.  0.  1.  0.  0.  0.  1.  0.  0.  0.  1.  0.  0.  1.]]