白话机器学习: 模型性能评价
文章目录
- 假设空间
- 性能评价
- 评估方法
- 留出法
- 交叉验证法
- 自助法
- 性能度量
- 错误率与精度
- 查准率 & 查全率
- P-R图
- ROC & AUC
- 代价敏感错误与代价曲线
假设空间
在周志华老师的《机器学习》一书中提到,模型的训练就是利用训练数据在数据属性构成的“假设空间”中进行搜索,在搜索过程中会删除假设空间的某些假设,最终留下一些假设形成“版本空间”,最终再通过这个模型进行推理。
至于什么是假设空间,假设的删除是怎么生成的,搬运一篇博客,讲的非常清楚:
性能评价
机器学习算法是想通过已有的数据来构建模型进行预测,预测的是好是坏,我们需要对算法进行评估。
实际上我理解这种评估就和我们日常参加考试是一个道理:日常我们做的习题是训练我们的考试能力,我们称之为“训练集”;那么考试题目就是测试我们被训练的怎么样,称之为“测试集”。毕业之后,是否能根据训练和测试的数据进行举一反三,解决实际问题,就看我们自己这个“模型”的泛化能力了。
那么选择哪些题做平时的习题,哪些做考题呢?这个是提高我们考试能力和解决问题能力的一个关键。全部挑容易的做习题,考试考不过。全部挑难的,又会失去一般性。
学习算法和这个类似,如何挑选样本作为训练集和测试集,一般有几种方法。和选习题不一样的是,习题一般来说还是选择一些会考的原题,让考生们心里有点信心;而算法训练的话,一般是会保证训练集和测试集无交集。
那么我们怎么去划分样本对学习算法进行评估呢,一般来说有以下3中评估方法:
- 留出法
- 交叉验证法
- 自助法
介绍完评估方法后,我们看一下用哪些指标来量化一个评估方法的好坏。
评估方法
留出法
留出法就是将整个数据样本集按照某种原则直接分成s和t两个集合。这个原则有以下几点考虑:
- 分层采样。比如数据样本是一个二分类问题,那么尽量保证测试集中的正例/反例的比例与数据样本的整体比例相同。测试集相同了训练集自然也相同。比如总共1000个样本,700个正例,300个反例。假设训练集选择700个样例,如果全部把正例放进去,泛化能力肯定不行,保证490个正例在训练集,210个在测试集中会效果比较好。
- 一次划分往往无法准确的评估,需要按同一个原则划分n次,然后进行n次评估后求平均值。某个样本(xi,yi)在n次划分中会反复出现在训练集和测试集中。
- 常见的划分为2/3 - 4/5为训练集,其余的为测试集。训练集太大,导致测试集小无法准确评估,若训练集太小则直接无法拟合全局状态。
交叉验证法
交叉验证法我理解是留出法的一种具体操作方式,就是将整个数据样本划分成k个集合,用其中k-1个集合的并集作为训练集,另外的一个作为测试集。从k = 1一直到k = k,每个集合都会成为一次测试集。总共做k次评估,求平均值。
此时,k的取值是比较关键的参数,算法中的调参指的就是调整这种参数。参数不同,算法的性能会出现比较大的变化。
自助法
假设一个m个样本的数据样本集d,从整体样本中随机挑选一个样本放入到训练集d-中,挑选完的样本继续留在原集合中。这样挑选m次来形成训练集。
- 训练集大小和已知数据集大小相同,但是训练集中有重复的数据,还有约0.368 * m的数据不会出现在训练集中,这个数字大家可以去看一下《机器学习》这本书。
- 训练集采用随机的方式选择样本,会改变原样本的分布情况,会产生一些偏差,适用于样本量较小的情况。
性能度量
错误率与精度
错误率比较好理解,对于 m m m个测试样本的测试机,如果有 e e e个样本分类错误,那么错误率就是 E = e / m E = e/m E=e/m。
精度就是 a c c = 1 − E acc = 1-E acc=1−E
光有错误率和精度是无法全面的评价一个学习算法的。
查准率 & 查全率
查准率的含义就是我预测出来的结果又多少是对的。
查全率的含义就是我预测出来的结果是不是全的。
从简单的问题看起,针对二分类问题,我们可以将最终预测的结果分成4个部分,大家仔细捋一捋,容易乱:
- 真正例(True Positive),TP。算法找到的,符合要求的样本。
- 假正例(False Positive),FP。算法找到的,但是不符合要求的样本。
- 真反例(True Negative),TN。算法找到的,但是实际不符合要求的样本。
- 假反例(False Negative),FN。算法没找到的,但是是符合要求的样本。
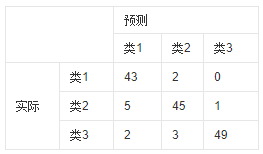
这里有一个概念可以引入:混淆矩阵。混淆矩阵就是一个 n ∗ n , n = 类 别 数 n * n, n = 类别数 n∗n,n=类别数的矩阵,混淆矩阵的每一列代表了预测类别,每一列的总数表示预测为该类别的数据的数目;每一行代表了数据的真实归属类别,每一行的数据总数表示该类别的数据实例的数目。
我们具体来他讨论二分类问题,那就是正例(符合要求)和反例(不符合要求)两种。
查准率就是说根据模型找出来的样本中,真正符合要求的有多少,毕竟有找错的(假正例)。所以查准率的计算方式为:
P = T P T P + F P P = \frac{TP}{TP+FP} P=TP+FPTP
查全率则是指根据模型找出来的样本中,符合要求的样本占全部符合要求的样本的比例,毕竟有漏掉的(假反例,就是算法判断这个样本不是符合要求的,实际上是符合要求的样本)。那么查全率的计算方式为:
R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP
查全率和查准率是相互制约的两个性能指标,查准率高意味着会把一些没那么有把握的样本排除掉(上一篇文章提到的,生成式模型会计算概率,根据概率和阈值进行分类,查准率提高的话就表示这个阈值定的比较高),那么可能就会把一些样本漏掉成为假反例,导致查全率降低。如果尽可能的把结果查全,表示这个阈值定的比较低,就会产生一些假正例,从而降低查准率。
那么一个算法来了,怎么平衡的,根据什么样的指导原则来选择呢?这就引出了P-R图和ROC图。
P-R图
P-R图的思路是,把算法模型给出的预测结果以样本为单位按概率高低进行排序,可能性最高的排最前面,最不可能的放最后面。然后按此顺序逐个把样本作为正例进行预测,再计算查全率与差准率 ( R , P ) (R,P) (R,P),把一系列的 ( R , P ) (R,P) (R,P)点标记在以查全率为横轴、查准率为纵轴的坐标里。
可以看出,随着查全率增加,查准率是下降的。
- 当P = R时,此时是比较平衡的策略
- 考察A/C两条曲线,A曲线的任何一个点的P, R都比C曲线的值要高,说明A曲线代表的算法完胜C曲线代表的算法
- 但是大部分情况是A/B两条曲线所描述的,在A/B两条曲线的交点右侧,在查准率相同的情况下,B曲线的查全率更优秀;在交点左边,在查全率相同的情况下,A曲线的查准率更优秀,所以就需要根据具体情况具体分析了。
- 如果非要综合比较,那么就是计算曲线与两根轴围住的区域面积,谁大谁的综合性能就更强。
那么怎么生成这个曲线呢,我们来举个栗子:
假设预测了十个样本,样本的概率如下,其中3号、5号、8号样本为反例:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 0.95 | 0.9 | 0.85 | 0.8 | 0.75 | 0.7 | 0.65 | 0.6 | 0.55 | 0.5 |
-
生成第一个点:把1号样本拿出来做正例,那么此时TP = 1,FP = 0,FN = 6(2,4,6,7,9,10均为假反例)。计算得出查准率P = 100%。而查全率只有1/7。
-
生成第二个点:把1号2号样本都作为正例,此时TP = 2,FP = 0,FN=5。计算得出查准率P = 100%。查全率为1/6。
-
生成第三个点:TP = 2,FP = 1,FN=5。计算得出查准率P = 2/3。查全率为2/7。
…
-
最后一个点:把所有的样本都算作正例,TP = 7, FP = 3,FN = 0。计算得出查准率P = 70%(最低),查全率为100%(最高)。
这个图就不画了,没有上面的图能说明问题。
ROC & AUC
对于二分类问题,ROC图还是通过TP/FP/TN/FN四个值来做计算,不过横轴换成假正例(FPR, False Positive Rate),纵轴是真正例率(TPR, True Positive Rate)。
T P R = T P T P + F N TPR = \frac{TP}{TP+FN} TPR=TP+FNTP
F P R = F P T N + F P FPR = \frac{FP}{TN+FP} FPR=TN+FPFP
通过这个计算公式,我们可以来理解一下这种统计方式的思想:
- TPR是想发现算法漏了哪一些样本,也就是被算法漏掉的、实际上是符合条件的那部分样本(FN)。如果是故障诊断算法的话,就是说算法判断是有故障的可行度有多高,也可以称之为真阳率。
- FPR是想发现算法错判断成符合条件的样本占整个不符合条件样本中的比例。如果是故障诊断算法的话,就是说算法认为是故障的话,实际上不是故障的概率有多大,称之为假阳率。
画ROC图的方式和P-R图的方式一样的,只是每次计算的值不一样而已,就不再举个栗子了。
-
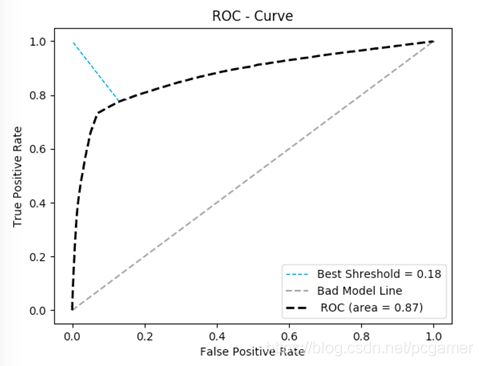
随着越来越多的样本加入到正例里,TPR会逐步增高,最理想的状况就是从原点顺着纵轴直接上去,也就是FPR持续为0。然后随着低概率的事件加入到正例里,顺着TPR=1.0的横轴达到右上角,也就是TPR一直为1。
-
而图中的Bad Model Line表示随着样本的逐步增加,TPR=FPR,也就是随机猜测,就是扔硬币,你的预测准确率只有50%一样。
-
一般来说,真实的曲线位于刚才说的两者之间,就像图中的黑色线。
-
曲线中最好的分界线(也就是阈值从哪个位置(哪个样本处,因为样本是按照顺序来构造这条ROC图))就是曲线的斜率小于45度的时候。因为从这个点开始,TPR增加率就开始低于FPR的增加率了。为了增加更多的TPR,需要增加更多额FPR作为代价。
AUC表示曲线下面覆盖的面积,可以表示这个算法的综合性能。
ROC和P-R图从不同的评价方向来评价一个算法的好坏,举一个极端的例子:一个二类分类问题一共10个样本,其中9个样本为正例,1个样本为负例,在全部判正的情况下准确率将高达90%,而这并不是我们希望的结果,尤其是在这个负例样本得分还是最高的情况下,模型的性能本应极差,从准确率上看却适得其反。而AUC能很好描述模型整体性能的高低。这种情况下,模型的AUC值将等于0,因为第一个点计算出来的TPR = 0,而FPR = 1,已经是最右边的那个点了。
代价敏感错误与代价曲线
在一些情况下,P-R图/ROC也没法很客观的评价一个学习算法。比如医疗相关的学习期,判断病人是否有某种疾病。FP的情况,也就是没病的误判成有病的情况,这种情况下,最多就是浪费病人的时间和金钱,重新做了一些检查。但是如果是FN的情况,也就是有病的判断成没病,这种情况就会耽误最佳治疗时间,最终可能导致生命危险。很明显,FP和FN的代价是不一样的,而P-R图和ROC图中没有对这个的评价。
为了把判断错误的代价考虑到性能度量里,我们可以把上面提到的混淆矩阵改造一下,矩阵中的数字是用于描述错误代价:
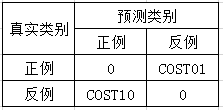
针对这个矩阵,定义了坐标的横轴与纵轴:
横轴:
P ( + ) c o s t = p ∗ c o s t 01 p ∗ c o s t 01 + ( 1 − p ) c o s t 10 ① P(+)cost=\frac{p*cost_{01}}{p*cost_{01}+(1-p)cost_{10}} ① P(+)cost=p∗cost01+(1−p)cost10p∗cost01①
p p p是表示样本中正例的概率,拿ROC中的那个例子来说, p = 0.7 p=0.7 p=0.7
所以这个公式本质上可以看成就是正例的概率 p p p本身,比如在没有代价的计算中, c o s t 01 = c o s t ( 10 ) cost_{01} = cost_(10) cost01=cost(10),那么这个公式就退化成 P ( + ) c o s t = p P(+)cost = p P(+)cost=p。假设正例被判断成反例的后果更严重一点,也就是 c o s t 01 > c o s t 10 cost_{01} > cost_{10} cost01>cost10,在上例中, p > 0.7 p>0.7 p>0.7;反之, p < 0.7 p<0.7 p<0.7。
我们再看下纵轴的定义:
c o s t n o r m = F N R ∗ p ∗ c o s t 01 + F P R ∗ ( 1 − p ) ∗ c o s t 10 p ∗ c o s t 01 + ( 1 − p ) c o s t 10 ② cost_{norm} = \frac{FNR*p*cost{01} + FPR*(1-p)*cost{10}}{p*cost_{01}+(1-p)cost_{10}} ② costnorm=p∗cost01+(1−p)cost10FNR∗p∗cost01+FPR∗(1−p)∗cost10②
将②式进行一下变形:
c o s t n o r m = F N R ∗ p ∗ c o s t 01 p ∗ c o s t 01 + ( 1 − p ) c o s t 10 + F P R ∗ ( 1 − p ) ∗ c o s t 10 p ∗ c o s t 01 + ( 1 − p ) c o s t 10 cost_{norm} = \frac{FNR*p*cost{01}}{p*cost_{01}+(1-p)cost_{10}} + \frac{FPR*(1-p)*cost{10}}{p*cost_{01}+(1-p)cost_{10}} costnorm=p∗cost01+(1−p)cost10FNR∗p∗cost01+p∗cost01+(1−p)cost10FPR∗(1−p)∗cost10
c o s t n o r m = F N R ∗ P ( + ) c o s t + F P R ∗ ( 1 − p ) ∗ c o s t 10 p ∗ c o s t 01 + ( 1 − p ) c o s t 10 ③ cost_{norm} = FNR*P(+)cost + \frac{FPR*(1-p)*cost{10}}{p*cost_{01}+(1-p)cost_{10}} ③ costnorm=FNR∗P(+)cost+p∗cost01+(1−p)cost10FPR∗(1−p)∗cost10③
再看公式:
1 − P ( + ) c o s t = ( 1 − p ) c o s t 10 p ∗ c o s t 01 + ( 1 − p ) c o s t 10 1-P(+)cost =\frac{(1-p)cost_{10}}{p*cost_{01}+(1-p)cost_{10}} 1−P(+)cost=p∗cost01+(1−p)cost10(1−p)cost10
所以公式③可以变化为:
c o s t n o r m = F N R ∗ P ( + ) c o s t + F P R ∗ ( 1 − P ( + ) c o s t ) ④ cost_{norm} = FNR*P(+)cost + FPR*(1-P(+)cost) ④ costnorm=FNR∗P(+)cost+FPR∗(1−P(+)cost)④
其中,FNR表示假阴率,也就是正例被错判为反例的样本情况。FPR是假阳率,也就是反例被错判为正例的样本情况。
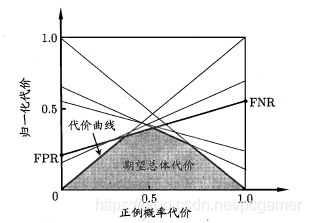
有了上面的公式,我们来看一下这个图是怎么画出来的:
-
首先考察下 ( 0 , F P R ) (0,FPR) (0,FPR), ( 1 , F N R ) (1,FNR) (1,FNR)这条线段。要搞明白这个线段是怎么出来的,我们将公式④再做一个小变换:
c o s t n o r m = ( F N R − F P R ) P ( + ) c o s t + F P R ⑤ cost_{norm} = (FNR-FPR)P(+)cost + FPR ⑤ costnorm=(FNR−FPR)P(+)cost+FPR⑤
上面说过了, P ( + ) c o s t P(+)cost P(+)cost为横轴,我们把它看成自变量 x x x, F N R − F P R FNR-FPR FNR−FPR看成参数 a a a,那么公式⑤就成了
c o s t n o r m = a x + F P R cost_{norm} = ax + FPR costnorm=ax+FPR
这个公式在坐标系中就是表示了一条直线,那么:
x = 0 , c o s t n o r m = F P R x = 0, cost_{norm} = FPR x=0,costnorm=FPRx = 1 , c o s t n o r m = F N R x = 1, cost_{norm} = FNR x=1,costnorm=FNR
这就是 ( 0 , F P R ) (0,FPR) (0,FPR), ( 1 , F N R ) (1,FNR) (1,FNR)线段。
-
上面提到了, P ( + ) c o s t P(+)cost P(+)cost可以简单等于样本正例概率 p p p,在含代价信息的语义下,就是正例的重要程度。我们再来看一下这个 c o s t n o r m cost_{norm} costnorm是个什么含义。看一下公式4:其中第一项 F N R ∗ P ( + ) c o s t FNR*P(+)cost FNR∗P(+)cost,FNR表示正例误判成反例的概率,所以 F N R ∗ P ( + ) c o s t FNR*P(+)cost FNR∗P(+)cost就表示正例误判成反例的影响程度;而 F P R ∗ ( 1 − P ( + ) c o s t ) FPR*(1-P(+)cost) FPR∗(1−P(+)cost)就表示反例误判成正例的影响程度。
所以,纵轴的数字就表示两者的影响程度相加,线段上的一个点的含义就是在某个样本正例的比例下, 学习期的误判影响程度。而整个线段的含义就是,随着样本正例的比例增加,影响程度的走向。
-
前面讲ROC的时候,我们可以看出,如何对预测值进行阈值划分,会影响到FPR,FNR,TPR,TNR这四个值,在ROC中,对应的就是图中的一个一个的点。而在代价曲线中,就是不同的线段,参考第一条,FPR,FNR变了,起点和都会发生变化。
-
在上面一点中提到,在划分正例/反例的阈值变化时,代价曲线图中会增加一条。那么,我们看一下,当正例概率一定的情况下,阈值划分造成的若干条线段的区别:
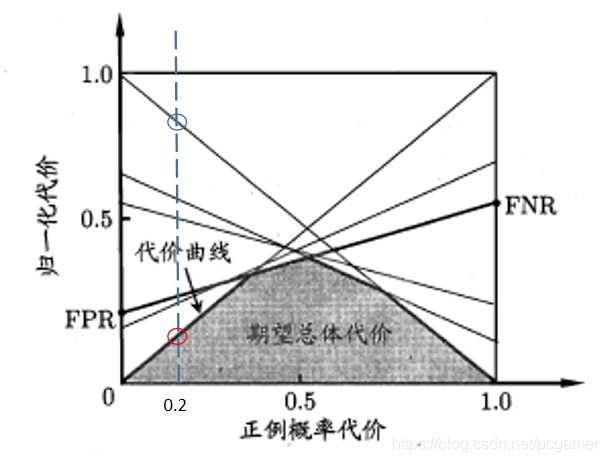
也就是说,在样本正例比例 p = 0.2 p=0.2 p=0.2时(这里先假定 P ( + ) c o s t ≈ p P(+)cost\approx p P(+)cost≈p),红圈圈出的交叉点代表的那条直线(划分阈值 α \alpha α)的代价最小,蓝圈代表的那条直线(划分阈值 β \beta β)代价最大。而我们的目标是要找出代价最低的,那么此时,我们选择红圈所代表的阈值: α \alpha α
再看一下当 p = 0.8 p=0.8 p=0.8时的情况:
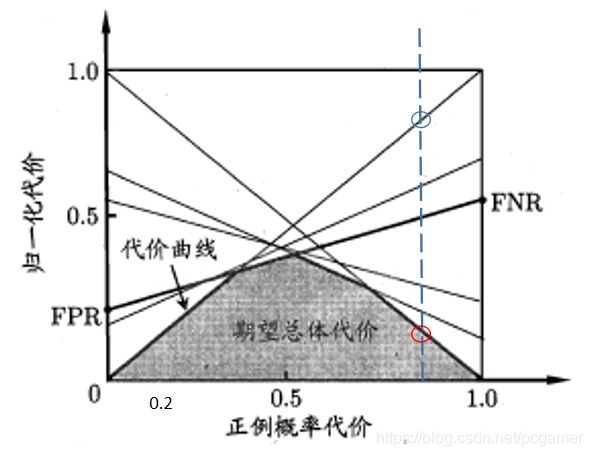
可以看出,红圈代表的曲线是上面提到阈值 β \beta β。所以,阴影部分代表的含义,我的理解是当正例比例变化时,在各个阈值中取最小的线段所围成的区域。
-
我们再看一下 P ( + ) c o s t ≠ p P(+)cost\neq p P(+)cost=p的情况,假设正例判盼成反例的的代价 c o s t 01 > c o s t 10 cost_{01} > cost_{10} cost01>cost10,那么 ( 0 , F P R ) (0, FPR) (0,FPR), ( 0 , F N R ) (0,FNR) (0,FNR)的曲线会更加向左陡峭一点(如下图中的虚线,表示全部反例判成正例的代价会小,看 ( 0 , F P R ) (0,FPR) (0,FPR)这个点,也就是说此时没有正例样本,此时反例判成正例的成本是低于原来的那条曲线的):
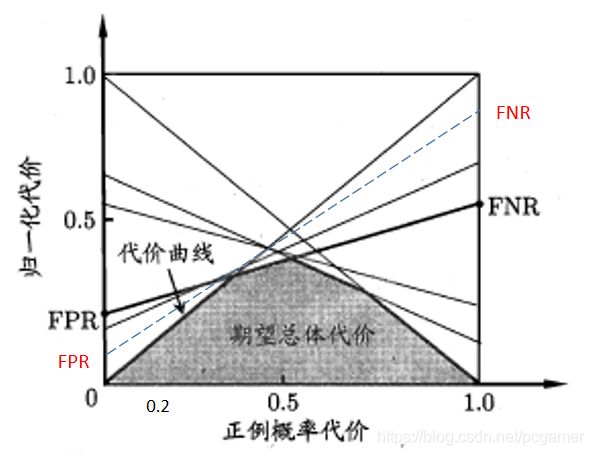
如果是 c o s t 01 < c o s t 10 cost_{01} < cost_{10} cost01<cost10: