异常值检测方法汇总

前言

首先这不是一篇简单探究算法的文章，本文是从项目的角度出发来探究如何对数据进行异常值检测，重点是机器学习算法（针对有异常和无异常的各种情况），当然后面还会包括一些模型部署、产品上线的内容。

具体算法使用代码，见我的GitHub
。

一、项目流程

1.目标确立

要开始一个项目，首先就得明确一个目的，根据这个目的从而思考一下几个问题：

1. 做什么？
2. 为什么要做？
3. 谁来做？
4. 什么时候做？
5. 怎么做？
6. 优势在哪？

当然你或许考虑的更多，不光是技术，还有人力、成本、利润、营销等问题。但是一般这个不是你该考虑的问题，除非你就是项目经理。.

就拿本文来说，检测离群点或异常值是数据挖掘的核心问题之一。数据的爆发和持续增长以及物联网设备的传播，使我们重新思考处理异常的方式以及通过观察这些异常来构建的应用场景。

举个简单的例子：

我们现在可以通过智能手表和手环每几分钟检测一次心率。检测心率数据中的异常可以帮助预测心脏疾病。交通模式中的异常检测可以帮助预测事故。异常检测还可用于识别网络基础设施和服务器间通信的瓶颈。因此，基于异常检测构建的使用场景和解决方案是无限的。

2.数据准备

由于此次的数据是敏感数据源，所以不能公开展示，这里只是简单的描述一下数据如何准备。

一般数据的准备主要有以下几种方式：

1. 数据库数据
2. 由统计、调查、报告获得 CSV、Excel等文件型数据
3. 网络爬虫数据
4. 某些开放型平台数据

3.数据分析处理

数据处理分析详见前面写的这两篇文章：

Pandas数据处理与分析

数据预处理（sklearn.preprocessing）

数据分析处理没有固定的方法，仁者见仁智者见智，根据自己数据的形式和存在问题进行分析处理。

4.模型算法（重点）

进行异常值检测的方法有很多，主要的话有以下几种大的分类：

1. 传统统计方法
2. 机器学习方法
3. 深度学习方法
4. 其他方法

4.1 传统统计方法

在统计学中，离群点是并不属于特定族群的数据点，是与其它值相距甚远的异常观测。离群点是一种与其它结构良好的数据不同的观测值。

4.1.1 3σ准则

3σ准则是指先假设一组检测数据只含有随机误差，对其进行计算处理得到标准偏差，按一定概率确定一个区间，认为凡超过这个区间的误差，就不属于随机误差而是粗大误差，含有该误差的数据应予以剔除。

这种判别处理原理及方法仅局限于对正态或近似正态分布的样本数据处理，它是以测量次数充分大为前提（样本>10），当测量次数少的情形用准则剔除粗大误差是不够可靠的。
3σ法则为：

• 数值分布在（μ-σ,μ+σ)中的概率为0.6827
• 数值分布在（μ-2σ,μ+2σ)中的概率为0.9545
• 数值分布在（μ-3σ,μ+3σ)中的概率为0.9973

可以认为，Y 的取值几乎全部集中在（μ-3σ,μ+3σ)区间内，超出这个范围的可能性仅占不到0.3%

因此，如果你有任何数据点超过标准差的 3 倍，那么这些点很有可能是异常值或离群点。(正态分布)

算法实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
np.random.seed(42)
anomalies = []
normal = []
# 生成一些数据
data = np.random.randn(50000)  * 20 + 20

# 在一维数据集上检测离群点的函数
def find_anomalies(random_data):
    # 将上、下限设为3倍标准差
    random_data_std = np.std(random_data)
    random_data_mean = np.mean(random_data)
    anomaly_cut_off = random_data_std * 3

    lower_limit  = random_data_mean - anomaly_cut_off 
    upper_limit = random_data_mean + anomaly_cut_off
    print("下限： ",lower_limit)
    print("上限： ",upper_limit)
    # 异常
    for outlier in random_data:
        if outlier > upper_limit or outlier < lower_limit:
            anomalies.append(outlier)
        else:
            normal.append(outlier)
    return pd.DataFrame(anomalies,columns=["异常值"]),pd.DataFrame(normal,columns=["正常值"])

anomalies,normal = find_anomalies(data)

这段代码的输出是一组大于 80 或小于-40 的异常值和正常值。注意，输入的数据集是正态分布的并且是一维的。

4.1.2 四分位（箱线图）

箱形图是数字数据通过其四分位数形成的图形化描述。这是一种非常简单但有效的可视化离群点的方法。考虑把上下触须作为数据分布的边界。任何高于上触须或低于下触须的数据点都可以认为是离群点或异常值

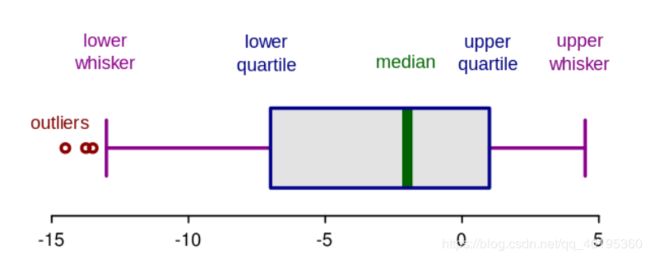
四分位间距 (IQR) 的概念被用于构建箱形图。IQR 是统计学中的一个概念，通过将数据集分成四分位来衡量统计分散度和数据可变性。简单来说，任何数据集或任意一组观测值都可以根据数据的值以及它们与整个数据集的比较情况被划分为四个确定的间隔。四分位数会将数据分为三个点和四个区间。

四分位间距对定义离群点非常重要。它是第三个四分位数和第一个四分位数的差 (IQR = Q3 -Q1)。在这种情况下，离群点被定义为低于箱形图下触须（或 Q1 − 1.5x IQR）或高于箱形图上触须（或 Q3 + 1.5x IQR）的观测值。

算法实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
np.random.seed(42)
anomalies = []
normal = []
# 生成一些数据
data = np.random.randn(50000)  * 20 + 20

# 在一维数据集上检测离群点的函数
def find_anomalies(random_data):
    # 将上、下限设为3倍标准差
    iqr_25 = np.percentile(random_data, [25])
    iqr_75 = np.percentile(random_data, [75])

    lower_limit  = iqr_25 - 1.5 * (iqr_75 - iqr_25) 
    upper_limit = iqr_25 + 1.5 * (iqr_75 - iqr_25)
    print("下限： ",lower_limit)
    print("上限： ",upper_limit)
    # 异常
    for outlier in random_data:
        if outlier > upper_limit or outlier < lower_limit:
            anomalies.append(outlier)
        else:
            normal.append(outlier)
    return pd.DataFrame(anomalies,columns=["异常值"]),pd.DataFrame(normal,columns=["正常值"])

anomalies,normal = find_anomalies(data)

优点：与方差和极差相比，更加不如意受极端值的影响，且处理大规模数据效果很好。

缺点：小规模处理略显粗糙。而且只适合单个属相的检测。

除以上两种简单的基于统计学的异常值检测方法之外，还有诸如：卡方检验、方差分析等方法，有兴趣可以自己尝试代码。

4.2 机器学习方法（重点）

机器学习方法可以分为以下几类：

1. 有标签的监督学习
2. 无标签的无监督学习

4.2.1 监督学习算法

监督学习的算法适用于正常数据和异常数据都存在且有标签的情况下。这种假设情况是很完美的，因为他把异常值检测就转化成了分类算法，有众多的机器学习算法可以使用。

或许你在思考这样一个问题：如果异常值很少，正常值很多，样本不平衡怎么办？

对于这样一个问题，一般有两种解决办法：

1. 算法层面：有些算法内部会自动的带有使样本平衡参数，例如SVM中的class_weight = "balanced"。
2. 数据层面：从数据层面来说主要就是上采样和下采样，但一般推荐SMOTE算法生成样本量较少的数据。

常见的分类算法效果较好的有：

• KNN
• RF
• GBDT
• SVM
• XGBoost
• ……
  这些算法我就不去实现了，也没啥必要去实现，都是基本的分类算法。

4.2.2 无监督学习算法

无监督学习的算法适用于正常数据和异常数据都存在且没有标签的情况下，这种异常值检测也被称作为离群值检测。这类算法主要有：

• IsolationForest
• DBSCAN
• Local Outlier Factor（LOF）

IsolationForest

孤立森林（Isolation Forest）是一种高效的异常检测算法，它和随机森林类似，但每次选择划分属性和划分点（值）时都是随机的，而不是根据信息增益或者基尼指数来选择。在建树过程中，如果一些样本很快就到达了叶子节点（即叶子到根的距离d很短），那么就被认为很有可能是异常点。因为那些路径d比较短的样本，都是因为距离主要的样本点分布中心比较远的。也就是说，可以通过计算样本在所有树中的平均路径长度来寻找异常点。

sklearn提供了ensemble.IsolationForest模块可用于Isolation Forest算法：

sklearn.ensemble.IsolationForest(n_estimators=100, max_samples='auto', contamination='auto', max_features=1.0, bootstrap=False, n_jobs=None, behaviour='deprecated', random_state=None, verbose=0, warm_start=False)

DBSCAN

DBSCAN 是一种用于把数据聚成组的聚类算法。它同样也被用于单维或多维数据的基于密度的异常检测。虽然其它聚类算法比如 k 均值和层次聚类也可用于检测离群点。但是DBSCAN效果较好，所以往往用它。

DBSCAN是基于密度的聚类算法,重点是发现邻居的密度(MinPts)在n维球体的半径ɛ。

DBSCAN定义不同类型的点：

• 核心点：A是一个核心的区域(ɛ所定义的)包含至少比参数MinPts同样多或更多的点。
• 边界点：C是一个位于集群中的边界点，它的邻域并不包含比MinPts更多的点，但它仍然是集群中其他点的“密度可达”。
• 离群点：N是一个离群点，在没有集群的情况下，它不是“密度可达”或“密度连接”到任何其他点。因此，这一点将有“他自己的集群”。

DBSVAN对MinPts参数也很敏感，它将完全依赖于手动调整的问题，其复杂度为O(n log n)，它是一种具有中等大小的数据集的有效方法，我们可以使用Scikit-learn来实现：

sklearn.cluster.DBSCAN(eps=0.5, min_samples=5, metric='euclidean', metric_params=None, algorithm='auto', leaf_size=30, p=None, n_jobs=None)

DBSCAN 优点：

• 当特征空间中的值分布不是假设的时，这是一种非常有效的方法。

• 如果搜索异常值的特征空间是多维的(比如：3或更多的维度)，则可以很好地工作。

DBSCAN 缺点：

• 特征空间中的值需要相应地伸缩。

• 选择最优参数eps,MinPts和度规可能很困难，因为它对任何三个参数都非常敏感。

• 它是一个无监督的模型，需要在每次分析新的数据时重新校准。

Local Outlier Factor（LOF）

局部异常因子（LOF）算法是一个很特殊的异常检测算法，因为它既可以对数据进行无监督学习，还可以进行半监督学习。

首先讨论他的思想：每个样本的异常分数称为局部异常因子。它测量给定样本相对于其邻居的密度的局部偏差。它是局部的，异常得分取决于物体相对于周围邻域的隔离程度。更确切地说，局部性由k近邻给出，其距离用于估计局部密度。通过将样本的局部密度与其邻居的局部密度进行比较，可以识别密度明显低于其邻居的样本，这些被认为是异常值。

说白了就是，它计算给定数据点相对于其邻居的局部密度偏差。它将密度大大低于邻居的样本视为异常值。

之所以说LOF两种方法都支持取决于该算法中的一个参数：novelty = True则是半监督学习，novelty = False则是无监督学习。

sklearn.neighbors.LocalOutlierFactor(n_neighbors=20, algorithm='auto', leaf_size=30, metric='minkowski', p=2, metric_params=None, contamination='auto', novelty=False, n_jobs=None)

方法	离群点检测novelty = False	新奇点检测novelty = True
fit_predict	可用	不可用
predict	不可用	只能用于新数据
decision_function	不可用	只能用于新数据
score_samples	用 negative_outlier_factor_	只能用于新数据

4.2.3 半监督学习算法

半监督学习的算法适用于只有正常数据，没有异常数据的情况下，这种异常值检测也被称作为新奇点检测。这类算法主要有：

• Local Outlier Factor（LOF）
• One-Class SVM

Local Outlier Factor（LOF）

上面已经讨论过，这里不再讨论。

One-Class SVM

在介绍One-Class SVM之前，你知道他代表什么意思吗？

如果将分类算法进行划分，根据类别个数的不同可以分为单分类，二分类，多分类。常见的分类算法主要解决二分类和多分类问题，预测一封邮件是否是垃圾邮件是一个典型的二分类问题，手写体识别是一个典型的多分类问题，这些算法并不能很好的应用在单分类上。那么为什么又要去研究单分类呢？

单分类问题在工业界广泛存在，由于每个企业刻画用户的数据都是有限的，很多二分类问题很难找到负样本，即使用一些排除法筛选出负样本，负样本也会不纯，不能保证负样本中没有正样本。所以在只能定义正样本不能定义负样本的场景中，使用单分类算法更合适。单分类算法只关注与样本的相似或者匹配程度，对于未知的部分不妄下结论。

OneClassClassification中的训练样本只有一类，因此训练出的分类器将不属于该类的所有其他样本判别为“不是”即可，而不是由于属于另一类才返回“不是”的结果。

One Class SVM也是属于支持向量机大家族的，但是它和传统的基于监督学习的分类回归支持向量机不同，它是无监督学习的方法，也就是说，它不需要我们标记训练集的输出标签。那么没有类别标签，我们如何寻找划分的超平面以及寻找支持向量机呢？One Class SVM这个问题的解决思路有很多。这里只讲解一种特别的思想SVDD，对于SVDD来说，我们期望所有不是异常的样本都是正类别，同时它采用一个超球体而不是一个超平面来做划分，该算法在特征空间中获得数据周围的球形边界，期望最小化这个超球体的体积，从而最小化异常点数据的影响。

sklearn.svm.OneClassSVM(kernel='rbf', degree=3, gamma='scale', coef0=0.0, tol=0.001, nu=0.5, shrinking=True, cache_size=200, verbose=False, max_iter=-1)

4.3 深度学习方法

前面重点介绍了关于机器学习的异常检测，其实深度学习里面也有很多关于异常检测的思想，但是实现起来就比使用sklearn难太多。不过说到这里也简单介绍几个我使用Pytorch实现在异常值检测吧。

1. AE（AutoEncoder）
2. VAE（Variational Autoencoder）
3. GAN

4.3.1 AE（AutoEncoder）

Autoencoder，中文称作自编码器，是一种无监督式学习模型。本质上它使用了一个神经网络来产生一个高维输入的低维表示。Autoencoder与主成分分析PCA类似，但是Autoencoder在使用非线性激活函数时克服了PCA线性的限制。

Autoencoder包含两个主要的部分，encoder（编码器）和 decoder（解码器）。Encoder的作用是用来发现给定数据的压缩表示，decoder是用来重建原始输入。在训练时，decoder 强迫 autoencoder 选择最有信息量的特征，最终保存在压缩表示中。最终压缩后的表示就在中间的coder层当中。以下图为例，原始数据的维度是10，encoder和decoder分别有两层，中间的coder共有3个节点，也就是说原始数据被降到了只有3维。Decoder根据降维后的数据再重建原始数据，重新得到10维的输出。从Input到Ouptut的这个过程中，autoencoder实际上也起到了降噪的作用。

AutoEncoder无监督异常检测

在无监督的情况下，我们没有异常样本用来学习，而算法的基本上假设是异常点服从不同的分布。根据正常数据训练出来的Autoencoder，能够将正常样本重建还原，但是却无法将异于正常分布的数据点较好地还原，基于AE的重构损失导致还原误差较大。

如果样本的特征都是数值变量，我们可以用MSE或者MAE作为还原误差。

4.3.2 VAE（Variational AutoEncoder(VAE)）

接下来介绍一些VAE模型，对于VAE模型的基本思想，下面内容主要引用自我觉得讲得比较清楚的一篇知乎文章，并根据我的理解将文中一些地方进行修改，保留核心部分，这里假设读者知道判别模型与生成模型的相关概念。
原文地址：https://zhuanlan.zhihu.com/p/27865705

VAE 跟传统 AutoEncoder关系并不大，只是思想及架构上也有 Encoder 和 Decoder 两个结构而已。VAE 理论涉及到的主要背景知识包括：隐变量（Latent Variable Models）、变分推理（Variational Inference）、Reparameterization Trick 等等。

下图表示了VAE整个过程。即首先通过Encoder 得到$x$的隐变量分布参数；然后采样得到隐变量 $z$ 。接下来按公式，应该是利用 Decoder 求得 $x$ 的分布参数，而实际中一般就直接利用隐变量恢复 $x$ 。

VAE也实现了跟AutoEncoder类似的作用，输入一个序列，得到一个隐变量（从隐变量的分布中采样得到），然后将隐变量重构成原始输入。不同的是，VAE学习到的是隐变量的分布(允许隐变量存在一定的噪声和随机性)，因此可以具有类似正则化防止过拟合的作用。

基于VAE的异常检测方法其实跟AutoEncoder基本一致，可以使用重构误差来判断异常。

缺陷

基于AutoEncoder和VAE模型在工业界上的使用面临的最大问题是：

需要设置异常阈值。因为我们检测异常是通过对比重构后的结果与原始输入的差距，而这个差距多少就算是异常需要人为定义，然而对于大量的不同类型的数据，我们很难去统一设置阈值，这也是采用VAE模型比较大的一个缺陷。虽然在Dount论文中，采用的是重构概率而不是重构误差来判断异常，然而重构概率也需要设置阈值才能得到比较精确的结果。

4.3.3 GAN

这里很难，后面有时间在更新。

4.4 其他方法

5.模型部署

这一部分是由flask来搭建平台的，后面会更新。具体代码可以看Github

6.维护更新