模糊C均值聚类算法---图像分割(python)
Fuzzy C-Means算法
模糊c均值聚类融合了模糊理论的精髓。相较于k-means的硬聚类,模糊c提供了更加灵活的聚类结果。因为大部分情况下,数据集中的对象不能划分成为明显分离的簇,指派一个对象到一个特定的簇有些生硬,也可能会出错。故,对每个对象和每个簇赋予一个权值,指明对象属于该簇的程度。当然,基于概率的方法也可以给出这样的权值,但是有时候我们很难确定一个合适的统计模型,因此使用具有自然地、非概率特性的模糊c均值就是一个比较好的选择。
算法原理
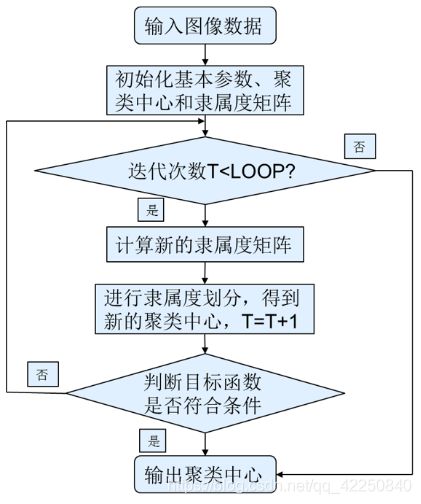
流程图
代码实现
- 初始聚类中心
c = 4 # 聚类数目c
b = 2 # b>l,是一个可以控制聚类结果的模糊程度的常数。
m=np.array([[0, 0, 0,],[0, 0, 0,], [0, 0, 0,], [0, 0, 0, ]]).astype(float)
- 计算隶属度
while(x>0.001):
for row in range(h):
for col in range(w):
temp=0
for i in range(c):
# 避免分母会为0,需要判断
if paradigm(img[row][col],m[i])!=0:
temp= temp + pow(1/paradigm(img[row][col],m[i]),1/(b - 1))
else:
temp = temp + pow(1/(10e-10),1/(b - 1))
for j in range(c):
# 避免分母会为0,需要判断
if paradigm(img[row][col],m[j]) != 0:
t=math.pow(1/paradigm(img[row][col],m[j]),1/(b-1))
else:
t=math.pow(1/(10e-10),1/(b-1))
# 更新隶属度表Mu
mu[row][col][j]=t/temp
- 更新聚类中心
# 按照公式,将m的分子分母部分分别计算出来
t=math.pow(mu[row][col][j],b)
for i in range(ch):
mfenzi[j][i]=mfenzi[j][i] + (t*img[row][col][i])
mfenmu[j]=mfenmu[j] + t
for i in range(c):
for j in range(ch):
m[i][j]=mfenzi[i][j]/mfenmu[i]
- 计算损失函数
# 按照公式,为计算损失度做准备
js[j]= js[j]+math.pow(mu[row][col][j],b)*paradigm(img[row][col],m[j])
# 初始本次的损失度
J1=0
# 根据之前的准备计算得到更新后的隶属度中心和损失度
for i in range(c):
for j in range(ch):
J1= J1 + js[i]
# 计算损失度的变化率,并为下一次计算做准备
x=(J1-J0)/J0
J0=J1
完整代码
import cv2 as cv
import numpy as np
import math
import sys
import matplotlib.pyplot as plt
sys.setrecursionlimit(10000000)
#设置print选项的参数,使输出不为科学计数法
np.set_printoptions(suppress=True)
#平方函数
def paradigm2(x):
return x*x
def paradigm(x,y):
sum = 0
for i in range(3):
sum = sum + (x[i]-y[i])*(x[i]-y[i])
# print(sum)
return sum
#以像素值为聚类数据
def updatecenter(img,m,J0): #m是指聚类中心,J0是初始的损失度
# 初始化损失度的变化率
x=J0
h,w,ch=img.shape
# 定义两个变量mfenzi、mfenmu,为计算更新后的聚类中心做准备
mfenzi = np.random.randint(0, 1, size=(c, ch)).astype(float)
mfenmu = np.arange(c).astype(float)
# 定义变量js,为计算聚类损失度做准备
js = np.arange(c) * 0.0
# mu:记录每一个点对每一个中心的隶属度值
mu = np.zeros([h, w, c], np.double)
while(x>0.001):
for row in range(h):
for col in range(w):
temp=0
for i in range(c):
# 避免分母会为0,需要判断
if paradigm(img[row][col],m[i])!=0:
temp= temp + pow(1/paradigm(img[row][col],m[i]),1/(b - 1))
else:
temp = temp + pow(1/(10e-10),1/(b - 1))
for j in range(c):
# 避免分母会为0,需要判断
if paradigm(img[row][col],m[j]) != 0:
t=math.pow(1/paradigm(img[row][col],m[j]),1/(b-1))
else:
t=math.pow(1/(10e-10),1/(b-1))
# 更新隶属度表Mu
mu[row][col][j]=t/temp
# 按照公式,将m的分子分母部分分别计算出来
t=math.pow(mu[row][col][j],b)
for i in range(ch):
mfenzi[j][i]=mfenzi[j][i] + (t*img[row][col][i])
mfenmu[j]=mfenmu[j] + t
# 按照公式,为计算损失度做准备
js[j]= js[j]+math.pow(mu[row][col][j],b)*paradigm(img[row][col],m[j])
# 初始本次的损失度
J1=0
# 根据之前的准备计算得到更新后的隶属度中心和损失度
for i in range(c):
for j in range(ch):
m[i][j]=mfenzi[i][j]/mfenmu[i]
J1= J1 + js[i]
# 计算损失度的变化率,并为下一次计算做准备
x=(J1-J0)/J0
J0=J1
# print(m,mu)
return m,mu
#标记矩阵
def sign(img,m,h,w,c):
count = 1
flag = np.zeros((h,w),dtype="int")
for z in range(c):
for i in range(h):
for j in range(w):
if all(img[i][j]==m[z]):
flag[i][j] = count
count += 1
return flag
#获得噪音位置
def noise_get(flag,h,w):
m = []
for i in range(1,h-1):
for j in range(1,w-1):
if flag[i-1][j-1]!=flag[i][j]:
if flag[i-1][j]!=flag[i][j]:
if flag[i-1][j+1]!=flag[i][j]:
if flag[i][j-1]!=flag[i][j]:
if flag[i][j+1]!=flag[i][j]:
if flag[i+1][j-1]!=flag[i][j]:
if flag[i+1][j]!=flag[i][j]:
if flag[i+1][j+1]!=flag[i][j]:
flag[i][j] = flag[i][j+1]
m.append([i,j])
return m
if __name__ == "__main__":
''''
① 设定聚类数目c和参数b;
② 初始化各个聚类中心mj;
③ 重复下面的运算,直到各个样本的隶属度值稳定:
ⅰ)用当前的聚类中心按式(4)计算隶属度函数;
ⅱ)用当前的隶属度函数按式(3)更新计算各类聚类中心。
'''''
# 打开图像
img = cv.imread('example.png')
h, w ,ch= img.shape
# 设定聚类数目c和参数b
c = 4 # 聚类数目c
b = 2 # b>l,是一个可以控制聚类结果的模糊程度的常数。
m=np.array([[0, 0, 0,],[0, 0, 0,], [0, 0, 0,], [0, 0, 0, ]]).astype(float)
#更新聚类中心
m,mu=updatecenter(img,m,1)
m=m.astype(np.uint8)
print("输出得到的聚类中心的RGB值:")
print(m)
#print(mu)
# 给不同类别的点以不同的像素值
img_new=img.copy()
for row in range(h):
for col in range(w):
for i in range(c):
# print(np.argmax(np.array(mu[row][col])))
img_new[row][col]=m[np.argmax(np.array(mu[row][col]))]
#print(img_new)
#初始化位置聚类中心
m_coordinate = np.array([[0,0],[0,0], [0,0], [0,0]]).astype(int)
for z in range(c):
x = m[z]
for i in range(h):
for j in range(w):
if all(x == img_new[i][j]):
m_coordinate[z] = [i,j]
else:
continue
print(m_coordinate)
#计算标记矩阵
flag = sign(img_new,m,h,w,c)
#print(flag)xz
noise_condition = noise_get(flag, h, w)
print(noise_condition)
for i in range(len(noise_condition)):
x = noise_condition[i][0]
y = noise_condition[i][1]
img_new[x][y] = img_new[x][y-1]
# 输出
plt.figure("PhotpProcess")
plt.subplot(1,2,1);img_x = img[:,:,[2,1,0]]
plt.imshow(img_x);plt.title('origin')
plt.subplot(1,2,2);img_x= img_new[:,:,[2,1,0]]
plt.imshow(img_x);plt.title('result')
plt.show()