leetcode 376. 摆动序列(三种解法)

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

示例 1:

输入: [1,7,4,9,2,5]
输出: 6
解释: 整个序列均为摆动序列。
示例 2:

输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。
示例 3:

输入: [1,2,3,4,5,6,7,8,9]
输出: 2

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/wiggle-subsequence
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

---

思路分析

思路一：

根据动态规划的思想，需要找准状态，可知，每一个数值处于两种状态，如3 - 4，此时4处于负值状态，5 - 4此时，4处于正值状态，那么我们需要有两个变量来存储。
并且由于题目的要求是求出最长的摆动序列，那么动态规划的状态转折表达式中设置两个状态数组，up[i],down[i]分别表示位置i前面（包括i）最长的摆动序列，即最大值，那么流思维导图：

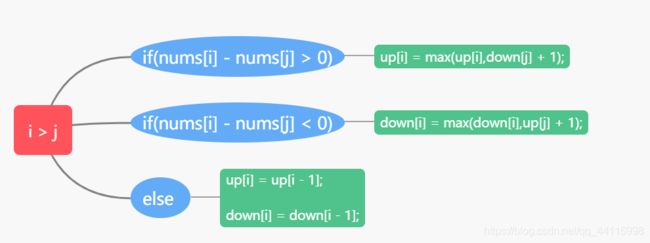
思路二：
在思路一的基础上，我们可知，既然已知每一个数处于的状态，如位置i的数，我们已知位置i前面所有的状态，，那么我们可以一次性遍历即可：

思路三：
在思路二的基础上，将空间缩小，因为我们发现每次参加运算的变量只有位置i和位置i - 1两个数，因为，可以直接用两个变量代替即可。

---

代码解析

思路一：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int size = nums.size();
        if(size == 0)
            return 0;
        int *up = new int[size + 1];
        int *down = new int[size + 1];
        memset(up,0,sizeof(up));
        memset(down,0,sizeof(down));
        up[0] = 1;
        down[0] = 1;
        for(int i = 1;i < size;++i){
            for(int j = 0;j < i;++j){
                if(nums[i] - nums[j] > 0)
                    up[i] = max(up[i],down[j] + 1);
                else if(nums[i] - nums[j] < 0)
                    down[i] = max(down[i],up[j] + 1);
                else {
                    up[i] = up[i - 1];
                    down[i] = down[i - 1];
                }
            }
        }
        return max(down[size - 1],up[size - 1]);
    }
};

思路二：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int size = nums.size();
        if(size == 0)
            return 0;
        int *up = new int[size + 1];
        int *down = new int[size + 1];
        memset(up,0,sizeof(up));
        memset(down,0,sizeof(down));
        up[0] = 1;
        down[0] = 1;
        for(int i = 1;i < size;++i){
            if(nums[i] - nums[i - 1] > 0){
                up[i] =down[i - 1] + 1;
                down[i] = down[i - 1];
            }
            else if(nums[i] - nums[i - 1] < 0){
                down[i] =up[i - 1] + 1;
                up[i] = up[i - 1];
            }
            else {
                up[i] = up[i - 1];
                down[i] = down[i - 1];
            }
        }
        return max(down[size - 1],up[size - 1]);
    }
};

并且思路二的优化方案,节省空间：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int size = nums.size();
        if(size == 0)
            return 0;
        int up = 1;
        int down = 1;
        for(int i = 1;i < size;++i){
            if(nums[i] - nums[i - 1] > 0)
                up =down + 1;
            else if(nums[i] - nums[i - 1] < 0)
                down =up + 1;
        }
        return max(down,up);
    }
};