DBSCAN算法简介及Python实现
DBSCAN算法简介与Python实现
第一次写博客,就挑了一篇数据挖掘课下实现的算法,尝试用自己的理解介绍清楚,参考教材是《数据挖掘概念与技术-第3版》。不当之处请大家指出。
-
- DBSCAN算法简介与Python实现
- 一、基本思想
- 二、代码实现
- 三、算法分析
- DBSCAN算法简介与Python实现
一、基本思想
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的空间聚类算法,直白翻译就是带有噪声应用的基于密度的空间聚类。
在了解DBSCAN算法前,先来学习一下密度聚类的几个常见概念:
- ϵ−邻域:以某个对象为中心、以ϵ为半径的空间; ϵ − 邻 域 : 以 某 个 对 象 为 中 心 、 以 ϵ 为 半 径 的 空 间 ;
- 核心对象ο:其领域稠密的对象,即该对象ϵ−领域内至少包括MinPts个对象; 核 心 对 象 ο : 其 领 域 稠 密 的 对 象 , 即 该 对 象 ϵ − 领 域 内 至 少 包 括 M i n P t s 个 对 象 ;
- 直接密度可达:对于核心对象q和对象p,如果p在q的ϵ−邻域内,则称p是从q直接密度可达; 直 接 密 度 可 达 : 对 于 核 心 对 象 q 和 对 象 p , 如 果 p 在 q 的 ϵ − 邻 域 内 , 则 称 p 是 从 q 直 接 密 度 可 达 ;
- 密度可达:如果存在一个对象链p1,p2...pn,使得p1=q,pn=p,并且对于在样本集中的pi,有pi+1是从pi关于ϵ和MinPts直接密度可达的,则p是从q密度可达。密度可达是非等价关系。 密 度 可 达 : 如 果 存 在 一 个 对 象 链 p 1 , p 2 . . . p n , 使 得 p 1 = q , p n = p , 并 且 对 于 在 样 本 集 中 的 p i , 有 p i + 1 是 从 p i 关 于 ϵ 和 M i n P t s 直 接 密 度 可 达 的 , 则 p 是 从 q 密 度 可 达 。 密 度 可 达 是 非 等 价 关 系 。
- 密度相连:如果样本中存在一个对象q,使得对象p1和对象p2都是从q关于ϵ和MinPts密度可达的,则对象p1,p2是密度相连的。密度相连是等价关系 密 度 相 连 : 如 果 样 本 中 存 在 一 个 对 象 q , 使 得 对 象 p 1 和 对 象 p 2 都 是 从 q 关 于 ϵ 和 M i n P t s 密 度 可 达 的 , 则 对 象 p 1 , p 2 是 密 度 相 连 的 。 密 度 相 连 是 等 价 关 系
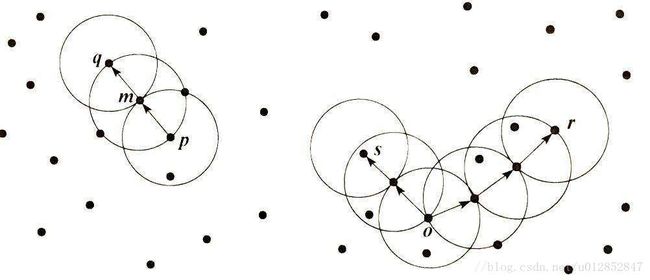
如图,m是核心对象,对象q在m的领域内,就说对象q是从核心对象m直接可达的。如果再有核心对象m是从核心对象p直接密度可达的,我们可得,对象q是从核心对象p密度可达。同样,对象s,r是密度相连的。
其中密度相连的闭包所标识的稠密区域作为簇。它也是密度聚类的可以发现任意形状簇的原因。
DBSCAN算法基本的思想其实很简单:
(1)DBSCAN通过检查数据集中每点的Eps邻域来搜索簇,如果点p的Eps邻域包含的点多于MinPts个,则创建一个以p为核心对象的簇;
(2)然后,DBSCAN迭代地聚集从这些核心对象直接密度可达的对象,这个过程可能涉及一些密度可达簇的合并;
(3)当没有新的点添加到任何簇时,该过程结束。
二、代码实现
伪代码:

用sklearn.datasets库中的方法,绘制了6000个二维样本点,如图:
Python实现如下:
from sklearn import datasets
import numpy as np
import random
import matplotlib.pyplot as plt
import time
def findNeighbor(j,X,eps):
N=[]
for p in range(X.shape[0]): #找到所有领域内对象
temp=np.sqrt(np.sum(np.square(X[j]-X[p]))) #欧氏距离
if(temp<=eps):
N.append(p)
return N
def dbscan(X,eps,min_Pts):
k=-1
NeighborPts=[] #array,某点领域内的对象
Ner_NeighborPts=[]
fil=[] #初始时已访问对象列表为空
gama=[x for x in range(len(X))] #初始时将所有点标记为未访问
cluster=[-1 for y in range(len(X))]
while len(gama)>0:
j=random.choice(gama)
gama.remove(j) #未访问列表中移除
fil.append(j) #添加入访问列表
NeighborPts=findNeighbor(j,X,eps)
if len(NeighborPts) < min_Pts:
cluster[j]=-1 #标记为噪声点
else:
k=k+1
cluster[j]=k
for i in NeighborPts:
if i not in fil:
gama.remove(i)
fil.append(i)
Ner_NeighborPts=findNeighbor(i,X,eps)
if len(Ner_NeighborPts) >= min_Pts:
for a in Ner_NeighborPts:
if a not in NeighborPts:
NeighborPts.append(a)
if (cluster[i]==-1):
cluster[i]=k
return cluster
X1, y1=datasets.make_circles(n_samples=5000, factor=.6,
noise=.05)
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2,1.2]], cluster_std=[[.1]],
random_state=9)
X = np.concatenate((X1, X2))
eps=0.08
min_Pts=10
begin=time.time()
C=dbscan(X,eps,min_Pts)
end=time.time()
plt.figure(figsize=(12, 9), dpi=80)
plt.scatter(X[:,0],X[:,1],c=C)
plt.show()
print "my dbscan用时:",end-begin结果如图:
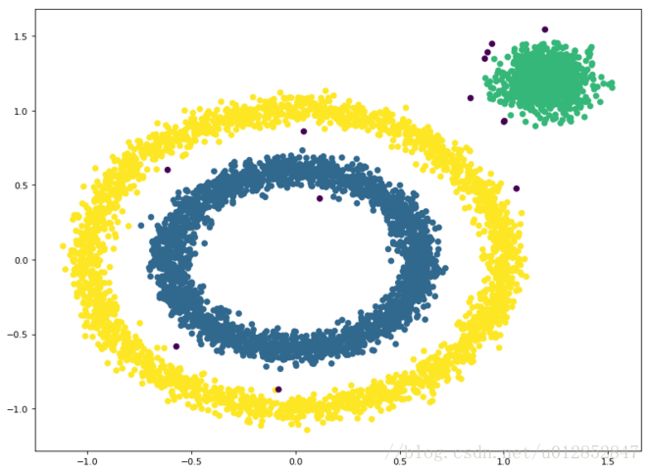
算法的时间复杂度是 O(N2),使用kd树减少对象之间计算距离的次数。将时间复杂度降为O(NlogN) O ( N 2 ) , 使 用 k d 树 减 少 对 象 之 间 计 算 距 离 的 次 数 。 将 时 间 复 杂 度 降 为 O ( N l o g N )
代码部分稍作修改:
kd=KDTree(X) #构建KD树
#NeighborPts:一维array,计算第j个样本的领域列表
NeighborPts=kd.query_ball_point(X[j],eps)在此简单介绍下kd树。kd树的主要思想跟二叉树类似,我们先来回忆一下二叉树的结构,二叉树中每个节点可以看成是一个数,当前节点总是比左子树中每个节点大,比右子树中每个节点小。
而KD树中每个节点是一个向量(也可能是多个向量),和二叉树总是按照数的大小划分不同的是,KD树每层需要选定向量中的某一维,然后根据这一维按左小右大的方式划分数据。在构建KD树时,关键需要解决2个问题:
(1)选择向量的哪一维进行划分(2)如何划分数据。第一个问题简单的解决方法可以是选择随机选择某一维或按顺序选择,但是更好的方法应该是在数据比较分散的那一维进行划分(分散的程度可以根据方差来衡量)。好的划分方法可以使构建的树比较平衡,可以每次选择中位数来进行划分,这样问题2也得到了解决。
三、算法分析
为了便于更好的视觉效果,我更改了数据集,采用datasets中的load_iris鸢尾花是数据集。
from sklearn.datasets import load_iris
#导入数据集
X=load_iris().data
#可视化部分
plt.scatter(iris['PetalLengthCm'],iris['PetalWidthCm'],c=cluster)
plt.show()设置不同参数,得到不同聚类结果:
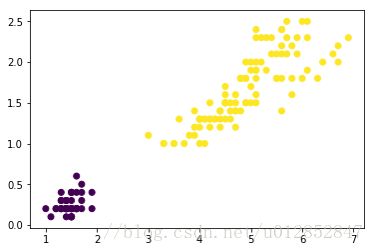
eps=0.9,MinPts=10
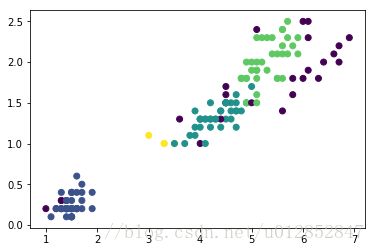
eps=0.3,MinPts=4
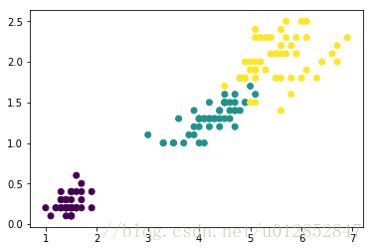
真实的鸢尾花数据分类如上图。通过比较可得如下结论:
- DBSCAN不需要事先知道要形成的簇类的数量,通过参数自动得到簇数;
- DBSCAN能够识别出噪声点。对离群点有较好的鲁棒性,甚至可以检测离群点;
- .输入参数敏感,确定参数Eps , MinPts困难 ,若选取不当 ,将造成聚类质量下降;
- 由于经典的DBSCAN算法中参数Eps和MinPts(全局性表征密度的参数)在聚类过程中是不变的,因此当各个类的密度不均匀,或类间的距离相差很大时,聚类的质量较差。