Matlab中快速傅里叶变换物理意义学习
本文参考了文章,一步步对一个标准信号进行分析,然后得到信号的幅度、频谱、相位信息。
一、基本概念
FFT
FFT(Fast Fourier Transformation)为一阶快速傅里叶变换,在数字信号处理中有着广泛的应用。有些信号在时域很难看到变化特征,在频域就很容易看得到,比如音符、线性调频信号。
FFT把时域信号变换到频谱上,直观的看出各频率信号的强弱。

采样得到的数字信号,就可以做FFT变换了。N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。做FFT分析时,幅值大小与FFT选择的点数有关,但是不影响分析结果。
由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
奈奎斯特采样定理
一个模拟信号,经过ADC采样之后,就变成了数字信号。采样定理告诉我们,采样频率要大于信号频率的两倍。
幅值和相位
假设采样频率为Fs,信号频率F,采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。
假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量,它的模值就是直流分量的N倍。而每个点的相位呢,就是在该频率下的信号的相位。
某点n所表示的频率为:Fn=(n-1)*Fs/N。
频谱分辨率
频率分辨率为:采样频率/采样点数=Fs/N。如果要提高频率分辨率,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
二、MATLAB实现
假设有一个信号由如下三个分量组成:
1)一个2V的直流分量;
2)一个频率为50Hz、相位为-30度、幅度为3V的交流信号;
3)一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。
其数学表达如下:
S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)
式中cos参数为弧度,所以-30度和90度要分别换算成弧度。
clc;
clear all;
close all;
% 假设有一个信号由如下三个分量组成:
% 1)一个2V的直流分量;
% 2)一个频率为50Hz、相位为-30度、幅度为3V的交流信号;
% 3)一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。
Fs = 256; % Sampling frequency
T = 1/Fs; % Sampling period
N = 256; % Length of signal
t = (0:N-1)*T; % Time vector
%cos参数为弧度,所以-30度和90度要分别换算成弧度。
S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180);
figure()
plot(S);
title('原始信号');
X = fft(S,N) %FFT变换 重点关注 第1点、第51点、和第76点附近有较大值
AX = abs(X)
figure()
plot(AX);
title('FFT模值');
Z = (fftshift(X))
figure()
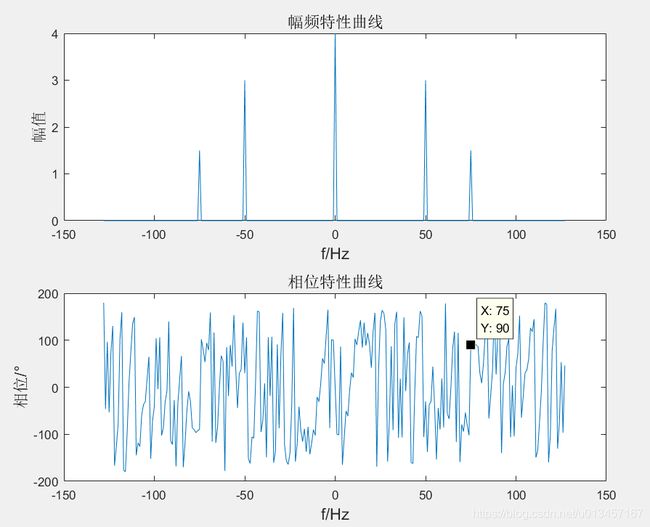
subplot(2,1,1);%二行一列第一幅图
plot((-N/2:N/2-1)*Fs/N,abs(Z)*2/N);%实际频率 实际幅值 计算*2/N (直流分量其实不需要*2)
title('幅频特性曲线','fontsize',13);
xlabel('f/Hz','fontsize',13);%横坐标显示f/Hz
ylabel('幅值','fontsize',13);%纵坐标显示幅值
subplot(2,1,2);%二行一列第二幅图
PX = angle(fftshift(X))*180/pi;
plot((-N/2:N/2-1)*Fs/N,PX);
title('相位特性曲线','fontsize',13);%显示标题
xlabel('f/Hz','fontsize',13);%横坐标显示f/Hz
ylabel('相位/°','fontsize',13);%纵坐标显示相位/°
三、物理意义分析
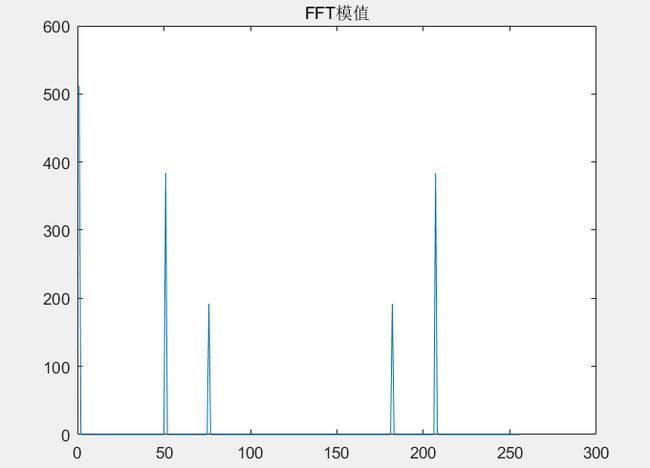
假设以256Hz的采样率对这个信号进行采样,总共采样256点。由前面的分析,Fn=(n-1)*Fs/N,可知:每两个点之间的间距为1Hz,第n个点的频率就是n-1。信号S有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,其它各点应该接近0。实际情况如何呢?我们来看看FFT的结果的模值如图所示。
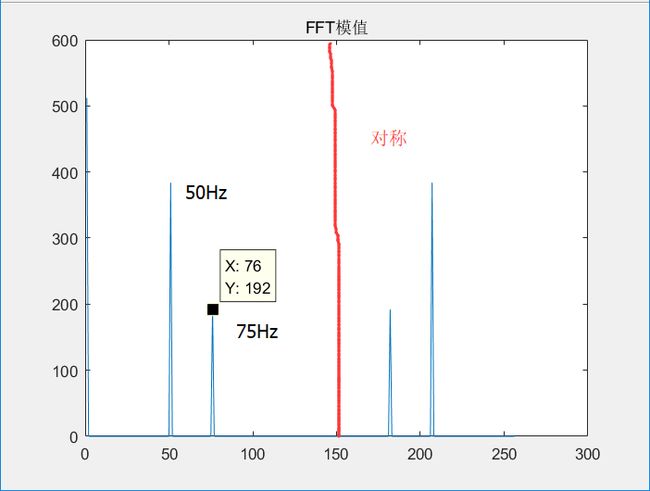
打印出这三个点附近的fft复数值:
X = fft(S,N) %FFT变换 重点关注 第1点、第51点、和第76点附近有较大值
| X | 模值 | |
|---|---|---|
| 第1个点 | 51200 + 0.0000i | 512.0000 |
| 第2个点 | -0.0000 - 0.0000i | 0.0000 |
| 第3个点 | -0.0000 - 0.0000i | 0.0000 |
| 第50个点 | -0.0000 - 0.0000i | 0.0000 |
| 第51个点 | 332.55 - 192.00i | 384.0000 |
| 第52个点 | -0.0000 - 0.0000i | 0.0000 |
| 第75个点 | -0.0000 - 0.0000i | 0.0000 |
| 第76个点 | 0.0000 + 192.00i | 192.0000 |
| 第77个点 | -0.0000 + 0.0000i | 0.0000 |
幅度分析
很明显,1点、51点、76点的值都比较大,它附近的点值都很小,可以认为是0,即在那些频率点上的信号幅度为0。
接着,我们来计算各点的幅度值。
由定理可知,给定模值An,
对于n!=1点的非直流信号它对应的幅度为:An/(N/2)
对于n=1点的信号,是直流分量,幅度即为An/N
因此,直流分量为:512/N=512/256=2;50Hz信号的幅度为:384/(N/2)=384/(256/2)=3;75Hz信号的幅度为192/(N/2)=192/(256/2)=1.5。可见,从频谱分析出来的幅度是正确的。
相位分析
相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi到pi。
然后再来计算相位信息。直流信号没有相位可言,不用管它。先计算50Hz信号的相位,atan2(-192, 332.55)=-0.5236,结果是弧度,换算为角度就是180*(-0.5236)/pi=-30.0001。再计算75Hz信号的相位,atan2(192,3.4386e-12)=1.5708弧度,换算成角度就是180*1.5708/pi=90.0002。可见,相位也是对的。
总结:假设采样频率为Fs,采样点数为N,做FFT之后,某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以N/2就是对应该频率下的信号的幅度(对于直流信号是除以N);该点的相位即是对应该频率下的信号的相位。