Leetcode 994. Rotting Oranges

994. Rotting Oranges

In a given grid, each cell can have one of three values:

the value 0 representing an empty cell;
the value 1 representing a fresh orange;
the value 2 representing a rotten orange.
Every minute, any fresh orange that is adjacent (4-directionally) to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1 instead.

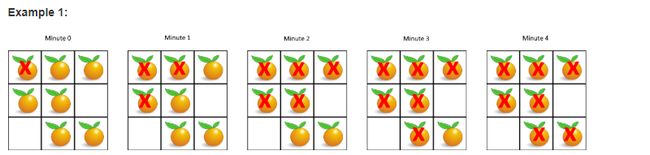
Input: [[2,1,1],[1,1,0],[0,1,1]]
Output: 4
Example 2:

Input: [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Example 3:

Input: [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

题意 ：就是有个棋盘，然后里面可能有坏的橘子，好的橘子，空的，分为用2，1, 0 表示，然后一个橘子坏掉了，在接下来的1s里，周围4个方向的橘子都会坏掉。问，最后最少多长时间全部坏掉。

解析：其实就是BFS的应用，首先遍历一遍棋盘，如果存在一个好的橘子4个方向都都是空，那么直接返回-1，因为它不会被坏掉。然后就是BFS了，每次取队列里所有为2的节点，然后进行扩展，如果某一次，有橘子没有被感染，但是队列里又没有坏的橘子了，说明存在大于1个的联通分量，那么返回-1. 否则最后的结果就是BFS的层数。

代码：

class Solution
{
public:
	bool judge(int x, int y, int rows, int cols)
	{
		if (x<0 || y<0 || x>rows || y>cols) return false;
		return true;
	}

	struct Node
	{
		int x, y;
	};

	int orangesRotting(vector>& grid)
	{
		int dx[4] = { -1, 1, 0, 0 };
		int dy[4] = { 0, 0, -1, 1 };
		int rows = grid.size();
		int cols = grid[0].size();

		bool flag;

		int o2 = 0; // 坏橘子的个数
		int cnt = 0;  // 橘子数量
		int blank = 0;
		queue Q;
		Node cur;
		for (int i = 0; i < rows; i++)
		{
			for (int j = 0; j