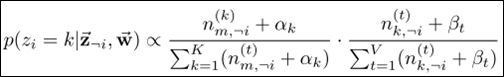LDA模型算法简介:
算法 的输入是一个文档的集合D={d1, d2, d3, ... , dn},同时还需要聚类的类别数量m;然后会算法会将每一篇文档 di 在 所有Topic上的一个概率值p;这样每篇文档都会得到一个概率的集合di=(dp1,dp2,..., dpm);同样的文档中的所有词也会求出 它对应每个Topic的概率,wi = (wp1,wp2,wp3,...,wpm);这样就得到了两个矩阵,一个文档到Topic,一个词到Topic。
这样LDA算法,就将文档和词,投射到了一组Topic上,试图通过Topic找出文档与词间,文档与文档间,词于词之间潜在的关系;由于LDA属于无监督算法,每个Topic并不会要求指定条件,但聚类后,通过统计出各个Topic上词的概率分布,那些在该Topic上概率高的词,能非常好的描述该Topic的意义。
LDA模型构建原理:
在讲LDA模型之前,会先介绍下 Unigram Model (词袋模型)、Bayes Unigram Model(贝叶斯词袋模型),以及PLSA 概率潜在语义分析,之所以先介绍这些模型,首先它们是LDA模型的基础,LDA是将它们组合和演变的结果;其次这些模型比简单,了解起来会容易些。
1、Unigram Model(词袋模型)
LDA既然是聚类算法,而聚类算法大多数时候,都在寻找两个东西的相似度。
最开始,大家想要判断两篇文档是否相似,最简单直接的方法就是看文档里出现的词是否一样,其个数是否相近。于Unigram Model(词袋模型)就是实现这样的思路设计的。所以为了得到文档集合中,所有文档的共性的规律,词袋模型,假设:一篇文档生成的过程就是 独立的抛一个具有M面的骰子(M是所有词的个数),N次(N是该文档里词的个数),这样文档的生成,刚好可以看作是个多项式分布:
文档集合中,每个词出现的概率就是要求的参数,通过EM算法可以确定下来,这样就得到了模型。
2、Bayes Unigram Model(贝叶斯词袋模型)
在词袋模型中,我们简单的认为文档里每个词出现的概率是个定数(即骰子的每个面的概率),但Bayes学派不这么认为,他们认为这些概率应该是一个随机过程产生的,于是生成一篇文档的过程可以描述为:先随机抽取一个M面的骰子, 再用这个骰子独立抛N次。那么这个模型的分布如下:
其中后边部分![]() ,是多项式分布,我们已经知道,为了方便计算我们假设
,是多项式分布,我们已经知道,为了方便计算我们假设![]() 为Dirichlet分布,它是多项式分布的共轴分布
为Dirichlet分布,它是多项式分布的共轴分布
简单介绍下 Dirichlet 分布:比如 抛了100次骰子,得到6个面的一个概率,记为一个实验,重复这个实验100次,那么这100次的实验中,这6个面的概率的概率分布,就是Dirichlet分布,它是分布之上的分布。
例如:1点(骰子六个面之一) 在这100次实验(每个实验抛100次) 是 0.15的概率为 0.12,实际我们这么想,100次实验中,有12次,1点在一个实验内出现了15次,可以看作是总共抛10000次,1点出现15×12=180次。这10000次实验,视为一个大的多项式分布,于是可以得出他们有相同的概率分布公式,这就是前面所提到的共轴分布,且有如下性质:
先验的Dirichlet分布+多项式分布 = 后验的Dirichlet分布
上述的例子中,你会发现,它与我们的Bayes Unigram Model(贝叶斯词袋模型)已经很相似了。一个实验里的100次抛骰子,可以看作是先验的Dirichlet分布,也就是模型中确定骰子各个面概率的那个随机过程,而重复这个这个实验100次,可以看作是后面的根据这个骰子确定文档的一个过程。
Dirichlet分布还有一个重要的性质,它的最大似然估计可以通过如下公式,证明过程有些复杂,暂不推导了:
3、PLSA潜在语义分析
在文本聚类的时候,常常会遇到这样一种问题:例如在NBA的相关新闻中提到“石佛”,和提到“邓肯”它们应该是指的同一个人,确实两个不同的词;而另一篇关于教育的新闻里也提到了“邓肯”,但此“邓肯”非彼“邓肯”,它可能指的是美国教育部部长“阿恩·邓肯”;而这两篇NBA新闻和一篇教育新闻,很可能就被错误的聚类了。
于是,可以发现词在不同的语义环境下,同一个词可能表达不同意思,而同一个意思可能产生不同的词。PLSA潜在语义分析,就是为了解决这样的问题。它在文档和词之间加了一层主题(Topic),先让文档和主题产生关联,再在主题中寻找词的概率分布。
PLSA模型将文档的生成这样设计:第一步,我们抛一个有H面的骰子,每个面代表一个主题,各个面概率不一,得到一个主题;第二步,这个主题又对应了一个有T个面的骰子,每个面代表一个词,抛这骰子N次,得到一篇文章。其实我觉得这个模型可以看作是两个词袋模型的组合,第一个做一次,确定主题,第二个重复独立做N词,确定文章。下面是一个直观图(借用LDA数学八卦的图了):
这样概率分布公式如下:
LDA主题聚类模型
这时Bayes学派的朋友们又出现,历史是如此的相似,他们又对PLSA下手了,认为PLSA里面的两种骰子(产生主题的骰子和主题对应词的骰子),各个面的概率都不应该是确定,应该由一个随机过程来得出。于是让PLSA的两个词袋模型,变成两个Bayes词袋模型,就是LDA了
前面已经介绍了,Bayes词袋模型的概率分布是一个Dirichlet 同轴分布,LDA 的整个物理过程实际就是两个Dirichlet 同轴分布,而 LDA 模型的参数估计也就出来了,通过那个重要的性质,如下:
LDA 算法设计 与Gibbs Sampling
算法步骤:
1. 对文档集合中的每篇文档d,做分词,并过滤掉无意义词,得到语料集合W = {w1, w2, …, wx}。
2. 对这些词做统计,得到 p(wi|d)。
3. 为语料集合W中的每个 wi ,随机指定一个主题 t,作为初始主题。
4. 通过 Gibbs Sampling 公式, 重新采样 每个 w 的所属 主题t, 并在语料中更新 直到Gibbs Sampling 收敛。
收敛以后得到 主题-词 的概率矩阵,这个就是LDA矩阵,而 文档-主题的的概率矩阵也是能得到的,统计后,就能能得到文档-主题的概率分布。
Gibbs Sampling 公式:
Gibbs Sampling 公式,可以用于计算 某x维度的空间中,两个平行点之间转移的概率。 比如在 二维空间(x, y平面),点a(x1,y1) 转移到 b(x1,y2)的概率记为P,P(a ->b) = p(y2|x1 )
于是上述中第4步,可以视为我们将一个词对应的 文档和Topic的概率 看作是一个点在二维平面里的两个维度,词在不同的文档和不同的主题里,通过Gibbs Sampling公式,不断的转移(即重新采样),直至收敛。 下面是Gibbs Sampling公式收敛的一个图,可以给大家一个直观印象(来自LDA数学八卦)。
LDA(Latent Dirichlet Allocation)学习笔记
示例
LDA要干的事情简单来说就是为一堆文档进行聚类(所以是非监督学习),一种topic就是一类,要聚成的topic数目是事先指定的。聚类的结果是一个概率,而不是布尔型的100%属于某个类。国外有个博客[1]上有一个清晰的例子,直接引用:
Suppose you have the following set of sentences:
- I like to eat broccoli and bananas.
- I ate a banana and spinach smoothie for breakfast.
- Chinchillas and kittens are cute.
- My sister adopted a kitten yesterday.
- Look at this cute hamster munching on a piece of broccoli.
What is latent Dirichlet allocation? It’s a way of automatically discovering topics that these sentences contain. For example, given these sentences and asked for 2 topics, LDA might produce something like
- Sentences 1 and 2: 100% Topic A
- Sentences 3 and 4: 100% Topic B
- Sentence 5: 60% Topic A, 40% Topic B
- Topic A: 30% broccoli, 15% bananas, 10% breakfast, 10% munching, … (at which point, you could interpret topic A to be about food)
- Topic B: 20% chinchillas, 20% kittens, 20% cute, 15% hamster, … (at which point, you could interpret topic B to be about cute animals)
上面关于sentence 5的结果,可以看出来是一个明显的概率类型的聚类结果(sentence 1和2正好都是100%的确定性结果)。
再看例子里的结果,除了为每句话得出了一个概率的聚类结果,而且对每个Topic,都有代表性的词以及一个比例。以Topic A为例,就是说所有对应到Topic A的词里面,有30%的词是broccoli。在LDA算法中,会把每一个文档中的每一个词对应到一个Topic,所以能算出上面这个比例。这些词为描述这个Topic起了一个很好的指导意义,我想这就是LDA区别于传统文本聚类的优势吧。
LDA整体流程
先定义一些字母的含义:
- 文档集合D,topic集合T
- D中每个文档d看作一个单词序列< w1,w2,...,wn >,wi表示第i个单词,设d有n个单词。(LDA里面称之为word bag,实际上每个单词的出现位置对LDA算法无影响)
- D中涉及的所有不同单词组成一个大集合VOCABULARY(简称VOC)
LDA以文档集合D作为输入(会有切词,去停用词,取词干等常见的预处理,略去不表),希望训练出的两个结果向量(设聚成k个Topic,VOC中共包含m个词):
- 对每个D中的文档d,对应到不同topic的概率θd < pt1,..., ptk >,其中,pti表示d对应T中第i个topic的概率。计算方法是直观的,pti=nti/n,其中nti表示d中对应第i个topic的词的数目,n是d中所有词的总数。
- 对每个T中的topic t,生成不同单词的概率φt < pw1,..., pwm >,其中,pwi表示t生成VOC中第i个单词的概率。计算方法同样很直观,pwi=Nwi/N,其中Nwi表示对应到topic t的VOC中第i个单词的数目,N表示所有对应到topic t的单词总数。
LDA的核心公式如下:
p(w|d) = p(w|t)*p(t|d)
直观的看这个公式,就是以Topic作为中间层,可以通过当前的θd和φt给出了文档d中出现单词w的概率。其中p(t|d)利用θd计算得到,p(w|t)利用φt计算得到。
实际上,利用当前的θd和φt,我们可以为一个文档中的一个单词计算它对应任意一个Topic时的p(w|d),然后根据这些结果来更新这个词应该对应的topic。然后,如果这个更新改变了这个单词所对应的Topic,就会反过来影响θd和φt。
LDA算法开始时,先随机地给θd和φt赋值(对所有的d和t)。然后上述过程不断重复,最终收敛到的结果就是LDA的输出。
文章转自:https://blog.csdn.net/zhazhiqiang/article/details/21186353