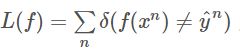机器学习笔记(二)-感知机
原创不易,转载前请注明博主的链接地址:Blessy_Zhu https://blog.csdn.net/weixin_42555080
本次代码的环境:
运行平台: Windows
Python版本: Python3.x
IDE: PyCharm
一、 前言
在文章机器学习笔记-线性回归中的前言部分已经介绍了,当打破线性回归的某一特性,就会形成新的模型算法,这篇文章介绍的感知机就是尝试打破了线性中的全局非线性这一性质——它是将线性回归得出的值,作为激励函数的输入,进而进行二分类的一种算法。在介绍感知机之前呢!还是先认识一下分类问题中的二分类问题是什么:
二分类:二次分类器是在机器学习中,使用二次曲面来将物件或事件分成两个或以上的分类。 它是线性分类器的一般化版本。
其中二分类又分为软分类和硬分类问题:
- 软分类:使用的是概率模型,输出不同类对应的概率,最后的分类结果取概率最大的类,如多SVM组合分类;
- 硬分类:使用的是非概率模型,分类结果就是决策函数的决策结果:比如今天介绍的感知机模型就是这样的硬分类模型。
如下图所示可以反映一些问题,可以看出硬分类最终的结果就是分出来两类0类或者1类(也可以说是正类和负类),而软分类得到的就是不同类对应的概率值:

接下来开始介绍感知机模型。
二、 感知机模型Perceptron
2.1 背景介绍
根据刚才介绍可知,感知机模型属于线性分类中的一种
在机器学习领域,分类的目标是指将具有相似特征的对象聚集。而一个线性分类器则透过特征的线性组合来做出分类决定,以达到此种目的。对象的特征通常被描述为特征值,而在向量中则描述为特征向量。
分类问题的求解过程同样可以分为三个步骤:
1、确定一个模型f(x),输入样本数据x,输出其类别;
2、定义损失函数L(f),一个最简单的想法是计数分类错误的次数,
3、找出使损失函数最小的那个最优函数。
再看一下二分类的问题,实际上也是将线性回归得到的结果作为输入值给激活函数,对于感知机,激活函数会直接给出分类结果(+1和-1),这里将激活函数的反函数叫做链接函数,这里面线性回归、激活函数和链接函数的关系,如下图所示:

说到感知机,它是个相当简单的模型,但它既可以发展成支持向量机(通过简单地修改一下损失函数)、又可以发展成神经网络(通过简单地堆叠),所以它也拥有一定的地位。实际上深度学习最原始的神经网络就是多层感知机。这样一来认识到了感知机的重要性,接下来就开始学习啦!!!!
2.2 感知机内容介绍
感知机的核心思想就是:错误驱动
什么是错误驱动呢?这里分别用自然语言和定量操作来介绍:
- 自然语言描述:
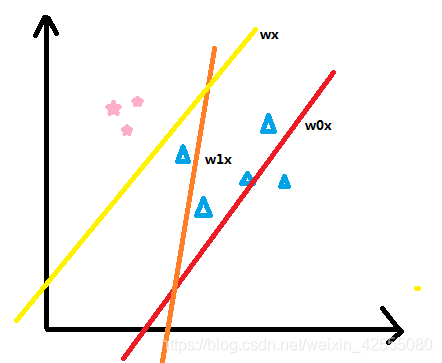
如上图所示,所谓的错误驱动:如图共有8个样本点,3个五角星,5个三角,第一次任意选择一条直线,将样本分为两类,如图中的红色线w0x,这时候发现有4个三角被分类错误;然后在选择一条直线w1x,如图中的橙色线,发现还是有1个三角被错误分到了五角星那一类了;接下来继续一步步调整,直到调整到被分错的值无法再小为止。通过上图可以看到,最终分到的结果就是如黄色线wx所示,正好被分为五角星一类三角形一类。达到目的。
- 定量描述
过程如下图所示:
如上图,这里面定义了数据集合D:{被错误分类的样本}
具体内容如上图所示,如果又不理解的,可以进一步交流。
三、 验证
首先看一下数据长什么样子,其实这些数据可以通过radom函数随机生成:
接下俩开始正式通过感知机进行数据的分类:
3.1 数据导入
如上图展示的数据,数据集包含了100个样本,正负样本各50,特征维度为2:
import pandas as pd
data = pd.read_csv('C:/Users/Administrator/Desktop/12.csv', header=None)
# 样本输入,维度(100,2)
X = data.iloc[:,:2].values#选取数据和纬度iloc[x:y,n:m],第一个是选取的数据,第二个参数是选取的纬度
# 样本输出,维度(100,)
Y = data.iloc[:,2].values
#print(X)
#print(Y)
3.2 数据分类与可视化
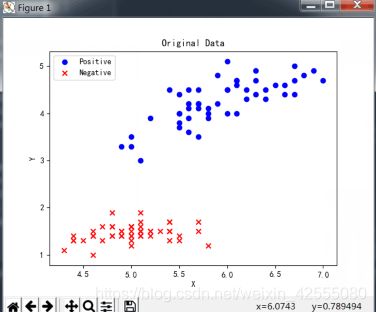
将原始数据在二维图上进行展示:
import matplotlib.pyplot as plt
plt.scatter(X[:50, 0], X[:50, 1], color='blue', marker='o', label='Positive')
plt.scatter(X[50:, 0], X[50:, 1], color='red', marker='x', label='Negative')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend(loc = 'upper left')
plt.title('Original Data')
plt.show()
结果如下:
3.3 特征标准化处理
首先分别对两个特征进行标准化处理,即:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_csv('C:/Users/Administrator/Desktop/12.csv', header=None)
# 样本输入,维度(100,2)
X = data.iloc[:,:2].values#选取数据和纬度iloc[x:y,n:m],第一个是选取的数据,第二个参数是选取的纬度
# 样本输出,维度(100,)
Y = data.iloc[:,2].values
# 均值
u = np.mean(X, axis=0)
# 方差
v = np.std(X, axis=0)
X = (X - u) / v
print(X)
# 作图
plt.scatter(X[:50, 0], X[:50, 1], color='blue', marker='o', label='Positive')
plt.scatter(X[50:, 0], X[50:, 1], color='red', marker='x', label='Negative')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend(loc = 'upper left')
plt.title('Normalization data')
plt.show()
结果:
3.4 直线初始化
随机生成一条直线,用于划分数据。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = pd.read_csv('C:/Users/Administrator/Desktop/12.csv', header=None)
# 样本输入,维度(100,2)
X = data.iloc[:,:2].values#选取数据和纬度iloc[x:y,n:m],第一个是选取的数据,第二个参数是选取的纬度
# 样本输出,维度(100,)
Y = data.iloc[:,2].values
# 均值
u = np.mean(X, axis=0)
# 方差
v = np.std(X, axis=0)
X = (X - u) / v
#print(X)
# X加上偏置项
X = np.hstack((np.ones((X.shape[0],1)), X))
# 权重初始化
w = np.random.randn(3,1)#随机生成一个1行3列的数组
#print(w)
# 直线第一个坐标(x1,y1)
x1 = -2
y1 = -1 / w[2] * (w[0] * 1 + w[1] * x1)
# 直线第二个坐标(x2,y2)
x2 = 2
y2 = -1 / w[2] * (w[0] * 1 + w[1] * x2)
# 作图
plt.scatter(X[:50, 1], X[:50, 2], color='blue', marker='o', label='Positive')
plt.scatter(X[50:, 1], X[50:, 2], color='red', marker='x', label='Negative')
plt.plot([x1,x2], [y1,y2],'r')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend(loc = 'upper left')
plt.show()
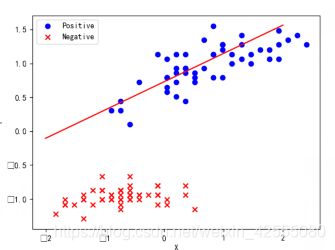
结果:
3.5 更新权重
上面直线的误分率很高,接下来就是计算scores,更新权重:接下来,计算scores,得分函数与阈值0做比较,大于零则y^ =1,小于零则y^=−1:
s = np.dot(X, w)
y_pred = np.ones_like(y) # 预测输出初始化
loc_n = np.where(s < 0)[0] # 大于零索引下标
y_pred[loc_n] = -1
接着,从分类错误的样本中选择一个,使用PLA更新权重系数w。
# 第一个分类错误的点
t = np.where(y != y_pred)[0][0]
# 更新权重w
w += y[t] * X[t, :].reshape((3,1))
3.6 迭代更新训练,找到最终的权值,并绘制直线
更新权重w是个迭代过程,只要存在分类错误的样本,就不断进行更新,直至误分率最小的那条直线为止,然后绘制直线,完整代码如下:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#读取数据
data = pd.read_csv('C:/Users/Administrator/Desktop/12.csv', header=None)
# 样本输入,维度(100,2)
X = data.iloc[:,:2].values#选取数据和纬度iloc[x:y,n:m],第一个是选取的数据,第二个参数是选取的纬度
# 样本输出,维度(100,)
Y = data.iloc[:,2].values
#数据标准化
# 均值
u = np.mean(X, axis=0)
# 方差
v = np.std(X, axis=0)
X = (X - u) / v
#print(X)
# X加上偏置项
X = np.hstack((np.ones((X.shape[0],1)), X))
# 权重初始化
w = np.random.randn(3,1)
#迭代更新训练
for i in range(100):
s = np.dot(X, w)
y_pred = np.ones_like(Y)
loc_n = np.where(s < 0)[0]
y_pred[loc_n] = -1
num_fault = len(np.where(Y != y_pred)[0])
print('第%2d次更新,分类错误的点个数:%2d' % (i, num_fault))
if num_fault == 0:
break
else:
t = np.where(Y != y_pred)[0][0]
w += Y[t] * X[t, :].reshape((3,1))
#绘制分类的直线
# 直线第一个坐标(x1,y1)
x1 = -2
y1 = -1 / w[2] * (w[0] * 1 + w[1] * x1)
# 直线第二个坐标(x2,y2)
x2 = 2
y2 = -1 / w[2] * (w[0] * 1 + w[1] * x2)
# 作图
plt.scatter(X[:50, 1], X[:50, 2], color='blue', marker='o', label='Positive')
plt.scatter(X[50:, 1], X[50:, 2], color='red', marker='x', label='Negative')
plt.plot([x1,x2], [y1,y2],'r')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend(loc = 'upper left')
plt.show()
运行了6次的结果如下图所示:
四、 总结
本篇内容主要介绍了感知机,并对感知机模型进行验证。这篇文章就到这里了,欢迎大佬们多批评指正,也欢迎大家积极评论多多交流。
参考文章:
1 机器学习系列(七)——分类问题(classification)
2 机器学习(二)— 分类算法详解
3 机器学习——15分钟透彻理解感知机
4 机器学习——感知机python可视化实现
5 一看就懂的感知机算法PLA
6 机器学习算法–Perceptron(感知机)算法
7 机器学习笔记——感知机