异常值检测——孤立森林(Isolation Forest)
孤立森林(Isolation Forest)简称iForest,此算法对内存要求很低,且处理速度很快,其时间复杂度也是线性的。可以很好的处理高维数据和大数据,并且也可以作为在线异常检测。
算法简介
算法起源于2008年的一篇论文《Isolation Forest》【第八届IEEE数据挖掘国际会议】,这论文由澳大利亚莫纳什大学的两位教授Fei Tony Liu, Kai Ming Ting和南京大学的周志华教授共同完成,而这三人在2011年又发表了《Isolation-based Anomaly Detection》,这两篇论文算是确定了这个算法的基础,之后又于2012年提出了改进版本。
在孤立森林(iForest)中,异常被定义为“容易被孤立的离群点 (more likely to be separated)”,可以将其理解为分布稀疏且离密度高的群体较远的点。 在特征空间里,分布稀疏的区域表示事件发生在该区域的概率很低,因而可以认为落在这些区域里的数据是异常的。
孤立森林是一种适用于连续数据(Continuous numerical data)的无监督异常检测方法,即不需要有标记的样本来训练,但特征需要是连续的,且该算法对高纬数据有较好的鲁棒性。
论文地址:
http://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/icdm08b.pdf
http://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/tkdd11.pdf
算法原理
iForest森林与随机森林由大量决策树组成一样,iForest森林也由大量的树组成。iForest中的树叫isolation tree,简称iTree。iTree树和决策树不太一样,其构建过程也比决策树简单,因为其中就是一个完全随机的过程。
假设数据集有N条数据,构建一颗iTree时,从N条数据中均匀抽样(一般是无放回抽样)出ψ个样本出来,作为这颗树的训练样本。
在样本中,随机选一个特征,并在这个特征的所有值范围内(最小值与最大值之间)随机选一个值,对样本进行二叉划分,将样本中小于该值的划分到节点的左边,大于等于该值的划分到节点的右边。
这样得到了一个分裂条件和左、右两边的数据集,然后分别在左右两边的数据集上重复上面的过程,直接达到终止条件。终止条件有两个,一个是数据本身不可再分(只包括一个样本,或者全部样本相同),另外一个是树的高度达到log2(ψ)。不同于决策树,iTree在算法里面已经限制了树的高度。当然不限制也可以,只是算法为了效率考虑,只需要达到log2(ψ)深度即可。
把所有的iTree树构建好了,就可以对测数据进行预测了。预测的过程就是把测试数据在iTree树上沿对应的条件分支往下走,直到达到叶子节点,并记录这过程中经过的路径长度h(x),即从根节点,穿过中间的节点,最后到达叶子节点,所走过的边的数量(path length)。在这种随机分割的策略下,异常点通常具有较短的路径。
最后,将h(x)带入,计算每条待测数据的异常分数(Anomaly Score),其计算公式为:
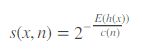
树的平均路径长度为c(n):
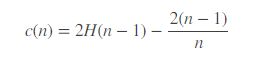
其中H(i)为调和数,该值可以被估计为ln(i)+0.5772156649。c(n)为给定样本数n时,路径长度的平均值,用来标准化样本x的路径长度h(x)。
其中,E(h(x))为样本x在一批孤立树中的路径长度的期望。下图给出了s和E(h(x))的关系。

由上图可以得到一些结论:
- 当E(h(x))→c(n)时,s→0.5,即样本x的路径平均长度与树的平均路径长度相近时,则不能区分是不是异常。
- 当E(h(x))→0时,s→1,即x的异常分数接近1时,被判定为异常。
- 当E(h(x))→n−1时,s→0,被判定为正常。
简单解释为:使用异常分数时,具有以下性质:
1、如果分数越接近1,其是异常点的可能性越高;
2、如果分数都比0.5要小,那么基本可以确定为正常数据;
3、如果所有分数都在0.5附近,那么数据不包含明显的异常样本。
上面的步骤,可以总结为两步:
1、训练:从训练集中进行采样,并构建iTree树;
2、测试:对iForest森林中的每颗iTree树进行测试,记录path length,然后根据异常分数计算公式,计算每条测试数据的anomaly score。
算法特点
在论文中,也比较了其它的常用异常挖掘的算法。比如常用的统计方法,基于分类的方法,和基于聚类的方法,这些传统算法通常是对正常的数据构建一个模型,然后把不符合这个模型的数据,认为是异常数据。而且,这些模型通常为正常数据作优化,而不是为异常数据作优化。而iForest可以显示地找出异常数据,而不用对正常的数据构建模型。
已经存在的那些异常检测的方法大部分都期望有更多的数据,但是在孤立森林中,小数据集往往能取得更好的效果。样本数较多会降低孤立森林孤立异常点的能力,因为正常样本会干扰隔离的过程,降低隔离异常的能力。子采样就是在这种情况下被提出的。
以下为异常数据的两个特征(少且不同: few and different):
1、异常数据只占很少量;
2、异常数据特征值和正常数据差别很大。
异常数据的这两个特征,确定了算法的理论基础。因此,构建二叉树型结构的时候,异常数据离根更近,而正常数据离根更远,更深。算法为了效率考虑,也限定了树的深度:ceil(log2(n)),这个值近似于树的平均深度,因为只需要关心那些低于平均高度的数据点,而不需要树进行完全生成。
算法只需要两个参数:树的多少与采样的多少。实验发现,在100颗树的时候,路径的长度就已经覆盖得比较好了,因此选100颗也就够了。采样,是为了更好的将正常数据和异常数据分离开来。有别于其它模型,采样数据越多,反面会降低iForest识别异常数据的能力。因为,通常使用256个样本,这也是scikit-learn实现时默认使用的采样数。
由于算法只需要采样数据256条样本,并且对树的深度也有限制,因此,算法对内存要求很低,且处理速度很快,其时间复杂度也是线性的。
不像其它算法,需要计算距离或者密度来寻找异常数据,iForest算法可以很好的处理高维数据和大数据,并且也可以作为在线预测。假设采样为256条,结点最大为511个,假设一个节点占b字节,共使用t颗树,那么需要的内存只有511tb字节,基本上只需要几M到几十M的内存就够了。数据还显示,预测287,748条数据只花了7.6秒。
另外,iForest既能发现群异常数据,也能发现散点异常数据。同时也能处理训练数据中不包含异常数据的情况。
sklearn示例
IsolationForest在scikit-learn的0.18中才有实现,scikit-learn目前的stable版本为0.17,而0.18是dev版本。需要直接去github中clone。
源码和文档地址:
https://github.com/scikit-learn/scikitlearn/blob/master/sklearn/ensemble/iforest.py
http://scikit-learn.org/dev/modules/generated/sklearn.ensemble.IsolationForest.html
下载源码与安装:
git clone https://github.com/scikit-learn/scikit-learn.git
cd scikit-learn
python setup.py install
算法基本上不需要配置参数就可以直接使用,通常就以下几个(参数明显比随机森林简单):
n_estimators: 默认为100,配置iTree树的多少
max_samples: 默认为265,配置采样大小
max_features: 默认为全部特征,对高维数据,可以只选取部分特征
Tree height: 8层
示例:
import pandas as pd
from sklearn.ensemble import IsolationForest
ilf = IsolationForest(n_estimators=100,
n_jobs=-1, # 使用全部cpu
verbose=2,
)
data = pd.read_csv('data.csv', index_col="id")
data = data.fillna(0)
# 选取特征,不使用标签(类型)
X_cols = ["age", "salary", "sex"]
print data.shape
# 训练
ilf.fit(data[X_cols])
shape = data.shape[0]
batch = 10**6
all_pred = []
for i in range(shape/batch+1):
start = i * batch
end = (i+1) * batch
test = data[X_cols][start:end]
# 预测
pred = ilf.predict(test)
all_pred.extend(pred)
data['pred'] = all_pred
data.to_csv('outliers.csv', columns=["pred",], header=False)
算法的训练过程需要的内存很少,但如果数据量太大,在预测的时候,可能会把内存挤爆,上面代码中的for循环便是分块对数据进行预测,最后再组合起来。
参考链接I
参考链接II
参考链接III