20200529机器学习在物理学中的应用

机器学习在物理学中的应用

0. 前言

本文是我为了完成物理学中的数值方法||课程作业而写下的，作业的要求是“谈一下机器学习方法在你的专业领域（凝聚态物理学）可能的应用”。我认为为了完成该作业，有必要具体学习一下什么是机器学习，因此观看学习了吴恩达老师的机器学习课程^1​。本文前半部分是机器学习课程的课程笔记，对机器学习是什么以及机器学习如何运作作了一个简要的介绍。后半部分简要介绍一篇物理学中应用机器学习的文献。
​

1. 机器学习简介${}^1$

机器学习可以定义为（Tom Mitchell，1998）：一个电脑程序在面对某一个目标T（Task），通过经验E（Experience）学习，提升达成目标的能力P（Performance Measure）。在1950年代，Arthur Samuel编写了一个跳棋游戏程序，通过让程序自己对弈上万次，观察何种布局更容易赢，何种布局更容易输（经验E），提升了程序玩跳棋的能力（能力P），使得该跳棋程序学会了玩跳棋（目标T），并最终打败了编写程序的作者本人。机器学习的优势在于可以处理大量数据，从大量数据中寻找规律，并进行预测。
​
机器学习具体可以分为两类：监督学习（Supervised learning）与无监督学习（Unsupervised learning）。监督学习与无监督学习的区别在于是否有训练样本提供给程序进行学习。监督学习通过学习训练样本得到一个模型，然后用这个模型进行预测，典型的例子有线性回归（Linear Regression）和分类（Classification）；无监督学习没有训练过程，给定一些样本数据，让程序利用算法直接对数据进行分析，典型的例子就是分类（Classification）。
​

2. 监督学习

在此具体考虑监督学习算法，即给定训练样本，通过学习、拟合，寻找最优拟合函数形式。设训练样本个数为$m$，样本输入变量为$x$，样本输出变量为$y$，$(x^m,y^m)$代表一个样本数据点。机器学习需要寻找的是输入变量$x$与输出变量$y$的函数关系$y=h_{\theta }(x)$，其中$h$称为假设函数（Hypothesis function），$\theta$称为参数（在神经网络中$\theta$称为权重（Weight））。机器学习的过程就是利用训练样本的数据点不断调整、优化参数$\theta$使得假设函数$h_{\theta }(x^m)-y^m\approx 0$，此时定义代价函数（Cost function）（在神经网络中称为Loss function）$J(\theta )=\frac{1}{2m}{\sum }_m(h_{\theta }(x^m)-y^m{)}^2$，因此最优化的过程其实就是寻找参数$\theta$使代价函数$J(\theta )$达到最小值，完全拟合时$J(\theta )=0$。
​
在多数情况下输入变量$x$可以是多维度的即$x_1,x_2...,x_n$，$n$代表输入变量不同的特征，$(x_1^m,x_2^m,...,x_n^m,y^m)$代表一个样本数据点。此时假设函数就是以$x_1,x_2...,x_n$为变量的多元函数$y=h_{\theta }(x_1,x_2...,x_n)$，代价函数为$J(\theta )=\frac{1}{2m}{\sum }_m(h_{\theta }(x_1^m,x_2^m,...x_n^m)-y^m{)}^2$。
​
机器学习在该场景下为，通过训练样本数据点$(x_1^m,x_2^m,...,x_n^m,y^m)$（经验E）进行拟合学习，提升拟合程度$J(\theta )\to 0$（能力P），找到训练样本中的函数曲线$y=h_{\theta }(x_1,x_2...,x_n)$（目标T）。利用机器学习得到的函数曲线，可以对未来的数据进行预测。因此机器学习本质上而言，是一个大型的函数拟合器。
​
对于不同的样本数据点，数据分布需要使用不同形式的假设函数$y=h_{\theta }(x)$。
​
最简单的假设函数可以是线性的$h_{\theta }={\sum }_n{\theta }_n\ast x_n$，这样的机器学习过程称为线性回归（Linear Regression）。寻找线性回归代价函数$J(\theta )$的极值有两种方法，一种为正规方程（Normal Equation）方法，一种为梯度下降算法（Gradient Descent）。正规方程方法是计算偏导数$\frac{\partial J({\theta }_n)}{{\theta }_n}$，直接找到代价函数极值位置，该方法需要的计算量是$O(n^3)$（需要计算$n\ast n$维矩阵的逆），$n$为样本特征数量。当样本特征数量很大时，如样本特征为不同的像素点$n\approx 10^6$，正规方程方法几乎是不可用的（$O(10^{18})$）。梯度下降算法通过计算代价函数$J(\theta )$某一点的的梯度，寻找使代价函数数值下降的方向，并进行迭代，最终收敛至代价函数最小值的位置。梯度下架算法每一次下降的计算量为$O(n)$，因此适合处理样本特征数量巨大（$n>>1$）的情况。
​
假设函数可以是非线性的，例如假设函数可以包含输入变量$x_n$的二次项，此时假设函数中会包含$x_1^2,x_1{x}_2,x_2^2...$等自变量，自变量的个数约为$O(n^2)$。假设函数也可以包含输入变量$x_n$的三次项，此时假设函数中会包含$x_1^3,x_1{x}_2{x}_3,x_2^3...$等自变量，自变量的个数约为$O(n^3)$。对于这样的多项式假设函数，任然可以通过梯度下降算法寻找代价函数的最小值。但由于此时代价函数可能存在局域最小值，因此可以使用随机梯度下降算法寻找代价函数的最小值。
​
对于前三种情况，假设函数都是先验地知道假设函数的函数形式，通过具体方法对样本数据进行拟合。如果无法先验地知道假设函数的函数形式，需要引入输入变量的高阶多项式，即假设函数的泰勒展开，此时拟合函数需要的参数$\theta$的数量会以$O(n^{m+1})$迅速上升（$m$为假设函数自变量的最高阶）。利用回归的方法拟合复杂的非线性假设函数需要的计算量是完全超出现有计算能力的，因此回归算法不适用于复杂的非线性拟合。
​

3. 神经网络

3.1 神经网络模型

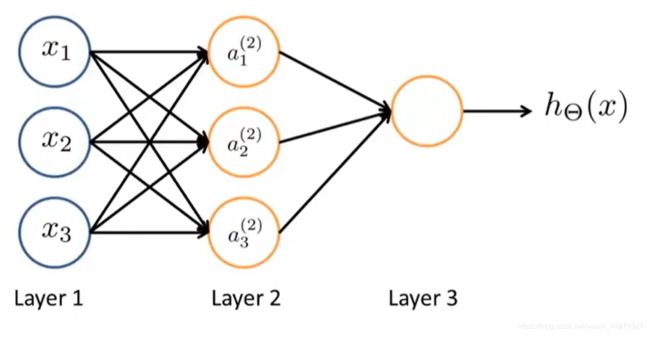
神经网络（Neural Networks）算法在学习复杂的非线性假设函数上被证明是十分有效的。神经网络算法通常都有如下图所示的结构。

神经网络分为多个层，第一层称为输入层，最后一层称为输出层，第一层与最后一层中间的所有层都成为隐藏层。输入层输入的信息是机器学习的输入变量$x$，输出层输出的信息是假设函数$h_{\theta }(x)$的输出值。机器学习通过样本数据，最优化代价函数$J(\theta )$，使得输出的假设函数$h_{\theta }(x)$与样本输出变量$y$拟合达到最好。
​
神经网络与回归算法本质是相同的，寻找对样本数据拟合最好的函数，两者的区别在于神经网络的隐藏层。神经网络隐藏层的存在使得这个算法可以很有效地进行复杂非线性假设函数的拟合。神经网络中层与层的连接由权重$\theta$决定，例如图中$a_1^{(2)}=a_1^{(2)}({\theta }_{11}^{(1)}{x}_1+{\theta }_{21}^{(1)}{x}_2+{\theta }_{31}^{(1)}{x}_3)=a_1^{(2)}({{\theta }_1}^T\cdot x)$，在机器学习的过程中，通过调节层间连接的权重$\theta$使得代价函数$J(\theta )$最优，进而得到假设函数$h_{\theta }(x)$。
​
通过线性代数的知识知道，如果在隐藏层不做任何函数处理仅线性传递至下一层的话，即$a_1^{(2)}({\theta }^T\cdot x)={\theta }_0+{\theta }^T\cdot x$，当每一层都是线性传递，最终得到的代价函数任然是输入变量的线性组合，因此该情况下神经网络与线性回归算法没有区别。因此需要在隐藏层的每一个节点做一定的运算，才可以使得假设函数$h_{\theta }(x)$是非线性的（也是我们想要的）。在每一个隐藏层的节点都会做一个非线性运算，这个运算通常是$sigmoid$函数，即，$f(x)=\frac{1}{1+e^{-x}}$。在隐藏层的节点中表示为，$a_1^{(2)}({{\theta }_1}^T\cdot x)=\frac{1}{1+e^{-{{\theta }_1}^T\cdot x}}$。$sigmoid$函数与费米狄拉克分布函数十分相似，输出的值在$(0,1)$区间，当输入值是很大的负数输出为0，当输入的值是很大的正数输出为一。因此该函数本质上将输入的值进行了分类。
​

3.2 神经网络拟合任意函数${}^2$

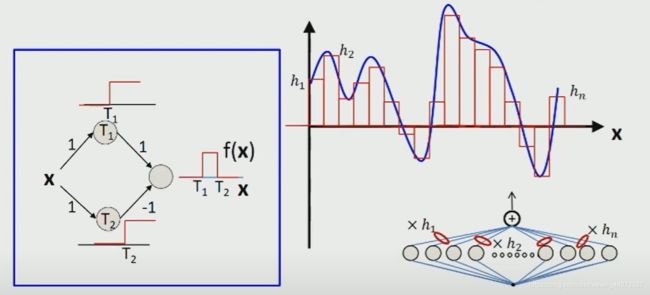
考虑如下图左侧图片所示的神经网络，图中的数字代表权重$\theta$，$+$代表与函数。

通过如图所示的神经网络，可以得到关于输入变量$x$的脉冲函数。利用这样最简单的神经元得到的脉冲函数，可以对任意非线性函数完成任意精度的拟合，如上图右上角所示。利用多个神经元和多个隐藏层便可以实现对复杂非线性函数的拟合。
​

4. 利用机器学习分辨物质的相${}^3$

物理学中的凝聚态体系是十分复杂的，其复杂性主要体现在电子、原子核等基本单位的多体相互作用。凝聚态体系研究的对象通常具有大量粒子（~10²³量级），因此凝聚态物理研究的波函数存在的希尔伯特空间是十分巨大的。对于模拟研究如此巨大的体系，可以使用蒙特卡洛模拟，即利用具有代表性的采样样本平均来代替系统的系综平均。具有代表性的例子就是经典二维Ising模型的模拟，通过对采样样本的平均推断出临界温度。
​
这篇文章利用机器学习中监督学习的神经网络模型，配合蒙特卡洛模拟进行验证，对二维模型展开研究。
​
在文章的一开始构建了判断二维正方形格子Ising模型$H=-J{\sum }_{(ij)}{\sigma }_i^z{\sigma }_j^z$是否磁化的神经网络。利用蒙特卡洛模拟得到的自旋构型作为神经网络的输入层输入变量，输出层有两个输出变量：总体磁化，或总体无磁化（这两个变量可以用来判断样本处于临界温度之上或之下）。在输入层和输出层之间还有一百个神经元组成的隐藏层。通过大量的训练样本训练，该神经网络可以对输入的样本进行分类，即输入样本是否磁化，进而判断出二维正方形格子Ising模型的临界温度为$T_{\mathrm{c}}/J\simeq 2.266\pm 0.002$，与理论值$T_{\mathrm{c}}/J=2/\ln (1+\sqrt{2})\approx 2.269$十分接近。因此利用该神经网络可以对输入自旋构型进行分类，进而判断模型的临界温度。
​
研究人员发现，该神经网络虽然是利用正方形格子模型作为神经网络的训练集，但却仍然可以适用于判断其他形状格子Ising模型的自旋构型。文中用同样的神经网络，对三角格子Ising模型进行研究，得到三角格子模型的临界温度约为$T_{\mathrm{c}}/J\simeq 3.65\pm 0.01$，与实际数值$T_{\mathrm{c}}/J=4/\ln 3\approx 3.641$十分接近。这个结果是十分有趣的，因为虽然神经网络的训练集是正方格子，但训练得到的神经网络却不仅可适用于正方格子，还适用于其他形状的模型。通过神经网络得到分类模型具有一定的推广性。
​
后文对凝聚态体系中的无序态与拓扑相展开了具体研究，由于本次作业时间有限，不在此展开。
​

5. 总结

神经网络模型是处理大量数据非线性拟合十分有效的工具。在凝聚态物理系统，由于研究对象是十分庞大的，因此往往拥有大量的研究数据，此时利用神经网络来处理分析这些研究数据，并以此进行预测是十分有效的。

---

参考文献

1. 吴恩达（Andrew Ng）机器学习课程。
2. Carnegie Mellon University, Introduction to Deep Learning
3. Carrasquilla, J., Melko, R. Machine learning phases of matter. Nature Phys 13, 431–434 (2017). https://doi.org/10.1038/nphys4035

周先亮

2020/05/29