深度学习笔记四：MNIST实战

这里的实战是根据Neural Networks and Deep Learning的前两章整理出来的。用了它提供的数据集以及一些代码。然后自己修改了他的一些代码，使得更加容易理解。

一.任务及数据

就是自己写一个神经网络来实现对于MNIST数据集的手写体分类任务。作者提供了一个数据集，这里就使用作者的数据集。
MNIST数据集
下载下来直接放在工程目录里面就行了。
训练(train) : 50,000
验证(validation): 10,000
测试(test): 10,000
从任务和输入就能够得到大概的网络结构：

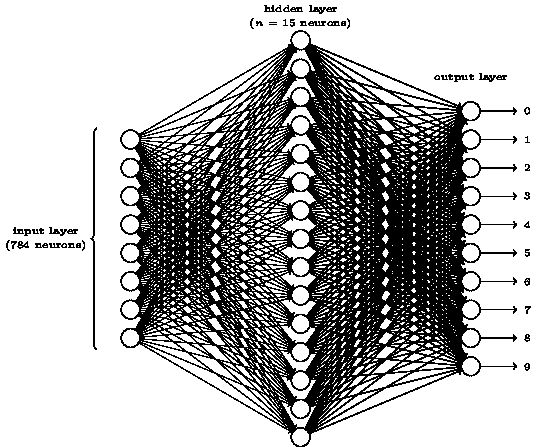
损失函数为二次误差函数
激活函数为sigmoid函数。

二.读取数据

读取数据由mnist_loader.py这个文件实现。
代码:

# -*- coding: utf-8 -*- 
from __future__ import print_function,division
import pickle
import gzip
import numpy as np

#从数据集中载入数据
def load_data():
    file=gzip.open('mnist.pkl.gz','rb')
    training_data,validation_data,test_data=pickle.load(file)
    file.close()
    return training_data,validation_data,test_data

#改编数据集的格式
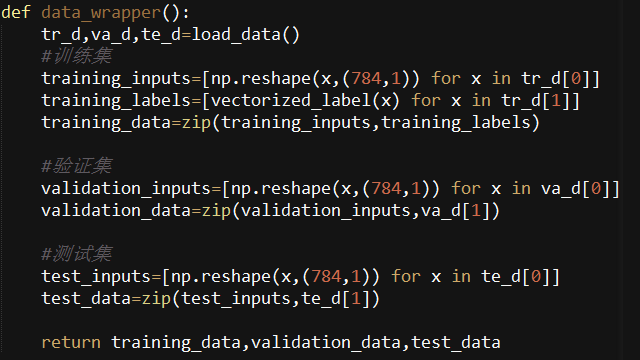
def data_wrapper():
    tr_d,va_d,te_d=load_data()
    #训练集
    training_inputs=[np.reshape(x,(784,1)) for x in tr_d[0]]
    training_labels=[vectorized_label(x) for x in tr_d[1]]
    training_data=zip(training_inputs,training_labels)

    #验证集
    validation_inputs=[np.reshape(x,(784,1)) for x in va_d[0]]
    validation_data=zip(validation_inputs,va_d[1])

    #测试集
    test_inputs=[np.reshape(x,(784,1)) for x in te_d[0]]
    test_data=zip(test_inputs,te_d[1])

    return training_data,validation_data,test_data

def vectorized_label(j):
    #形状为10行1列
    e=np.zeros((10,1))
    e[j]=1.0
    return e

代码解释:
1.load_data函数

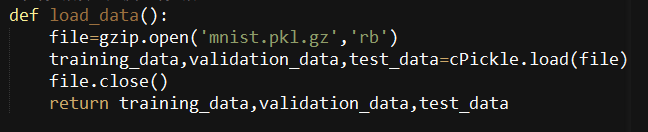
Load_data()主要作用:解压数据集,然后从数据集中把数据取出来.
然后取出来之后的几个变量代表的数据的格式分别是这样的:

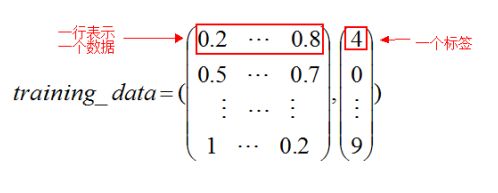
training_data:是一个由两个元素构成的元组.
其中一个元素是测试图片集合,是一个50000*784的numpy ndarray(其中50000行就是数据的数量,784列就是一个数据的维度(这里是像素)).
第二个元素就是一个测试图片的标签集.是一个50000*1的numpy ndarray.其中指明了每行是一个什么数字…通俗的来说就是这个样子:

validation_data和test_data的结构和上面的training_data是一样的,只是数量(元素的行数)不一样.这两个是10000行.

2.load_data_wrapper函数

之前的load_data返回的格式虽然很漂亮,但是并不是非常适合我们这里计划的神经网络的结构,因此我们在load_data的基础上面使用load_data_wrapper函数来进行一点点适当的数据集变换,使得数据集更加适合我们的神经网络训练.
以训练集的变换为例
对于training_inputs来说,就是把之前的返回的training_data[0]的所有例子都放到了一个列表中:
简单的来说如下图所示

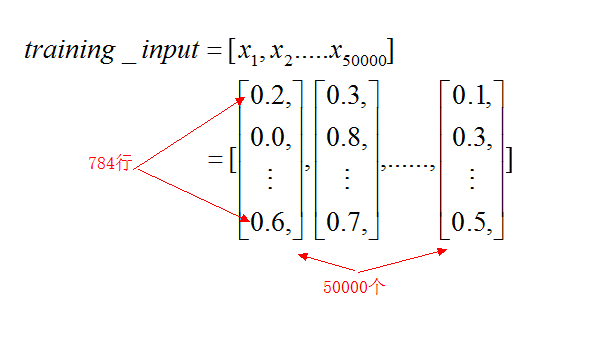
同样可以知道training_labels的样子为

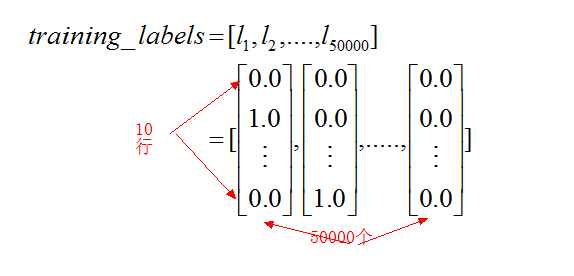
然后training_data为zip函数组合,那么training_data为一个列表,其中每个元素是一个元组,二元组又有一个training_inputs和一个training_labels的元素组合而成.如下图

同理可以推出其他数据的形状

二.神经网络部分

完整代码：

# -*- coding: utf-8 -*- 
import random
import numpy as np 

#sigmoid函数
def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))
#sigmoid函数的导数
def sigmoid_prime(z):
    return sigmoid(z)*(1-sigmoid(z))

#神经网络的类
class Network(object):
    #构造函数初始化网络
    def __init__(self,sizes):
        self.numOfLayers=len(sizes)
        self.sizes=sizes
        #随机初始化偏置和权重
        self.biases=[np.random.randn(i,1) for i in sizes[1:]]
        self.weights=[np.random.randn(j,i) for i,j in zip(sizes[:-1],sizes[1:])]

    #前向传播
    def feedforward(self,a):
        for w,b in zip(self.weights,self.biases):
            a=sigmoid(np.dot(w,a)+b)
        return a 

    #随机梯度下降(训练数据,迭代次数,小样本数量,学习率,是否有测试集)
    def SGD(self,training_data,epochs,mini_batch_size,learning_rate,test_data=None):
        if test_data:
            len_test=len(test_data)
        n=len(training_data)  #训练数据大小
        #迭代过程
        for j in range(epochs):
            print "Epoch {0}:".format(j)
            random.shuffle(training_data)
            #mini_batches是列表中放切割之后的列表
            mini_batches=[training_data[k:k+mini_batch_size] for k in range(0,n,mini_batch_size)]
            #每个mini_batch都更新一次,重复完整个数据集
            for mini_batch in mini_batches:
                #存储C对于各个参数的偏导
                #格式和self.biases和self.weights是一模一样的
                nabla_b=[np.zeros(b.shape) for b in self.biases]
                nabla_w=[np.zeros(w.shape) for w in self.weights]
                eta=learning_rate/len(mini_batch)
                #mini_batch中的一个实例调用梯度下降得到各个参数的偏导
                for x,y in mini_batch:
                    #从一个实例得到的梯度
                    delta_nabla_b,delta_nabla_w=self.backprop(x,y)
                    nabla_b=[nb+dnb for nb,dnb in zip(nabla_b,delta_nabla_b)]
                    nabla_w=[nw+dnw for nw,dnw in zip(nabla_w,delta_nabla_w)]
                #每一个mini_batch更新一下参数
                self.biases=[b-eta*nb for b,nb in zip(self.biases,nabla_b)]
                self.weights=[w-eta*nw for w,nw in zip(self.weights,nabla_w)]

            if test_data:
                print "{0}/{1}".format(self.evaluate(test_data),len_test)


    #反向传播(对于每一个实例)
    def backprop(self,x,y):
        #存储C对于各个参数的偏导
        #格式和self.biases和self.weights是一模一样的
        nabla_b=[np.zeros(b.shape) for b in self.biases]
        nabla_w=[np.zeros(w.shape) for w in self.weights]

        #前向过程
        activation=x
        activations=[x] #存储所有的激活值,一层一层的形式
        zs=[]   #存储所有的中间值(weighted sum)
        for w,b in zip(self.weights,self.biases):
            z=np.dot(w,activation)+b
            zs.append(z)
            activation=sigmoid(z)
            activations.append(activation)

        #反向过程
        #输出层error
        delta=self.cost_derivative(activations[-1],y)*sigmoid_prime(zs[-1])
        nabla_b[-1]=delta
        nabla_w[-1]=np.dot(delta,activations[-2].transpose())

        #非输出层
        for l in range(2,self.numOfLayers):
            delta=np.dot(self.weights[-l+1].transpose(),delta)*sigmoid_prime(zs[-l])
            nabla_b[-l]=delta
            nabla_w[-l]=np.dot(delta,activations[-l-1].transpose())

        return nabla_b,nabla_w

    #输出层cost函数对于a的导数
    def cost_derivative(self,output_activations,y):
        return output_activations-y

    def evaluate(self,test_data):
        test_result=[(np.argmax(self.feedforward(x)),y) for (x,y) in test_data]
        return sum(int(i==j) for (i,j) in test_result)