深度学习一:搭建简单的全连接神经网络
深度学习一:搭建简单的全连接神经网络
新手入门学习神经网络,尝试搭建浅层的全连接神经网络,废话不多说,上主题(文章左后会贴上全部代码):
实验环境:Python3+Pycharm
一个神经网络分为输入层、隐藏和输出层,先实现一个单隐藏层的神经网络,输入为随机向量x,通过神经网络,拟合随机向量y。将神经网络的训练拆成两部分,即向前传播和反向传播,分别用函数实现。
首先是引入:
import numpy as np
import matplotlib.pyplot as plt使用numpy来做多种运算,使用matplotlib来画图
向前传播:
输入input向量x、参数w1、w2和偏置b1、b2,z1是隐藏层的中间输出,A1是经过sigmoid激活后的输出。将A1送入输入层,输出的A2便是最终输出。
假定输入x的维度为n*m,w1的维度为h*n(表示该层的神经元为h个),w2的维度为1*h,最终输出的A2维度为1*m。使用numpy中的dot()函数来做矩阵运算。
def forward(X, w1, w2, b1, b2):
z1 = np.dot(w1, X) + b1 # w1=h*n X=n*m z1=h*m
A1 = sigmoid(z1) # A1=h*m
z2 = np.dot(w2, A1) + b2 # w2=1*h z2=1*m
A2 = sigmoid(z2) # A2=1*m
return z1, z2, A1, A2这里需要先定义一下激活函数:
def sigmoid(z):
return 1 / (1 + np.exp(-z))反向传播:
计算参数的偏导数
def backward(y, X, A2, A1, z2, z1, w2, w1):
n, m = np.shape(X)
dz2 = A2 - y # A2=1*m y=1*m
dw2 = 1 / m * np.dot(dz2, A1.T) # dz2=1*m A1.T=m*h dw2=1*h
db2 = 1 / m * np.sum(dz2, axis=1, keepdims=True)
dz1 = np.dot(w2.T, dz2) * A1 * (1 - A1) # w2.T=h*1 dz2=1*m z1=h*m A1=h*m dz1=h*m
dw1 = 1 / m * np.dot(dz1, X.T) # z1=h*m X'=m*n dw1=h*n
db1 = 1 / m * np.sum(dz1, axis=1, keepdims=True)
return dw1, dw2, db1, db2定义完了训练的向前传播和反向传播,还需要定义一个损失函数:
def costfunction(A2, y):
m, n = np.shape(y)
J = np.sum(y * np.log(A2) + (1 - y) * np.log(1 - A2)) / m
# J = (np.dot(y, np.log(A2.T)) + np.dot((1 - y).T, np.log(1 - A2))) / m
return -Jok,到这里一个神经网络的框架基本有了,在开始训练之前,还需要定义一下各个参数并初始化。
首先是输入x和拟合数据y:
X=np.random.rand(100,200)
n, m = np.shape(X)
y=np.random.rand(1,m)由于是初步搭建,这里的x和y均采用随机变量,大概体验一下神经网络即可。随机初试化一个维度为[100,200]的x和[1,200]的y。
接下来,定义各个参数:
n_x = n # size of the input layer
n_y = 1 # size of the output layer
n_h = 5 # size of the hidden layer
w1 = np.random.randn(n_h, n_x) * 0.01 # h*n
b1 = np.zeros((n_h, 1)) # h*1
w2 = np.random.randn(n_y, n_h) * 0.01 # 1*h
b2 = np.zeros((n_y, 1))
alpha = 0.1
number = 10000定义隐藏层的神经元个数为5,随机初始化w1、w2、b1和b2,定义学习率alpha为0.1,迭代次数为10000
之后,便可以开始训练了:
for i in range(0, number):
z1, z2, A1, A2 = forward(X, w1, w2, b1, b2)
dw1, dw2, db1, db2 = backward(y, X, A2, A1, z2, z1, w2, w1)
w1 = w1 - alpha * dw1
w2 = w2 - alpha * dw2
b1 = b1 - alpha * db1
b2 = b2 - alpha * db2
J = costfunction(A2, y)
if (i % 100 == 0):
print(i)
plt.plot(i, J, 'ro')
plt.show()使用梯度下降的方法来最小化损失函数,每次迭代后,描点损失函数J的值。
全部代码如下:
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def forward(X, w1, w2, b1, b2):
z1 = np.dot(w1, X) + b1 # w1=h*n X=n*m z1=h*m
A1 = sigmoid(z1) # A1=h*m
z2 = np.dot(w2, A1) + b2 # w2=1*h z2=1*m
A2 = sigmoid(z2) # A2=1*m
return z1, z2, A1, A2
def backward(y, X, A2, A1, z2, z1, w2, w1):
n, m = np.shape(X)
dz2 = A2 - y # A2=1*m y=1*m
dw2 = 1 / m * np.dot(dz2, A1.T) # dz2=1*m A1.T=m*h dw2=1*h
db2 = 1 / m * np.sum(dz2, axis=1, keepdims=True)
dz1 = np.dot(w2.T, dz2) * A1 * (1 - A1) # w2.T=h*1 dz2=1*m z1=h*m A1=h*m dz1=h*m
dw1 = 1 / m * np.dot(dz1, X.T) # z1=h*m X'=m*n dw1=h*n
db1 = 1 / m * np.sum(dz1, axis=1, keepdims=True)
return dw1, dw2, db1, db2
def costfunction(A2, y):
m, n = np.shape(y)
J = np.sum(y * np.log(A2) + (1 - y) * np.log(1 - A2)) / m
# J = (np.dot(y, np.log(A2.T)) + np.dot((1 - y).T, np.log(1 - A2))) / m
return -J
# Data = np.loadtxt("gua2.txt")
# X = Data[:, 0:-1]
# X = X.T
# y = Data[:, -1]
X=np.random.rand(100,200)
n, m = np.shape(X)
y=np.random.rand(1,m)
#y = y.reshape(1, m)
n_x = n # size of the input layer
n_y = 1 # size of the output layer
n_h = 5 # size of the hidden layer
w1 = np.random.randn(n_h, n_x) * 0.01 # h*n
b1 = np.zeros((n_h, 1)) # h*1
w2 = np.random.randn(n_y, n_h) * 0.01 # 1*h
b2 = np.zeros((n_y, 1))
alpha = 0.1
number = 10000
for i in range(0, number):
z1, z2, A1, A2 = forward(X, w1, w2, b1, b2)
dw1, dw2, db1, db2 = backward(y, X, A2, A1, z2, z1, w2, w1)
w1 = w1 - alpha * dw1
w2 = w2 - alpha * dw2
b1 = b1 - alpha * db1
b2 = b2 - alpha * db2
J = costfunction(A2, y)
if (i % 100 == 0):
print(i)
plt.plot(i, J, 'ro')
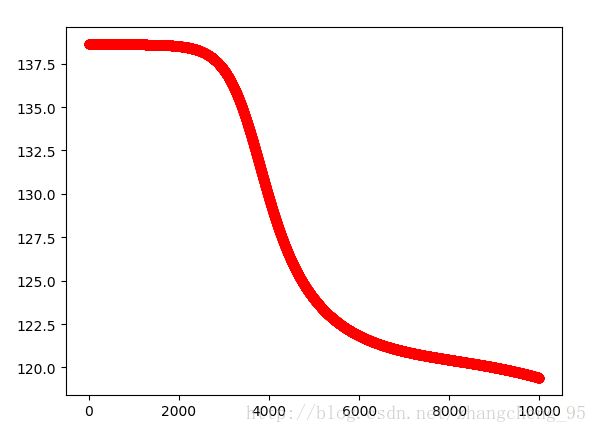
plt.show()运行后的实验结果:
可以看到随着迭代次数的增加,损失函数是逐渐减小的。
补充(稍加改进版):
在原有的基础上,加入一层隐藏层:
补充定义:
n_x=n
n_y=1
n_h1=5
n_h2=4
W1=np.random.rand(n_x,n_h1)*0.01
W2=np.random.rand(n_h1,n_h2)*0.01
W3=np.random.rand(n_h2,n_y)*0.01
b1=np.zeros((n_h1,1))
b2=np.zeros((n_h2,1))
b3=np.zeros((n_y,1))将新的隐藏层的神经元个数定义n_h2=4
向前传播:
# 向前传递
def forward(X, W1, W2, W3, b1, b2, b3):
# 隐藏层1
Z1 = np.dot(W1.T,X)+b1 # X=n*m ,W1.T=h1*n,b1=h1*1,Z1=h1*m
A1 = sigmoid(Z1) # A1=h1*m
# 隐藏层2
Z2 = np.dot(W2.T, A1) + b2 # W2.T=h2*h1,b2=h2*1,Z2=h2*m
A2 = sigmoid(Z2) # A2=h2*m
# 输出层
Z3=np.dot(W3.T,A2)+b3 # W3.T=(h3=1)*h2,b3=(h3=1)*1,Z3=1*m
A3=sigmoid(Z3) # A3=1*m
return Z1,Z2,Z3,A1,A2,A3反向传播:
# 反向传播
def backward(Y,X,A3,A2,A1,Z3,Z2,Z1,W3,W2,W1):
n,m = np.shape(X)
dZ3 = A3-Y # dZ3=1*m
dW3 = 1/m *np.dot(A2,dZ3.T) # dW3=h2*1
db3 = 1/m *np.sum(dZ3,axis=1,keepdims=True) # db3=1*1
dZ2 = np.dot(W3,dZ3)*A2*(1-A2) # dZ2=h2*m
dW2 = 1/m*np.dot(A1,dZ2.T) #dw2=h1*h2
db2 = 1/m*np.sum(dZ2,axis=1,keepdims=True) #db2=h2*1
dZ1 = np.dot(W2, dZ2) * A1 * (1 - A1) # dZ1=h1*m
dW1 = 1 / m * np.dot(X, dZ1.T) # dW1=n*h
db1 = 1 / m * np.sum(dZ1,axis=1,keepdims=True) # db1=h*m
return dZ3,dZ2,dZ1,dW3,dW2,dW1,db3,db2,db1for i in range(0,number):
Z1,Z2,Z3,A1,A2,A3=forward(X,W1,W2,W3,b1,b2,b3)
dZ3, dZ2, dZ1, dW3, dW2, dW1, db3, db2, db1=backward(Y,X,A3,A2,A1,Z3,Z2,Z1,W3,W2,W1)
W1=W1-alpha*dW1
W2=W2-alpha*dW2
W3=W3-alpha*dW3
b1=b1-alpha*db1
b2=b2-alpha*db2
b3=b3-alpha*db3
J=costfunction(Y,A3)可以说改动不是很大,如果需要更深层次的神经网络,按这个方法添加就可以了,当然,如果层次太多,代码还是显得太过繁琐。
修改后的全部代码如下:
import numpy as np
import matplotlib.pyplot as plt
# 激活函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 向前传递
def forward(X, W1, W2, W3, b1, b2, b3):
# 隐藏层1
Z1 = np.dot(W1.T,X)+b1 # X=n*m ,W1.T=h1*n,b1=h1*1,Z1=h1*m
A1 = sigmoid(Z1) # A1=h1*m
# 隐藏层2
Z2 = np.dot(W2.T, A1) + b2 # W2.T=h2*h1,b2=h2*1,Z2=h2*m
A2 = sigmoid(Z2) # A2=h2*m
# 输出层
Z3=np.dot(W3.T,A2)+b3 # W3.T=(h3=1)*h2,b3=(h3=1)*1,Z3=1*m
A3=sigmoid(Z3) # A3=1*m
return Z1,Z2,Z3,A1,A2,A3
# 反向传播
def backward(Y,X,A3,A2,A1,Z3,Z2,Z1,W3,W2,W1):
n,m = np.shape(X)
dZ3 = A3-Y # dZ3=1*m
dW3 = 1/m *np.dot(A2,dZ3.T) # dW3=h2*1
db3 = 1/m *np.sum(dZ3,axis=1,keepdims=True) # db3=1*1
dZ2 = np.dot(W3,dZ3)*A2*(1-A2) # dZ2=h2*m
dW2 = 1/m*np.dot(A1,dZ2.T) #dw2=h1*h2
db2 = 1/m*np.sum(dZ2,axis=1,keepdims=True) #db2=h2*1
dZ1 = np.dot(W2, dZ2) * A1 * (1 - A1) # dZ1=h1*m
dW1 = 1 / m * np.dot(X, dZ1.T) # dW1=n*h
db1 = 1 / m * np.sum(dZ1,axis=1,keepdims=True) # db1=h*m
return dZ3,dZ2,dZ1,dW3,dW2,dW1,db3,db2,db1
def costfunction(Y,A3):
m, n = np.shape(Y)
J=np.sum(Y*np.log(A3)+(1-Y)*np.log(1-A3))/m
# J = (np.dot(y, np.log(A2.T)) + np.dot((1 - y).T, np.log(1 - A2))) / m
return -J
# Data = np.loadtxt("gua2.txt")
# X = Data[:, 0:-1]
# X = X.T
# Y = Data[:, -1]
# Y=np.reshape(1,m)
X=np.random.rand(100,200)
n,m=np.shape(X)
Y=np.random.rand(1,m)
n_x=n
n_y=1
n_h1=5
n_h2=4
W1=np.random.rand(n_x,n_h1)*0.01
W2=np.random.rand(n_h1,n_h2)*0.01
W3=np.random.rand(n_h2,n_y)*0.01
b1=np.zeros((n_h1,1))
b2=np.zeros((n_h2,1))
b3=np.zeros((n_y,1))
alpha=0.1
number=10000
for i in range(0,number):
Z1,Z2,Z3,A1,A2,A3=forward(X,W1,W2,W3,b1,b2,b3)
dZ3, dZ2, dZ1, dW3, dW2, dW1, db3, db2, db1=backward(Y,X,A3,A2,A1,Z3,Z2,Z1,W3,W2,W1)
W1=W1-alpha*dW1
W2=W2-alpha*dW2
W3=W3-alpha*dW3
b1=b1-alpha*db1
b2=b2-alpha*db2
b3=b3-alpha*db3
J=costfunction(Y,A3)
if (i%100==0):
print(i)
plt.plot(i,J,'ro')
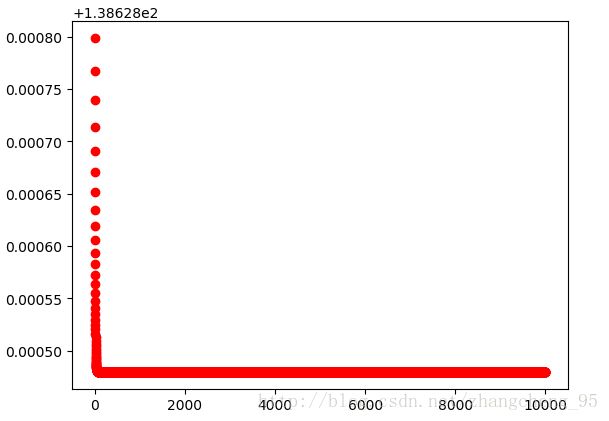
plt.show()运行结果:
可以看到这个损失函数的下降就比较快了,因为只是简单的随机数据,两层的神经网络相对来说也比较“深”了。