从零开始写光栅化渲染器2:直线绘制光栅化算法
直线绘制光栅化算法
1.数值微分DDA(Digital Differential Analyzer)算法
1.1原理
引入增量思想,以dx≥dy(斜率[0,1])为例,考虑直线y=kx+b,当x步进为1时,y步进为k,即yi+1=yi+k,根据四舍五入法即可绘制直线
1.2伪代码
y = y1;
for(x:[x1,x2])
{
drawPixel(x,y);
y += k;
}1.3实现代码
/************************************************************************/
/* 数值微分DDA(Digital Differential Analyzer)算法 */
/************************************************************************/
void drawline(int x1,int y1,int x2,int y2,acolor color)
{
int dx = abs(x2 - x1);
int dy = abs(y2 - y1);
if (dx>=dy) //以dx=1为步进,否则会出现断点
{
if (x1>x2)
{
swap(x1,x2);
swap(y1,y2);
}
float k = static_cast<float>(y2-y1)/(x2-x1);
float y = y1;
for (int x=x1;x<=x2;++x)
{
drawpixel(x,y,color);
y += k;
}
}
else
{
if (y1>y2)
{
swap(x1,x2);
swap(y1,y2);
}
float k = static_cast<float>(x2-x1)/(y2-y1);
float x = x1;
for (int y=y1;y<=y2;++y)
{
drawpixel(x,y,color);
x += k;
}
}
}DDA算法原理简单明了,但是由于存在浮点数的加减运算,所以效率还需提高。
2.中点画线算法
2.1原理
通过一般式Ax+By+C=0来绘制直线,同样考虑斜率[0,1]情况,对于任意一点P(x,y)我们可以通过B(Ax+By+C)的正负来判断点P相对于直线的位置,>0时点在直线的上方,=0则在直线上,<0则在直线下方。根据这个原理,我们可以通过判断点(xi+1,yi+0.5)相对于直线的位置来进行直线取点。
我们把中点代入f(x,y)
d0=f(xi+1,yi+0.5)=Axi+Byi+C+A+0.5B=A+0.5B
若取上点,则
d1=f(xi+2,yi+1.5)=d0+A+B
若取下点,则
d1=f(xi+2,yi+0.5)=d0+A
这里我们可以将d乘以2以消除浮点数,避免浮点数运算的开销,提高运算效率
2.2伪代码
d = 2A+B;
y = y1;
for(x:[x1,x2])
{
drawPixel(x,y);
if(d<0) //中点在直线下方,取上点
{
d += 2(A+B);
++y;
}
else
{
d += 2A;
}
}2.3实现代码
/************************************************************************/
/* 绘制直线(中点法)
* 隐式方程f(x,y)=(y1-y1)x+(x2-x1)y+x1y2-x2y1=0
* B*f(x,y)>0为上,<0为下,每次用中点(x+1,y±0.5)带入进行比较
* 此处取B>0,即可直接判断
*/
/************************************************************************/
void drawLine(int x1,int y1,int x2,int y2,AColor color)
{
int dx = abs(x2 - x1);
int dy = abs(y2 - y1);
if (dx>=dy) //以dx=1为步进,否则会出现断点
{
if (x1>x2)
{
swap(x1,x2);
swap(y1,y2);
}
int A = y1-y2;
int B = x2-x1;
if(y2>=y1) //斜率[0,1]
{
int d = (A<<1) + B; //f(x+1,y+0.5)*2以消除浮点数运算
int upIncrement = (A+B)<<1; //取上点时d的增量
int downTncrement = A<<1; //取下点时d的增量
for (int x=x1,y=y1;x<=x2;++x)
{
drawPixel(x,y,color);
if (d<0){ //中点在直线下,取上点
d += upIncrement;
++y;
}
else
{
d += downTncrement;
}
}
}
else //斜率[-1,0)
{
int d = (A<<1) - B;
int upIncrement = A<<1;
int downTncrement = (A-B)<<1;
for (int x=x1,y=y1;x<=x2;++x)
{
drawPixel(x,y,color);
if (d<0){
d += upIncrement;
}
else
{
d += downTncrement;
--y;
}
}
}
}
else
{
if (y1>y2)
{
swap(x1,x2);
swap(y1,y2);
}
int A = x1-x2;
int B = y2-y1;
if (x2>=x1)
{
int d = (A<<1) + B; //f(x+0.5,y+1)*2以消除浮点数运算,此处Ay+Bx+C=0
int upIncrement = (A+B)<<1; //取上点时d的增量
int downTncrement = A<<1; //取下点时d的增量
for (int x=x1,y=y1;y<=y2;++y)
{
drawPixel(x,y,color);
if (d<0){ //中点在直线下,取上点
d += upIncrement;
++x;
}
else
{
d += downTncrement;
}
}
}
else
{
int d = (A<<1) - B;
int upIncrement = A<<1;
int downTncrement = (A-B)<<1;
for (int x=x1,y=y1;y<=y2;++y)
{
drawPixel(x,y,color);
if (d<0){
d += upIncrement;
}
else
{
d += downTncrement;
--x;
}
}
}
}
}3.Bresenham算法
3.1原理
同样从简单的开始考虑(斜率[0,1]),当x步进1时,y提高k,则我们用d记录提高量,一旦d>0.5,我们便取上点,并对d进行减1操作。同样,这样也会出现浮点数加减法运算,首先我们可以通过e=d-0.5的正负来进行判断,因为对d-0.5的正乘法不会影响其符号,所以我们可以进行如下改变:
第一步:(d-0.5)*2 = 2d-1,消除0.5这个浮点数。
由于d=dy/dx(dy=y2-y1,dx=x2-x1)同样会产生浮点数,因为斜率为[0,1],所以我们可以保证dx>0
第二步:(2d-1)*dx = 2dy-dx,此时浮点数完全被消除。
3.2伪代码
k = 2dy;
e = -dx;
for(x:[x1,x2])
{
drawPixel(x,y);
e += k;
if(e>0)
{
++y;
e -= 2dx;
}
}3.3实现代码
/************************************************************************/
/* Bresenham算法
* 主要通过e=d±0.5判断符号
*/
/************************************************************************/
void drawLine(int x1,int y1,int x2,int y2,AColor color)
{
int dx = abs(x2 - x1);
int dy = abs(y2 - y1);
if (dx>=dy) //以dx=1为步进,否则会出现断点
{
if (x1>x2)
{
swap(x1,x2);
swap(y1,y2);
}
int flag = y2>=y1?1:-1; //斜率[-1,1]
int k = flag*(dy<<1);
int e = -dx*flag;
for (int x=x1,y=y1;x<=x2;++x)
{
drawPixel(x,y,color);
e += k;
if (flag*e>0)
{
y += flag;
e -= 2*dx*flag;
}
}
}
else
{
if (y1>y2)
{
swap(x1,x2);
swap(y1,y2);
}
int flag = x2>x1?1:-1;
int k = flag*(dx<<1);
int e = -dy*flag;
for (int x=x1,y=y1;y<=y2;++y)
{
drawPixel(x,y,color);
e += k;
if (flag*e>0)
{
x += flag;
e -= 2*dy*flag;
}
}
}
}
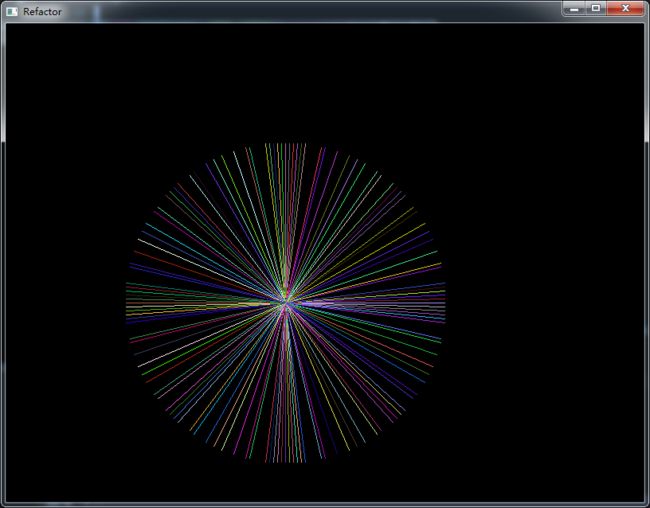
4.效果图
绘制一个圆中的一些半径,圆心(350,350)
for (int i=0;i<580;i+=5)
{
for (int j=0;j<580;j+=5)
{
double v = sqrt(pow(i-350,2)+pow(j-350,2))-200;
if ( v>=0&&v < 2)
{
drawline(350,350,i,j,AColor(0,(1+rand()%255)/255.0f,(1+rand()%255)/255.0f,(1+rand()%255)/255.0f));
}
}
}项目完整地址:
3DRender: https://github.com/zhanghuanzj/3DRender.git