斯坦福CS231n课程笔记纯干货1

CS231n的全称是CS231n: Convolutional Neural Networks for Visual Recognition，即面向视觉识别的卷积神经网络。该课程是斯坦福大学计算机视觉实验室推出的课程。目前大家说CS231n，大都指的是2016年冬季学期（一月到三月）的版本。

1. 分类器中L1和L2比较。

在面对两个向量之间的差异时，L2比L1更加不能容忍这些差异，相对于1个巨大的差异，L2距离更倾向于接受多个中等程度的差异。

2. k-Nearest Neighbor分类器存在以下不足

分类器必须记住所有训练数据并将其存储起来，以便于未来测试数据用于比较。这在存储空间上是低效的，数据集的大小很容易就以GB计。对一个测试图像进行分类需要和所有训练图像作比较，算法计算资源耗费高。

Nearest Neighbor分类器在某些特定情况（比如数据维度较低）下，可能是不错的选择。但是在实际的图像分类工作中，很少使用。

实际应用流程：

1) 预处理你的数据：对你数据中的特征进行归一化（normalize），让其具有零平均值（zeromean）和单位方差（unit variance）。

2) 如果数据是高维数据，考虑使用降维方法，比如PCA或随机投影。

3) 将数据随机分入训练集和验证集。按照一般规律，70%-90% 数据作为训练集。如果需要预测的超参数很多，那么就应该使用更大的验证集来有效地估计它们。如果担心验证集数量不够，那么就尝试交叉验证方法。

4) 在验证集上调优，尝试足够多的k值，尝试L1和L2两种范数计算方式。

5) 如果分类器跑得太慢，尝试使用Approximate Nearest Neighbor库（比如FLANN）来加速这个过程，其代价是降低一些准确率。

6) 对最优的超参数做记录。千万不要在最终的分类器中使用验证集数据，这样做会破坏对于最优参数的估计。直接使用测试集来测试用最优参数设置好的最优模型，得到测试集数据的分类准确率，并以此作为你的kNN分类器在该数据上的性能表现。

3. 验证集、交叉验证集和超参数调优

特别注意：决不能使用测试集来进行调优。测试数据集只使用一次，即在训练完成后评价最终的模型时使用。调优策略从训练集中取出一部分数据用来调优，我们称之为验证集（validation set）。把训练集分成训练集和验证集。使用验证集来对所有超参数调优。最后只在测试集上跑一次并报告结果。

交叉验证：

常用的数据分割模式。给出训练集和测试集后，训练集一般会被均分。这里是分成5份。前面4份用来训练，黄色那份用作验证集调优。如果采取交叉验证，那就各份轮流作为验证集。最后模型训练完毕，超参数都定好了，让模型跑一次（而且只跑一次）测试集，以此测试结果评价算法。

4. 线性分类器

将图像看做高维度的点：既然图像被伸展成为了一个高维度的列向量，那么我们可以把图像看做这个高维度空间中的一个点（即每张图像是3072维空间中的一个点）。整个数据集就是一个点的集合，每个点都带有1个分类标签。

如下图，图像空间的示意图。其中每个图像是一个点，有3个分类器。以红色的汽车分类器为例，红线表示空间中汽车分类分数为0的点的集合，红色的箭头表示分值上升的方向。所有红线右边的点的分数值均为正，且线性升高。红线左边的点分值为负，且线性降低。

5. 损失函数

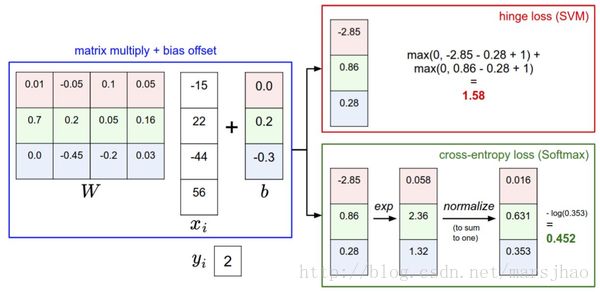
多类支持向量机损失Multiclass Support Vector Machine Loss

第i个数据中包含图像的像素和代表正确类别的标签。评分函数输入像素数据，然后通过公式来计算不同分类类别的分值。这里我们将分值简写为s。比如，针对第j个类别的得分就是第j个元素：。针对第i个数据的多类SVM的损失函数定义如下：

SVM的损失函数想要正确分类类别的分数比不正确类别分数高，而且至少要高。如果不满足这点，就开始计算损失值。

正则化（Regularization）

我们希望能向某些特定的权重W添加一些偏好，对其他权重则不添加，以此来消除模糊性。这一点是能够实现的，方法是向损失函数增加一个正则化惩罚（regularization penalty）R(W)部分。最常用的正则化惩罚是L2范式，L2范式通过对所有参数进行逐元素的平方惩罚来抑制大数值的权重：

包含正则化惩罚后，就能够给出完整的多类SVM损失函数了，它由两个部分组成：数据损失（data loss），即所有样例的的平均损失Li，以及正则化损失（regularization loss）。完整公式如下所示：

将其展开完整公式是：

Softmax分类器

交叉熵损失（cross-entropy loss）。公式如下：

 或等价的 

在上式中，使用fj来表示分类评分向量f中的第j个元素。

SVM和Softmax的比较

Softmax分类器为每个分类提供了“可能性”。 softmax分类器算出来的概率最好是看成一种对于分类正确性的自信。和SVM一样，数字间相互比较得出的大小顺序是可以解释的，但其绝对值则难以直观解释。softmax分类器对于分数是永远不会满意的：正确分类总能得到更高的可能性，错误分类总能得到更低的可能性，损失值总是能够更小。但是，SVM只要边界值被满足了就满意了，不会超过限制去细微地操作具体分数。这可以被看做是SVM的一种特性。

更多关注：MNIST在TensorFlow上的Softmax回归模型实现

6. 梯度下降

梯度下降是对神经网络的损失函数最优化中最常用的方法。

小批量数据梯度下降（Mini-batch gradient descent）：在大规模的应用中（比如ILSVRC挑战赛），训练数据可以达到百万级量级。如果像这样计算整个训练集，来获得仅仅一个参数的更新就太浪费了。一个常用的方法是计算训练集中的小批量（batches）数据。

7. 梯度反向传播

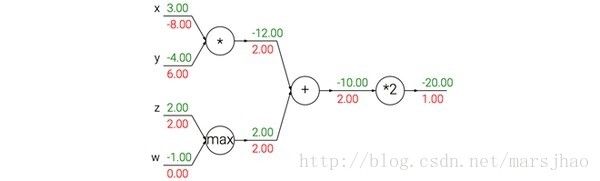
加法门单元把输出的梯度相等地分发给它所有的输入，这一行为与输入值在前向传播时的值无关。这是因为加法操作的局部梯度都是简单的+1，所以所有输入的梯度实际上就等于输出的梯度，因为乘以1.0保持不变。上例中，加法门把梯度2.00不变且相等地路由给了两个输入。

取最大值门单元对梯度做路由。和加法门不同，取最大值门将梯度转给其中一个输入，这个输入是在前向传播中值最大的那个输入。这是因为在取最大值门中，最高值的局部梯度是1.0，其余的是0。上例中，取最大值门将梯度2.00转给了z变量，因为z的值比w高，于是w的梯度保持为0。

乘法门单元相对不容易解释。它的局部梯度就是输入值，但是是相互交换之后的，然后根据链式法则乘以输出值的梯度。上例中，x的梯度是-4.00x2.00=-8.00。

8. 神经网络基本概念

一个两层的神经网络计算公式是

非线性函数在神经网络的计算上是至关重要的，如果略去这一步，那么两个矩阵将会合二为一，对于分类的评分计算将重新变成关于输入的线性函数。

二分类Softmax分类器。举例来说，可以把看做其中一个分类的概率，其他分类的概率为，因为它们加起来必须为1。根据这种理解，可以得到交叉熵损失。然后将它最优化为二分类的Softmax分类器（也就是逻辑回归）。

二分类SVM分类器。或者可以在神经元的输出外增加一个最大边界折叶损失（max-margin hinge loss）函数，将其训练成一个二分类的支持向量机。

理解正则化。在SVM/Softmax的例子中，正则化损失从生物学角度可以看做逐渐遗忘，因为它的效果是让所有突触权重在参数更新过程中逐渐向着0变化。

9. 常用激活函数

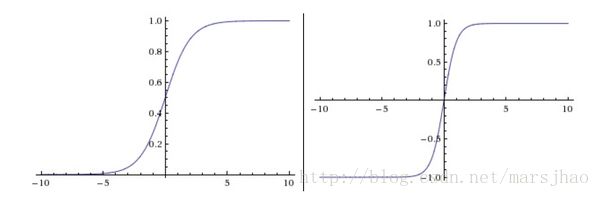
左边是Sigmoid非线性函数，将实数压缩到[0,1]之间。右边是tanh函数，将实数压缩到[-1,1]。

Sigmoid的两个主要缺点：Sigmoid函数饱和使梯度消失；Sigmoid函数的输出不是零中心的。

Tanh：。

左边是ReLU（校正线性单元：Rectified Linear Unit）激活函数，当x = 0时函数值为0。当x>0函数的斜率为1。右边图表指明使用ReLU比tanh收敛快6倍。

ReLU。在近些年ReLU变得非常流行。它的函数公式是。换句话说，这个激活函数就是一个关于0的阈值（如上图左侧）。使用ReLU有以下一些优缺点：

优点1：相较于sigmoid和tanh函数，ReLU对于随机梯度下降的收敛有巨大的加速作用。这是由它的线性，非饱和的公式导致的。

优点2：sigmoid和tanh神经元含有指数运算等耗费计算资源的操作，而ReLU可以简单地通过对一个矩阵进行阈值计算得到。

缺点：在训练的时候，ReLU单元比较脆弱并且可能“死掉”。如果学习率设置得太高，可能会发现网络中40%的神经元都会死掉（在整个训练集中这些神经元都不会被激活）。通过合理设置学习率，这种情况的发生概率会降低。

Leaky ReLU。Leaky ReLU是为解决“ReLU死亡”问题的尝试。

Maxout。Maxout神经元就拥有ReLU单元的所有优点（线性操作和不饱和），而没有它的缺点（死亡的ReLU单元）。然而和ReLU对比，它每个神经元的参数数量增加了一倍，这就导致整体参数的数量激增。

最后需要注意一点：在同一个网络中混合使用不同类型的神经元是非常少见的，虽然没有什么根本性问题来禁止这样做。

一句话：用ReLU非线性函数。注意设置好学习率，或许可以监控你的网络中死亡的神经元占的比例。如果单元死亡问题困扰你，就试试Leaky ReLU或者Maxout，不要再用sigmoid了。也可以试试tanh，但是其效果应该不如ReLU或者Maxout。

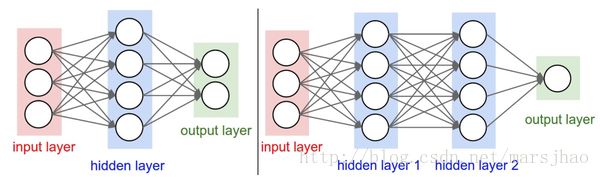
10. 神经网络结构

最普通的层的类型是全连接层（fully-connected layer）。

命名规则。当我们说N层神经网络的时候，我们没有把输入层算入。

前向传播。全连接层的前向传播一般就是先进行一个矩阵乘法，然后加上偏置并运用激活函数。

输出层。和神经网络中其他层不同，输出层的神经元一般是不会有激活函数的（或者也可以认为它们有一个线性相等的激活函数）。

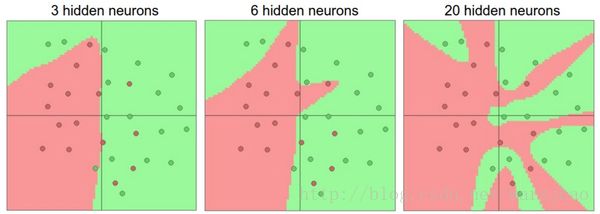
卷积神经网络的情况却不同，在卷积神经网络中，对于一个良好的识别系统来说，深度是一个极端重要的因素。

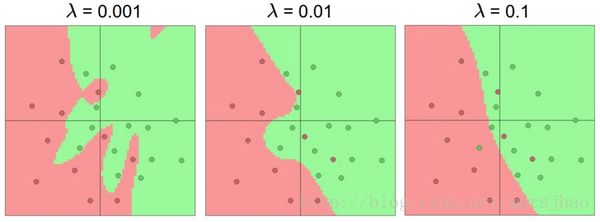
过拟合（Overfitting）是网络对数据中的噪声有很强的拟合能力而没有重视数据间（假设）的潜在基本关系。防止神经网络的过拟合有很多方法（L2正则化，dropout和输入噪音等）。

不应该因为害怕出现过拟合而使用小网络。相反，应该进尽可能使用大网络，然后使用正则化技巧来控制过拟合。