面试题14 I: 剪绳子 (Python36) 动态规划

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

思路1 查表法

如下

class Solution:
    def cuttingRope(self, n: int) -> int:
        res = [0, 0, 1, 2, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 243, 324, 486, 729, 972, 1458, 2187, 2916, 4374, 6561, 8748,13122, 19683, 26244, 39366, 59049, 78732, 118098, 177147, 236196, 354294, 531441, 708588, 1062882, 1594323, 2125764,3188646, 4782969, 6377292, 9565938, 14348907, 19131876, 28697814, 43046721, 57395628, 86093442, 129140163, 172186884,258280326, 387420489, 516560652, 774840978, 1162261467, 1549681956]
        return res[n]

思路2 利用数学知识求解

分绳子时每段长度应尽可能为3，若实在无法为3，可为2。(若长度实在太短无法为2则可为1.)

具体的数学证明见该链接：https://leetcode-cn.com/problems/jian-sheng-zi-lcof/solution/mian-shi-ti-14-i-jian-sheng-zi-tan-xin-si-xiang-by/

直观上也可以理解：

假设最优乘积n1*n2*n3...*na中存在ni=4,则可以将ni拆为(2,2)，积不变。这意味着3和2可以完全替代4，且2比1优先。

同理，假设最优乘积n1*n2*n3...*na中存在ni=5,则可以将ni拆为(2,3)，积2*3=6>5.与n1*n2*n3...*na是最优乘积矛盾。因此，最优乘积中的长度必不可能为5.

再同理，假设最优乘积n1*n2*n3...*na中存在ni=6,则可以将ni拆为(3，3)，积3*3=9>6.与n1*n2*n3...*na是最优乘积矛盾。因此，最优乘积中的长度必不可能为6.

以此类推，不难理解：分绳子时每段长度应尽可能为3，若实在无法为3，可为2。(若长度实在太短无法为2则可为1.)

 

这样，我们就可以有如下代码：

class Solution:
    def cuttingRope(self, n: int) -> int:
        if n <= 3:  # n>1且m>1. 若n=2,则返回1；若n=3则返回2
            return n -1
        mod_type = n % 3    # n>=4。余数只能是0，1，2
        power3 = n // 3
        power2 = 0  
        if mod_type == 1:   # 如果余数为1.则必然能够和一个3组成2*2，故power2=2；同时3的个数减1即可
            power2 = 2
            power3 -= 1
        elif mod_type == 2: # 如果余数为2，则直接为2
            power2 = 1
        # 如果余数为0，则不用改变
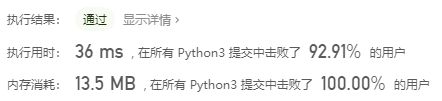
        return int(math.pow(3, power3) * math.pow(2, power2))

这种方法时间复杂度O(1),空间复杂度O(1)，因此效果很好：

 

思路3 动态规划

求解思路：设S[n]表示长度为n时的最大乘积，那么必然有：

S[n] = max{S[n-1], 2*S[n-2], 3*S[n-3], 4*S[n-4],5*S[n-5] ...}

但显然2*S[n-2]>=4*S[n-4]>5*S[n-5]...，因此保留

S[n] = max{S[n-1], 2*S[n-2], 3*S[n-3]} （n>6）即可

 

代码如下：

class Solution:
    def cuttingRope(self, n: int) -> int:
        s = [1]*59   # 定义初始数组
        s[2] = 1
        s[3] = 2
        s[4] = 4
        s[5] = 6
        s[6] = 9
        for i in range(7,59):
            s[i] = max(s[i-1], s[i-3]*3, s[i-2]*2)
        
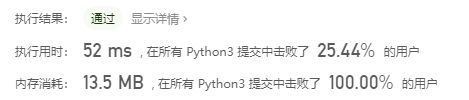
        return s[n]

但这样空间复杂度是O(N)，时间复杂度是O(N),因此会慢很多：

 

总结

Python创建1维list: [1]*length即可