百度机器学习训练营笔记——数学基础

原文博客：Doi技术团队
链接地址：https://blog.doiduoyi.com/authors/1584446358138
初心：记录优秀的Doi技术团队学习经历

均值（mean，average）

• 代表一组数据在分布上的集中趋势和总体上的平均水平。
• 常说的中心化（Zero-Centered）或者零均值化（Mean-subtraction），就是把每个数值都减去均值。

$$\mu =\frac{1}{N}\sum _{i=1}^N{x}_i\left(x:x_1,x_2,...,x_N\right)$$

import numpy as np

# 一维数组
x = np.array([-0.02964322, -0.11363636, 0.39417967, -0.06916996, 0.14260276])
print('数据：', x)

# 求均值
avg = np.mean(x)
print('均值：', avg)

输出：

数据： [-0.02964322 -0.11363636  0.39417967 -0.06916996  0.14260276]
均值： 0.064866578

标准差（Standard Deviation）

• 代表一组数据在分布上第离散程度。
• 方差是标准差的平方。

$$\sigma =\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(x_i-\mu \right)}^2}\left(x:x_1,x_2,...,x_N\right)$$

import numpy as np

# 一维数组
x = np.array([-0.02964322, -0.11363636, 0.39417967, -0.06916996, 0.14260276])
print('数据：', x)

# 求标准差
std = np.std(x)
print('标准差：', std)

输出：

数据： [-0.02964322 -0.11363636  0.39417967 -0.06916996  0.14260276]
标准差： 0.18614576055671836

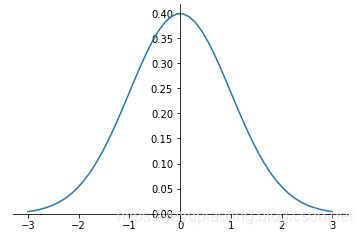
正态分布（Normal Distribution）

• 又叫“常态分布”，“高斯分布”，是最重要的一种分布。
• 均值决定位置，方差决定幅度。
• 表示：$X\sim N\left(\mu ,{\sigma }^2\right)$

正态分布的概率密度函数：
$$f(x)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}$$

import numpy as np
from matplotlib import pyplot as plt

def nd(x, u=-0, d=1):
    return 1/np.sqrt(2*np.pi*d)*np.exp(-(x-u)**2/2/d**2)
    
x = np.linspace(-3, 3, 50)
y = nd(x)
plt.plot(x, y)

# 调整坐标
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.show()

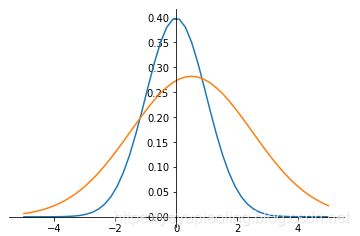
非标准正态分布的标准化（Normalization）

• 将非标准正态变为标准正态。
• 将每个数据减均值，除标准差。

$$y=\frac{x-\mu }{\sigma }$$

import numpy as np
from matplotlib import pyplot as plt

def nd(x, u=0, d=1):
    return 1/np.sqrt(2*np.pi*d)*np.exp(-(x-u)**2/2/d**2)
    
x = np.linspace(-5, 5, 50)
y1 = nd(x)
y2 = nd(x, 0.5, 2)
plt.plot(x, y1)
plt.plot(x, y2)

# 调整坐标
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.show()

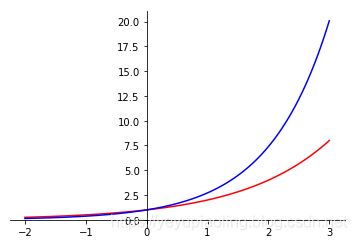
指数函数（Exponent）

• 常用2, e的指数函数；
• 输入为任意实数；
• 输出为非负数。

$$y_1=2^x$$
$$y_2=e^x$$

import numpy as np
from matplotlib import pyplot as plt

x = np.linspace(-2, 3, 100)
y1 = 2**x
y2 = np.exp(x)
plt.plot(x,y1, color='red')
plt.plot(x, y2, color='blue')

# 调整坐标
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.show()

对数函数（Logarithm）

• 常用以2, e, 10为底的对数函数；
• 定义域为正数；
• 值域为全体实数；
• 输入在(0, 1)范围内时，输出为负数。

$$y_1=lo{g}_{2}x$$
$$y_2=lnx$$
$$y_3=lgx$$

import numpy as np
from matplotlib import pyplot as plt

x = np.linspace(0.01, 10, 100)
y1 = np.log2(x)
y2 = np.log(x)
y3 = np.log10(x)
plt.plot(x, y1, color='red')
plt.plot(x, y2, color='blue')
plt.plot(x, y3, color='green')

# 调整坐标
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.show()

Softmax函数

• 在分类网络的输出层中作激活函数，输出概率；
• 先通过指数函数，把所有输出都变为整数；
• 再做归一化，每个数都除以所有数的和，输出各分类的概率。

$$P_i=\frac{e^{x_i}}{{\sum }_{i=1}^N{e}^{x_i}}\left(x:x_1,x_2,\dots ,x_N\right)$$

import numpy as np

x = np.array([-0.02964322, -0.11363636, 0.39417967, -0.06916996, 0.14260276])
print('原始输出：', x)
prob = np.exp(x)/np.sum(np.exp(x))
print('概率输出：', prob)

输出：

原始输出： [-0.02964322 -0.11363636  0.39417967 -0.06916996  0.14260276]
概率输出： [0.17868493 0.16428964 0.27299323 0.17175986 0.21227234]

One-hot 编码

• 在分类网络中，用于对类别进行编码；
• 编码长度等于类别数；
• 每个编码只有一位为1，其余都为0；
• 所有编码向量都正交。

示例：
假如有5类，则编码为：
第一类：[1, 0, 0, 0, 0]
第二类：[0, 1, 0, 0, 0]
第三类：[0, 0, 1, 0, 0]
第四类：[0, 0, 0, 1, 0]
第五类：[0, 0, 0, 0, 1]

交叉熵（Cross Entropy）

• 常用于分类问题中，做损失函数；
• 从分布的角度，让预测概率趋近于标签。

$Label:[l_1,l_2,\dots ,l_N]$ ——经过One-hot编码

$predict:[P_1,P_2,\dots ,P_N]$ ——经过Softmax函数

$$ce=-\sum _{i=1}^N{l}_i\cdot {\log }^{P_i}$$

import numpy as np

# one-hot 编码的标签
label = np.array([0,0,1,0,0])
print('分类标签：', label)
# 网络实际输出
x1 = np.array([-0.02964322, -0.11363636, 3.39417967, -0.06916996, 0.14260276])
x2 = np.array([-0.02964322, -0.11363636, 1.39417967, -0.06916996, 5.14260276])
print('网络输出1:', x1)
print('网络输出2:', x2)
# softmax 之后的模拟概率
p1 = np.exp(x1) / np.sum(np.exp(x1))
p2 = np.exp(x2) / np.sum(np.exp(x2))
print('概率输出1:', p1)
print('概率输出2:', p2)
# 交叉熵
ce1 = -np.sum(label * np.log(p1))
ce2 = -np.sum(label * np.log(p2))
print('交叉熵1:', ce1)
print('交叉熵2:', ce2)

输出：

分类标签： [0 0 1 0 0]
网络输出1: [-0.02964322 -0.11363636  3.39417967 -0.06916996  0.14260276]
网络输出2: [-0.02964322 -0.11363636  1.39417967 -0.06916996  5.14260276]
概率输出1: [0.02877271 0.02645471 0.88293386 0.0276576  0.03418112]
概率输出2: [0.00545423 0.00501482 0.02265122 0.00524284 0.96163688]
交叉熵1: 0.12450498821197674
交叉熵2: 3.787541448750617

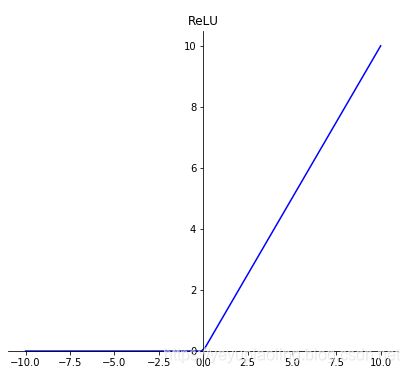
激活函数（Activation Function）

• 引入非线性因素，使模型有更强的表达能力；
• 输出层采用softmax激活，可以模拟输出概率；
• sigmoid和tanh都有饱和区，会导致梯度消失；
• 在深度学习中，sigmoid和tanh主要用于做各种门或开关；
• 在深度学习中，最常用的激活函数为ReLU及其变体。

$$\delta (x)=\frac{1}{1+e^{-x}}$$
$$Tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
$$ReLU(x)=max(x,0)$$

import numpy as np
from matplotlib import pyplot as plt

x = np.linspace(-10, 10, 100)
# plt.figure(31)
plt.figure(figsize=(10, 20))

# Sigmoid
sigmoid = 1 / (1 + np.exp(-x))
top = np.ones(100)
plt.subplot(311)
plt.plot(x, sigmoid, color='blue')
plt.plot(x, top, color='red', linestyle='-.', linewidth=0.5)
plt.title(s='Sigmoid')

# Tanh
tanh = (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
top = np.ones(100)
bottom = -np.ones(100)
plt.subplot(312)
plt.plot(x, tanh, color='blue')
plt.plot(x, top, color='red', linestyle='-.', linewidth=0.5)
plt.plot(x, bottom, color='red', linestyle='-.', linewidth=0.5)
plt.title('Tanh')

# ReLU
relu = np.maximum(x, 0)
plt.subplot(313)
plt.plot(x, relu, color='blue')
plt.title('ReLU')


# 调整坐标
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.show()

源代码地址：https://aistudio.baidu.com/aistudio/projectdetail/176057