中正平和的机器人学笔记——7. 一种气驱型柔性臂的逆运动学模型
1. 前言
上一篇分析了Air-Octor的正运动学模型,这一篇是学习另一篇论文1的笔记,着重分析这种柔性臂的逆运动学模型,也就是通过 k ϕ k_\phi kϕ 和 ϕ \phi ϕ 以及 s s s 来求 l 1 l_1 l1、 l 2 l_2 l2、 l 3 l_3 l3。
2. 逆运动学模型的求解
逆运动学模型的求解大致分为这么几步:先算出 β \beta β,再计算 h c h_c hc,由此计算出 h i h_i hi,得到 h i h_i hi 以后再通过计算就可以得到 l i l_i li
2.1 求解 h c h_c hc
2 π r a = 2 π ϕ \cfrac{2\pi r}{a} = \cfrac{2\pi}{\phi} a2πr=ϕ2π
将上述公式中的 r r r 代换成 1 k ϕ \cfrac{1}{k_\phi} kϕ1, a a a 代换成 s n \cfrac{s}{n} ns, ϕ \phi ϕ 代换成 β \beta β就可以求出 β \beta β:
β = s k ϕ n \beta = \cfrac{sk_\phi}{n} β=nskϕ
有了 β \beta β 的值以后,我们利用如下的三角形求 h c h_c hc:
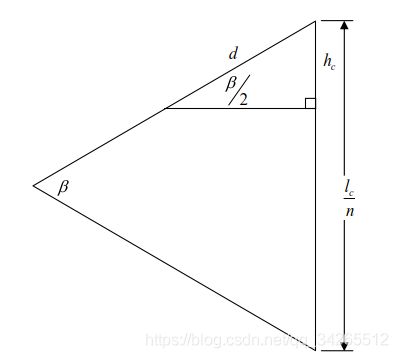
观察上图可得关系式
sin ( β 2 ) = h c d \sin\left(\cfrac{\beta}{2}\right) = \cfrac{h_c}{d} sin(2β)=dhc
整理后可得
h c = d sin ( s k ϕ 2 n ) h_c = d\sin\left(\cfrac{sk_\phi}{2n}\right) hc=dsin(2nskϕ)
3.2 求解 h i h_i hi
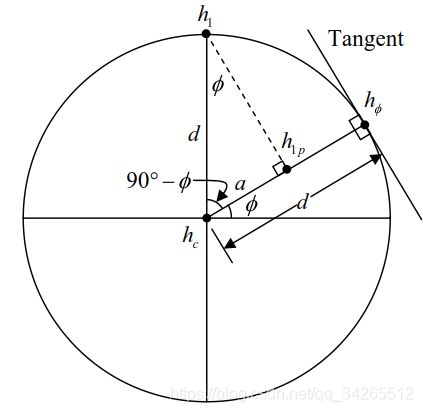
观察下图:
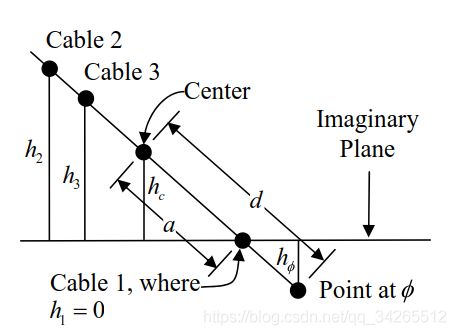
这里要说明,在上一篇,求正运动学模型时,我们是设定 h 1 = 0 h_1 = 0 h1=0 来确定了一个假想的平面,这里我们求解逆运动学模型的时候,稍微改动一下,设定 h ϕ = 0 h_\phi = 0 hϕ=0,虽然上图仍然是 h 1 = 0 h_1 = 0 h1=0 的情况。
通过上图我们可以得到关系式:
h 1 − h ϕ d − a = h c − h ϕ d \cfrac{h_1 - h_\phi}{d - a} = \cfrac{h_c - h_\phi}{d} d−ah1−hϕ=dhc−hϕ
化简上式可以得到 h 1 h_1 h1
h 1 = h c − h ϕ d ( d − a ) + h ϕ h_1 = \cfrac{h_c - h_\phi}{d}(d-a) + h_\phi h1=dhc−hϕ(d−a)+hϕ
cos ( π 2 − ϕ ) = a d = sin ϕ \cos\left(\cfrac{\pi}{2}-\phi\right) = \cfrac{a}{d} = \sin{\phi} cos(2π−ϕ)=da=sinϕ
通过上式我们可以化简之前求得的 h 1 h_1 h1:
h 1 = d sin ( s k ϕ 2 n ) ( 1 − sin ϕ ) h_1 = d\sin\left(\cfrac{sk_\phi}{2n}\right)\left(1 - \sin\phi\right) h1=dsin(2nskϕ)(1−sinϕ)
( h 2 h_2 h2、 h 3 h_3 h3 自己动手求吧哈哈)
3.3 求解 l i l_i li
回忆上一篇的求解过程,我们可以把 l i l_i li 分解成两部分:
l i = l ϕ + 2 n h i l_i = l_\phi + 2nh_i li=lϕ+2nhi
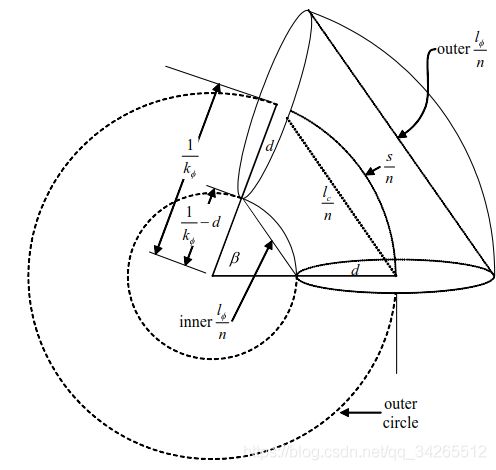
然后 h i h_i hi 我们已经求出来了,接下来就求一下 l ϕ l_\phi lϕ。观察下图

显然,啊,显然可以得到
sin ( β 2 ) = l ϕ 2 n 1 k ϕ − d \sin\left(\cfrac{\beta}{2}\right) = \cfrac{\cfrac{l_\phi}{2n}}{\cfrac{1}{k_\phi} - d} sin(2β)=kϕ1−d2nlϕ
哎那这 l ϕ l_\phi lϕ 就很好求了:
l ϕ = 2 n ( 1 k ϕ − d ) sin ( s k ϕ 2 n ) l_\phi = 2n\left(\cfrac{1}{k_\phi} - d\right)\sin\left(\cfrac{sk_\phi}{2n}\right) lϕ=2n(kϕ1−d)sin(2nskϕ)
整合上面推导的结果,就可以求出 l 1 l_1 l1啦:
l 1 = 2 n sin ( s k ϕ 2 n ) ( 1 k ϕ − d sin ϕ ) l_1 = 2n\sin\left(\cfrac{sk_\phi}{2n}\right)\left(\cfrac{1}{k_\phi} - d\sin\phi\right) l1=2nsin(2nskϕ)(kϕ1−dsinϕ)
同样的,将 ϕ \phi ϕ 旋转 21 0 ο 210^\omicron 210ο 和 33 0 ο 330^\omicron 330ο 就可以得到 l 2 l_2 l2 和 l 3 l_3 l3:
l 2 = 2 n sin ( s k ϕ 2 n ) ( 1 k ϕ + d sin ( π 3 + ϕ ) ) l_2 = 2n\sin\left(\cfrac{sk_\phi}{2n}\right)\left(\cfrac{1}{k_\phi} + d\sin\left(\cfrac{\pi}{3} + \phi\right)\right) l2=2nsin(2nskϕ)(kϕ1+dsin(3π+ϕ))
l 3 = 2 n sin ( s k ϕ 2 n ) ( 1 k ϕ − d sin ( π 6 + ϕ ) ) l_3 = 2n\sin\left(\cfrac{sk_\phi}{2n}\right)\left(\cfrac{1}{k_\phi} - d\sin\left(\cfrac{\pi}{6} + \phi\right)\right) l3=2nsin(2nskϕ)(kϕ1−dsin(6π+ϕ))
这里注意到,借助等价无穷小 lim x → 0 sin x = x \lim\limits_{x \to 0}{\sin x = x} x→0limsinx=x, 我们可以得到
lim k ϕ → 0 l 1 = 2 n sin ( s k ϕ 2 n ) ( 1 k ϕ − d sin ϕ ) = 2 n ( s k ϕ 2 n ) ( 1 k ϕ − d sin ϕ ) = s \lim\limits_{k_\phi \to 0}{l_1 = 2n\sin\left(\cfrac{sk_\phi}{2n}\right)\left(\cfrac{1}{k_\phi} - d\sin\phi\right)} = 2n\left(\cfrac{sk_\phi}{2n}\right)\left(\cfrac{1}{k_\phi} - d\sin\phi\right) =s kϕ→0liml1=2nsin(2nskϕ)(kϕ1−dsinϕ)=2n(2nskϕ)(kϕ1−dsinϕ)=s
同样可得 lim k ϕ → 0 l 2 = lim k ϕ → 0 l 3 = s \lim\limits_{k_\phi \to 0}l_2 = \lim\limits_{k_\phi \to 0}l_3 = s kϕ→0liml2=kϕ→0liml3=s
也就是说当曲率趋向于0(延展变平不弯曲)的情况下,我们求得的逆运动学模型 l i l_i li 会趋向于 s s s,而这也符合实际情况,说明我们求得的模型是正确的。
3.4 归纳整理
l 1 = 2 n sin ( s k ϕ 2 n ) ( 1 k ϕ − d sin ϕ ) l_1 = 2n\sin\left(\cfrac{sk_\phi}{2n}\right)\left(\cfrac{1}{k_\phi} - d\sin\phi\right) l1=2nsin(2nskϕ)(kϕ1−dsinϕ)
l 2 = 2 n sin ( s k ϕ 2 n ) ( 1 k ϕ + d sin ( π 3 + ϕ ) ) l_2 = 2n\sin\left(\cfrac{sk_\phi}{2n}\right)\left(\cfrac{1}{k_\phi} + d\sin\left(\cfrac{\pi}{3} + \phi\right)\right) l2=2nsin(2nskϕ)(kϕ1+dsin(3π+ϕ))
l 3 = 2 n sin ( s k ϕ 2 n ) ( 1 k ϕ − d sin ( π 6 + ϕ ) ) l_3 = 2n\sin\left(\cfrac{sk_\phi}{2n}\right)\left(\cfrac{1}{k_\phi} - d\sin\left(\cfrac{\pi}{6} + \phi\right)\right) l3=2nsin(2nskϕ)(kϕ1−dsin(6π+ϕ))
以上就是我们推导得到的逆运动学模型,仍然,用到的数学工具很简单。
4. 总结
本周的两篇博客主要写了Air-Octor柔性臂的正逆运动学模型的推导,这是论文中很关键的部分,但不是全部,主要是学习人家这种分析的思路和角度,这才是最重要的,因为也可以看到,跟着人家的思路跑,无非是温习了一下高中几何而已,这样看论文收获不会太到。看完一篇论文,如何真正消化吸收其精髓,坦白讲,我只是个新得不能再新的萌新,也在不断学习。
W. McMahan, B. Jones, I.D. Walker, V. Chitrakaran, A. Seshadri, and D. Dawson, '“Robotic Manipulators Inspired by Cephalopod Limbs” link:https://www.researchgate.net/publication/228997554_Robotic_manipulators_inspired_by_cephalopod_limbs ↩︎