强化学习（二）- 动态规划（Dynamic Programming）

3.动态规划

3.1 介绍

术语动态规划(DP：Dynamic Programming) 指的是一个算法集合，可以用来计算最优策略，给定一个完美的环境模型，作为马尔可夫决策过程(MDP)。经典的DP算法在强化学习中的应用有限，因为它们的假设是一个完美的模型，而且计算量大，但它们仍然具有重要的理论意义。DP为理解其余部分中介绍的方法提供了必要的基础。实际上，所有这些方法都可以被看作是实现与DP几乎相同的效果的尝试，只不过计算量更少，而且没有假设一个完美的环境模型。

我们通常假设环境是一个有限的MDP。也就是说，我们假设它的状态、行为和奖励集$\mathcal{S}$、$\mathcal{A}$和$\mathcal{R}$是有限的，并且它的动力是由一组概率$p(s^{\prime },r|s,a)$对于所有$s\in \mathcal{S},a\in \mathcal{A}(s),r\in \mathcal{R}$和$s^{\prime }\in {\mathcal{S}}^{+}$(${\mathcal{S}}^{+}$是$\mathcal{S}$在情节性任务中加上最终态)给出的。尽管DP思想可以应用于具有连续状态和动作空间的问题，但是精确解只有在特殊情况下才有可能。对于具有连续状态和动作的任务，获取近似解的一种常用方法是将状态和动作空间量化，然后应用有限状态DP方法。

DP的关键思想，以及一般的强化学习，是使用价值函数来组织和结构寻找好的策略。在动态规划部分将展示如何使用DP来计算之前定义的价值函数。一旦我们找到满足Bellman最优性方程的最优价值函数$v_{\ast }$或$q_{\ast }$，我们就可以很容易地获得最优策略
$$\begin{array}{rl}{v}_{\ast }(s)& =\underset{a}{\max }\mathbb{E}[R_{t+1}+\gamma v_{\ast }(S_{t+1})|S_t=s,A_t=a]\\ & =\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\ast }(s^{\prime })]\end{array}\text{\hspace{1em}(3.1)}$$
$$\begin{array}{rl}{q}_{\ast }(s,a)& =\mathbb{E}[R_{t+1}+\gamma \underset{a^{\prime }}{\max }{q}_{\ast }(S_{t+1},a^{\prime })|S_t=s,A_t=a]\\ & =\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \underset{a^{\prime }}{\max }{q}_{\ast }(s^{\prime },a^{\prime })]\end{array}\text{\hspace{1em}(3.2)}$$
以上公式适用于$s\in \mathcal{S},a\in \mathcal{A}(s),s^{\prime }\in {\mathcal{S}}^{+}$。DP算法是通过将Bellman方程转化为赋值，也就是说，转化为改进期望价值函数的近似的更新规则来获得的。

3.2 策略评估(预测)

首先考虑如何计算任意策略$\pi$的状态价值函数$v_{\pi }$。这在DP文献中称为策略评估（policy evaluation）。我们也称之为预测问题(predition problem)。对于所有$s\in \mathcal{S}$
$$\begin{array}{rl}{v}_{\pi }(s)& \doteq {\mathbb{E}}_{\pi }[G_t|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s]\\ & =\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]\end{array}\text{\hspace{1em}(3.3)}$$

其中$\pi (a|s)$是在策略$\pi$下，在$s$状态下采取行动$a$的概率，期望以$\pi$为下标来表示它们以$\pi$为条件。$v_{\pi }$的存在和独特性由$0<\gamma <1$保证或者所有状态的最终终止由策略$\pi$决定。

如果环境动力是完全已知的，则(3.3)是一个含$|\mathcal{S}|$未知数的$|\mathcal{S}|$线性方程组原则上，它的解是一个直接的但繁琐的计算。迭代求解方法是最合适于我们的目的的。考虑一个近似价值函数序列v0, v1, v2，…，每个${\mathcal{S}}^{+}$映射到$\mathbb{R}$(实数)。初始近似v0是任意选择的(除了终点状态必须赋值为0之外)，每次逐次近似都使用$v_{\pi }$的Bellman方程作为更新规则
$$\begin{array}{rl}{v}_{k+1}(s)& \doteq {\mathbb{E}}_{\pi }[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s]\\ & =\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]\text{ for all }s\in \mathcal{S}\end{array}\text{\hspace{1em}(3.4)}$$
明显的是，$v_k=v_{\pi }$是更新规则的固定点，因为$v_{\pi }$的Bellman方程保证了在这种情况下其是相等的。确实，序列$\{v_k\}$可以被证明当$k\to \infty$并且在$v_{\pi }$存在的相同条件下一般收敛于$v_{\pi }$。该算法称为迭代策略评估（iterative policy evaluation）。

为了从$v_k$中产生每一个连续的近似值$v_{k+1}$，迭代策略评估对每一个状态$s$应用了同样的操作：它沿着被评估的策略下所有可能的单步转换，用一个从$s$的后续状态的旧值和预期的即时回报中得到的新值来替换$s$的旧值。我们称这种操作为预期更新（expected update）。迭代策略评估的每一次迭代都会更新一次每个状态的值，以产生新的近似价值函数$v_{k+1}$。有几种不同的预期更新，取决于更新的是一个状态（如这里）还是一个状态动作对，以及取决于后续状态的估计值的精确组合方式。在DP算法中完成的所有更新都被称为预期更新，因为它们是基于对所有可能的下一个状态的预期，而不是基于一个样本下一个状态。

要编写一个顺序计算机程序来实现由(3.4)给出的迭代策略评估，就必须使用两个数组，一个是旧值$v_k(s)$，一个是新值$v_{k+1}(s)$。使用两个数组，新值可以从旧值中逐一计算出来，而不改变旧值。当然，使用一个数组，使用更新值替代，也就是每个新值立即覆盖旧值，这样更方便。那么，根据状态更新的顺序，有时会用新值代替(3.4）右侧的旧值。这种就地算法也会收敛到$v_{\pi }$；事实上，正如所期望的那样，它通常比双数组版本收敛得更快，因为它能较为快速的使用新的数据。我们认为更新是在 扫描（sweep） 状态空间时进行的。对于替代算法（in-place algorithm），在扫描过程中，状态值更新的顺序对收敛速度有很大影响。我们在考虑DP算法时，通常会选择替代算法。

在下面的伪代码中显示了迭代策略评估的完整就地版本。注意它是如何处理终止的。在形式上，迭代策略评估只在极限内收敛，但在实践中必须在此之前停止。伪代码在每次扫描后测试数量${\max }_{s\in \mathcal{S}}|v_{k+1}(s)-v_k(s)|$，当数量足够小时停止。

---

迭代策略评估，用于估计$V\approx v_{\pi }$

输入$\pi$,是待评估的策略。
算法参数：对于$s\in {\mathcal{S}}^{+}$,有一个小的阈值$\theta >0$确定估算精度初始化,除了$V(terminal)=0$
伪代码如下：
$$\begin{array}{rl}& \text{Loop:}\\ & \Delta \leftarrow 0\\ & \text{Loop for each s}\in \mathcal{S}:\\ & v\leftarrow V(s)\\ & V(s)\leftarrow \sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V(s^{\prime })]\\ & \Delta \leftarrow max(\Delta ,|v-V(s)|)\\ & \text{until }\Delta <0\end{array}$$

---

例 3.1

下图是一张4x4的网格

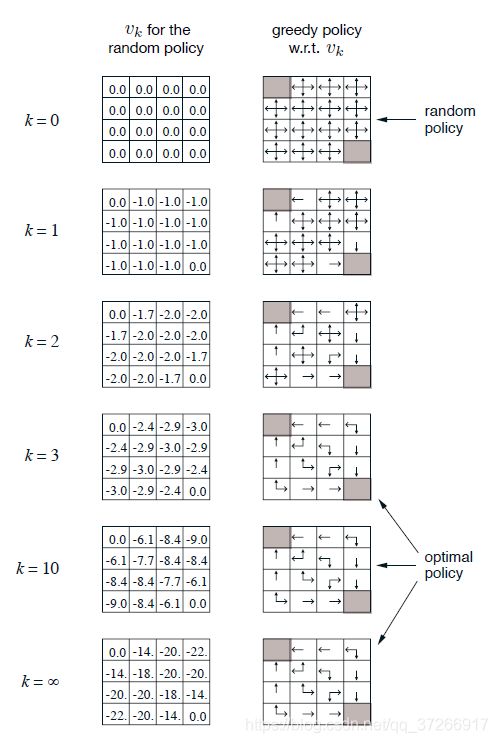
非终点状态是$\mathcal{S}=\{1,2,...,14\}$。在每一个状态中有四个可能的动作，$\mathcal{A}=\{up,down,right,left\}$，它会引起智能体相应的状态的转变，除了将智能体移动出网格（如在1位置，智能体选择向上移动），它只会使智能体的状态保持不变。因此，例如，对于所有$r\in \mathcal{R}$有$p(6,-1|5,right)=1,p(7,-1|7,right)=1$和$p(10,r|5,right)=0$。这是一个无折扣的情节性任务。在到达终点状态之前，所有转换的奖励都是1。终端状态在图中显示为阴影(尽管它显示在两个位置，但它实际上是一个状态)。因此，对于所有状态$s$、$s^{\prime }$和行动$a$，预期回报函数$r(s,a,s^{\prime })=1$。假设智能体遵循等可能随机策略(所有行动都等可能性)。下图左侧为迭代策略评估计算的价值函数$v_k$序列。最终估计实际上是$v$，在这种情况下，它给出了每个状态从该状态到终止的预期步数的否定。

这是这个网格世界上迭代策略评估的收敛性。左列是随机策略的状态价值函数的近似值序列(所有动作都是等可能的)。右列是与价值函数估计值相对应的贪婪策略序列(箭头表示达到最大值的所有动作，显示的数字四舍五入到两个有效数字)。最后一个策略只保证是对随机策略的改进，但在这种情况下，它和第三次迭代后的所有策略都是最优的。

3.3 策略改进（Policy Improvement）

我们计算策略价值函数的原因是为了帮助找到更好的策略。假设我们已经确定了一个任意确定性策略$\pi$的价值函数$v_{\pi }$。对于某些状态，我们想知道我们是否应该改变策略，以确定地选择一个$a\ne \pi (s)$的行动。我们知道从状态$s$开始实行$v_{\pi }(s)$的策略的收益，但是改变成为新策略是好还是坏呢?回答这个问题的一种方法是考虑在状态$s$中选择动作$a$，然后遵循现有的策略$\pi$。这种行为方式的价值是
$$\begin{array}{rl}{q}_{\ast }(s,a)& \doteq \mathbb{E}[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s,A_t=a]\\ & =\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]\end{array}\text{\hspace{1em}(3.5)}$$

关键的标准是这个标准是大于还是小于$v_{\pi }(s)$。如果大于，也就是说，如果在$s$中选择了一次$a$，结果此后的$\pi$比接下来的所有$\pi$都要好，那么人们就会期望每次遇到$s$时选择$a$仍会更好，而且新的策略实际上总体上会更好。

这是一个称为策略改进定理（policy improvement theorem） 的一般结果的特殊情况。假设$\pi$和${\pi }^{\prime }$是任意的，对于$s\in \mathcal{S}$的一对确定性策略。
$$q_{\pi }(s,{\pi }^{\prime }(s))\ge v_{\pi }(s)\text{\hspace{1em}(3.6)}$$
然后策略${\pi }^{\prime }$必须和$\pi$同样或者比它更好。这就是说，对于所有的$s\in \mathcal{S}$，策略${\pi }^{\prime }$必须获得一个更好或者相等的预期回报。
$$v_{{\pi }^{\prime }}(s)\ge v_{\pi }(s)\text{\hspace{1em}(3.7)}$$

此外，如果在任意状态下存在(3.6)的严格不等式，则该状态下必然存在(3.7)的严格不等式。这个结果尤其适用于这两个策略,我们认为在之前规定的,最初确定的策略$\pi$,以及改进的策略,${\pi }^{\prime }$,除了${\pi }^{\prime }(s)=a\ne \pi (s)$。显然，(3.6)适用于除$s$之外的所有状态。因此,如果$q_{\pi }(s,a)>v_{\pi }(s)$，那么更改后的策略确实比之前的策略要好。

策略改进定理证明的背后的思想很容易理解。从(3.6)开始，一直把$q_{\pi }$边展开为(3.5)再加上(3.6)直到我们得到$v_{{\pi }^{\prime }}(s)$:

到目前为止，我们已经看到，给定一个策略及其价值函数，我们可以轻松地评估一个特定动作在单一状态下的策略变化。 这是一种考虑策略改变在所有位置和所有可能的行动的拓展,最好根据$q_{\pi }(s,a)$选择在每个位置的行动。换句话说,考虑新的贪婪策略,
$$\begin{array}{rl}{\pi }^{\prime }(s)& =\underset{a}{\mathrm{argmax}}{q}_{\pi }(s,a)\\ & =\underset{a}{\mathrm{argmax}}\mathbb{E}[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s,A_t=a]\\ & =\underset{a}{\mathrm{argmax}}\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]\end{array}\text{\hspace{1em}(3.8)}$$
其中$\underset{a}{\mathrm{argmax}}$定义为获得后面式子最大值的a的值。根据策略$v_{\pi }$，贪婪策略采取了短期内看起来最好的行动，因为它是在移动一步之后。通过构造，贪心策略满足策略改进定理(3.6)的条件，因此我们知道它和原策略一样好，甚至比原策略更好。通过使新的策略而使原有策略的价值函数变得贪婪，从而改进原有策略的新策略制定过程称为策略改进（policy improvement）。

假设新的贪婪策略${\pi }^{\prime }$和旧的策略相同（不好于旧的策略）。若$v_{\pi }=v_{{\pi }^{\prime }}$，通过（3.8）式我们可以得出对于所有$s\in \mathcal{S}$
$$\begin{array}{rl}{v}_{{\pi }^{\prime }}(s)& =\underset{a}{\max }\mathbb{E}[R_{t+1}+\gamma v_{{\pi }^{\prime }}(S_{t+1})|S_t=s,A_t=a]\\ & =\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{{\pi }^{\prime }}(s^{\prime })]\end{array}$$
但这和Bellman最优性方程(3.1)是一样的，因此$v_{{\pi }^{\prime }}$一定是$v_{\ast }$, $\pi$和${\pi }^{\prime }$一定都是最优策略。
因此，策略改进必须给我们一个严格意义上更好的策略，除非原来的策略已经是最优的。

到目前为止我们已经考虑了确定性策略的特殊情况。在一般情况下，一个随机策略$\pi$指定了在每个状态 $s$ 中采取每个行动 $a$ 的概率 $\pi (a|s)$。我们将不再赘述，但事实上本节的所有思想都很容易扩展到随机策略。特别是，策略改进定理在随机情况下的应用。此外，如果在策略改进步骤中存在联系，如(3.8).也就是说，如果有几个动作在其中达到最大值.那么在随机情况下，我们不需要从其中选择一个动作。相反，每个最大化的行动可以被赋予新的贪婪策略中被选择的一部分概率。只要所有的次最大行动被赋予零概率，任意分配方案都是允许的。

之前的图中最后一行显示了一个随机策略改进的例子。这里原策略$\pi$是等概率随机策略，新策略${\pi }^{\prime }$是是策略$\pi$的贪婪策略。左下图为价值函数$v_{\pi }$，右下图为可能的${\pi }^{\prime }$集合。${\pi }^{\prime }$图中带有多个箭头的状态是指几个行动达到(3.8)中最大值的状态；允许在这些行动之间进行任意的概率的分配。任意这样的策略的价值函数$v_{{\pi }^{\prime }}(s)$，在所有状态$s\in \mathcal{S}$下,都是$-1$、$-2$或$-3$，而$v_{\pi }(s)$最多是-14。因此，对于$v_{{\pi }^{\prime }}(s)\ge v_{\pi }(s)$，对于所有$s\in \mathcal{S}$，说明了策略的改进。虽然在这种情况下，新的策略${\pi }^{\prime }$恰好是最优的，但在一般情况下，只能保证改进。

3.4 策略迭代(Policy Iteration)

一旦一个策略$\pi$通过$v_{\pi }$得到改进产生一个更好的策略${\pi }^{\prime }$，我们可以计算${\pi }^{\prime }$并再次改进它产生一个更好的${\pi }^{\prime \prime }$。从而得到一系列单调改进的策略和价值函数:
$${\pi }_{0}E{v}_{{\pi }_0}I{\pi }_{1}E{v}_{{\pi }_1}I{\pi }_{2}E...I{\pi }_{\ast }E{v}_{\ast }$$
其中$E$定义为策略评估，$I$定义为策略改进。每个策略都保证是对前一个策略的严格改进(除非它已经是最优的)。由于一个有限的MDP只有有限数量的策略，这个过程必须在有限次迭代中收敛到一个最优策略和最优价值函数。
这种寻找最佳策略的方法称为策略迭代（Policy Iteration）。完整的算法如下框所示。请注意，每个策略评估本身是一个迭代计算，从前一个策略的价值函数开始。这通常会导致策略评估的收敛速度大大提高(大概是因为从一个策略到下一个策略的价值函数变化很小)。

---

策略迭代(使用迭代策略评估)进行估计$\pi \approx {\pi }_{\ast }$

---

3.5 价值迭代（Value Iteration）

策略迭代的一个缺点是，它的每次迭代都涉及策略评估，而策略评估本身可能是一个旷日持久的迭代计算，需要对状态集进行多次扫描。如果策略评估是迭代进行的，那么只有在极限情况下才会精确收敛到$v_{\pi }$。我们必须等待精确收敛，或者我们可以停止在那之前。例子3.1中的图示例显然表明，截断策略评估是可能的。在该示例中，策略评估迭代超过前三个迭代，对相应的贪婪策略没有影响。

实际上，策略迭代的策略评估步骤可以以多种方式截断，而不会失去策略迭代的收敛保证。一个重要的特殊情况是在一次扫描(每个状态的一次更新)后停止策略评估。这种算法称为价值迭代。可以将其编写为一个特别简单的更新操作，该操作结合了策略改进和截断的策略评估步骤:
$$\begin{array}{rl}{v}_{k+1}(s)& \doteq \underset{a}{\max }\mathbb{E}[R_{t+1}+\gamma v_k(S_{t+1})|S_t=s,A_t=a]\\ & =\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })]\end{array}\text{\hspace{1em}(3.9)}$$

对于任意$v_0$，在保证$v_{\ast }$存在的相同条件下，序列$v_k$可收敛于$v_{\ast }$。

另一种理解值迭代的方法是参考Bellman最优性方程(3.1)。注意，只需将Bellman最优性方程转化为更新规则即可获得价值迭代。还请注意，除了它要求在所有操作中采取最大值之外，价值迭代更新与策略评估更新(3.4)是如何相同的。

最后，我们需要考虑价值迭代是如何终止的。与策略评估一样，价值迭代形式上需要无限次迭代才能精确收敛到$v_{\ast }$。在实践中，一旦价值函数在一次扫描中仅发生少量变化，我们就使程序停止。下面的框显示了具有这种终止条件的完整算法。

---

价值迭代(使用迭代策略评估)进行估计$\pi \approx {\pi }_{\ast }$

---

价值迭代有效地将策略评估和策略改进结合在一起。通过在每次策略改进扫描之间插入多个策略评估扫描，通常可以实现更快的收敛。一般来说，整个被截断的策略迭代算法可以被认为是一组扫描序列，其中一些使用策略评估更新，而另一些使用价值迭代更新。因为(3.9)中的max操作是这些更新之间的唯一区别，这仅仅意味着max操作被添加到策略评估的一些扫描中。所有这些算法都收敛于折现有限MDPs的最优策略。

4.6 异步动态规划（Asynchronous Dynamic Programming）

到目前为止，我们所讨论的DP方法的一个主要缺点是，它们涉及到对MDP的整个状态集的操作，也就是说，它们需要对状态集进行扫描。如果状态集非常大，那么即使是单次扫描也会非常花费时间。例如，西洋双陆棋游戏有超过1020个状态。即使我们可以每秒对100万个状态进行值迭代更新，也需要超过一千年才能完成一次扫频。

异步DP算法是就地迭代的DP算法，它不是以系统性地扫描状态集的方式组织的。这些算法以任意顺序，并且使用其他状态的任意值更新状态的值。一些状态的值可能会在其他状态的值更新一次之前更新几次。然而，为了正确地收敛，异步算法必须继续更新所有状态的值：它不能在计算的某一点之后忽略任意状态。异步DP算法在选择要更新的状态方面有很大的灵活性。

例如，异步价值迭代的一个版本使用值迭代更新(4.10)，在每一步$k$上只更新一个状态$s_k$的值。如果$0\le \gamma \le 1$，只有在所有状态在序列$\{s_k\}$中出现无限次的情况下，才能保证对$v_{\ast }$的渐进收敛（序列甚至可以是随机的）。(在不适用折扣的偶发情况下，有可能存在一些更新的顺序不会导致收敛，但要避免这些是相对容易的)。同样，也可以将策略评估和价值迭代更新混合起来，产生一种异步截断的策略迭代。虽然这种和其他算法相比不寻常的DP算法的细节不在我们的讨论范围，但很明显，一些不同的更新形成了构件，可以灵活地用于各种各样的无扫除DP算法中。

当然，避免扫描并不一定意味着我们可以减少计算量。它只是意味着，一个算法在改善策略方面取得进展之前，不需要被锁定在任意无望的长时间扫描中。我们可以尝试通过选择应用更新的状态来利用这种灵活性，从而提高算法的进步速度。我们可以尝试对更新进行排序，让值信息以有效的方式从一个状态传播到另一个状态。有些状态可能不需要像其他状态那样频繁地更新其值。如果一些状态与最优行为无关，我们甚至可以尝试完全跳过更新它们。

异步算法也使计算与实时交互的混合变得更容易。为了解决一个给定的MDP，我们可以在代理实际经历MDP的同时运行一个迭代DP算法。同时，DP算法的最新值和策略信息可以指导智能体的决策。例如，我们可以在代理访问状态时对状态应用更新。这使得DP算法的更新可以集中到状态集中与代理最相关的部分。这种聚焦是强化学习中反复出现的主题。

4.７ 广义策略迭代（Generalized Policy Iteration）

策略迭代由两个同时进行、相互作用的过程组成，一个使价值函数与当前策略一致(策略评估)，另一个使策略使当前价值函数使用贪婪策略(策略改进)。在策略迭代中，这两个流程交替进行，每个流程在另一个流程开始之前完成，但这实际上并不是必须的。例如，在价值迭代中，在每次策略改进之间只执行一次策略评估迭代。在异步DP方法中，评估和改进过程交错在一个更细的颗粒上。在某些情况下，在返回到另一个进程之前，单个状态会在一个进程中进行更新。只要两个过程继续更新所有状态，最终结果通常是相同的收敛到最优价值函数和最优策略。

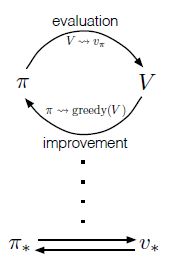
我们使用术语广义策略迭代(generalized policy iteration，GPI) 来表示让策略评估和策略改进过程相互作用、独立于两个过程的颗粒和其他细节的一般思想。几乎所有的强化学习方法都被很好地描述为GPI。也就是说，它们都具有可识别的策略和价值函数，策略总是相对于价值函数进行改进，而价值函数总是被驱动向策略的价值函数，如图所示。如果评价过程和改进过程都稳定下来，即不再产生变化，那么价值函数和策略必须是最优的。价值函数只有在与现行策略一致时才能稳定，而策略只有在对现行价值函数贪婪时才能稳定。因此，只有当一个策略被发现对它自己的评估函数是贪婪的时，两个进程才稳定下来。这意味着Bellman最优性方程(4.1)成立，因此策略和价值函数是最优的。

GPI的评价和改进过程可以看作是竞争和合作的过程。它们相互竞争的意义是它们向相反的方向拉扯。使策略对价值函数贪婪通常会使价值函数对已更改的策略不正确，而使价值函数与策略一致通常会使策略不再是贪婪的。然而，从长远来看，这两个过程相互作用以找到一个联合的解决方案:最优价值函数和最优策略。

人们也可以将GPI中评估和改进过程之间的相互作用考虑为两个约束或目标，例如，在二维空间中的两条线，如图所示。虽然实际的几何比这复杂得多，但图表显示了实际情况。每个流程将价值函数或策略驱动到表示两个目标之一的解决方案的线中的一条。这两个目标相互作用，因为这两条线不是正交的。直接朝着一个目标前进会导致一些偏离另一个目标的运动。然而，联合过程不可避免地更接近最优的总体目标。图中的箭头对应于策略迭代的行为，每个箭头都引导系统完全实现两个目标中的一个。在GPI中，人们还可以朝着每个目标采取更小的、不完整的步骤。在任意一种情况下，这两个过程一起实现了最优的总体目标，即使没有人试图直接实现它。

4.8 动态规划的效率

DP对于非常大的问题可能不实用，但与其他解决MDPs的方法相比，DP方法实际上是相当高效的。如果我们忽略一些技术细节，那么(最坏的情况)DP方法寻找最优策略的时间是状态和行动的多项式。如果n和k表示状态和动作的数量，这意味着DP方法需要的计算操作数量小于n和k的某个多项式函数。即使确定性策略的总数量是$k^n$, DP方法也能保证在多项式时间内找到最优策略。从这个意义上说，DP比策略空间中的任意直接搜索都要快得多，因为直接搜索必须彻底检查每个策略，以提供相同的保证。线性规划方法也可用于求解线性规划问题，在某些情况下，其最坏情况收敛保证优于线性规划方法。但是，与DP方法相比，线性规划方法在更少的状态数量下变得不切实际(约为100倍)。对于最大的问题，只有DP方法是可行的。

DP有时被认为是有限的适用性，因为维数的限制，事实上，状态的数量经常与状态变量的数量呈指数增长。大的状态集确实会产生很大的困难，但这些是问题的固有困难，而不是DP作为一种解决方法的固有困难。事实上，与直接搜索和线性规划等竞争方法相比，DP更适合处理大的状态空间。在实践中，DP方法可以与今天的计算机一起用于求解具有数百万种状态的MDPs。策略迭代和价值迭代都被广泛使用，如果有的话，通常哪一个更好还不清楚。

在实践中，这些方法的收敛速度通常比它们的理论最坏情况运行时间快得多，特别是当它们以良好的初值函数或策略开始时。对于大状态空间的问题，异步DP方法通常是首选。即使要完成同步方法的一次扫描，也需要每个状态的计算和内存。

对于某些问题，即使大内存和计算量也是不切实际的，但是这个问题仍然是潜在的可解决的，因为沿着最优解轨迹出现的状态相对较少。在这种情况下，可以应用异步方法和其他GPI变体，并且可以比同步方法更快地找到好的或最优策略。

4.9 总结

在本章中，我们熟悉了动态规划的基本思想和算法，因为它们与求解有限的MDPs有关。策略评估是指(通常)对给定策略的价值函数进行迭代计算。策略改进是指在给定策略的价值函数的情况下对改进策略的计算。将这两种计算结合在一起，我们获得了策略迭代和价值迭代，这是两种最流行的DP方法。这些都可以用来可靠地计算最优策略和有限MDPs的价值函数给定的MDP的完整知识。

经典的DP方法对状态集进行扫描，对每个状态执行预期的更新操作。每个这样的操作都基于所有可能继承状态的值及其发生概率更新一个状态的值。预期的更新与Bellman方程密切相关:它们只不过是将这些方程转换成赋值语句。当更新不再引起值的变化时，满足相应Bellman方程的值就收敛了。正如有四个主要的价值函数（$v_{\pi },v_{\ast },q_{\pi },q_{\ast }$）。有四个对应的Bellman方程和四个对应的期望更新。DP更新操作的直观视图由它们的备份图提供。

深入了解DP方法，事实上，几乎所有的强化学习方法，可以通过将它们视为广义策略迭代(GPI)来获得。GPI是围绕一个近似策略和一个近似价值函数的两个相互作用过程的一般思想。一个流程接受给定的策略并执行某种形式的策略评估，将价值函数更改为更接近策略的真实价值函数。另一个过程是将价值函数作为给定的，进行某种形式的策略改进，改变策略使之更好，假设价值函数就是策略的价值函数。尽管每个流程都改变了另一个流程的基础，但总的来说，它们一起工作以找到一个共同的解决方案:策略和价值函数对任意一个流程都是不变的，因此是最优的。在某些情况下，GPI可以被证明是收敛的，特别是对于经典的DP方法。在其他情况下，收敛性没有被证明，但GPI的想法仍然提高了我们对方法的理解。

没有必要对状态集执行DP方法的完全扫描。异步DP方法是就地迭代方法，它以任意顺序更新状态，可能是随机确定的，并使用过时的信息。许多这些方法可以看作是GPI的细粒度形式。