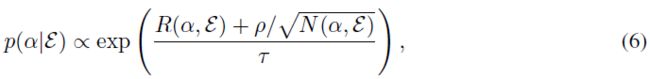Discovering Reinforcement Learning Algorithms

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

 arXiv:2007.08794v1 [cs.LG] 17 Jul 2020

 

Abstract

　　强化学习（RL）算法根据经过多年研究手动发现的几种可能规则之一来更新智能体的参数。从数据中自动发现更新规则可能会导致效率更高的算法，或者更适合特定环境的算法。尽管已经进行了尝试来应对这一重大的科学挑战，但是仍然存在一个未决的问题，即发现RL基本概念的替代方法（例如价值函数和时序差分学习）是否可行。本文介绍了一种新的元学习方法，该方法通过与一组环境交互来发现整个更新规则，其中包括“预测什么”（例如价值函数）和“如何从中学习”（例如bootstrapping）。此方法的输出是RL算法，我们称为学习型策略梯度（LPG）。实证结果表明，我们的方法发现了它自己的替代价值函数的概念。此外，它发现了一种bootstrapping机制来维持和使用其预测。出乎意料的是，仅在toy环境中进行训练时，LPG可以有效地推广到复杂的Atari游戏中，并达到非凡的性能。这表明从数据中发现通用RL算法的潜力。

 

1 Introduction

　　强化学习（RL）有一个明确的目标：最大化期望累积奖励（或平均奖励），这很简单，但又足以捕获智能的许多方面。即使RL的目标很简单，但开发有效的算法来优化该目标通常需要大量的研究工作，从建立理论到实证研究。一种有吸引力的替代方法是从与一组环境交互生成的数据中自动发现RL算法，这可以表述为元学习问题。最近的工作表明，当给定价值函数时，可以元学习策略更新规则，并且生成的更新规则可以推广到相似的或没见过的任务（参见表1）。
　　但是，完全从头开始发现RL的基本概念是否可行仍然是一个悬而未决的问题。特别地，RL算法的定义方面是它们学习和利用价值函数的能力。发现价值函数之类的概念需要同时理解“预测什么”和“如何利用预测”。从数据中发现这尤其具有挑战性，因为在多次更新过程中，预测仅对策略具有间接影响。我们假设一种能够发现自身价值函数的方法可能还会发现其他有用的概念，从而有可能为RL开辟全新的方法。

　　基于上述开放性问题，本文朝着发现通用RL算法迈出了一步。我们引入了一个元学习框架，该框架从与环境分布交互产生的数据中共同发现“智能体应该预测什么”和“如何使用预测来改进策略”。我们的架构，即学习型策略梯度（LPG），不会对智能体的矢量值输出强制执行任何语义，而是允许更新规则（即元学习器）决定此矢量应预测的内容。然后，我们提出一个元学习框架，以从多个学习智能体发现这种更新规则，每个学习智能体都与不同的环境进行交互。

　　实验结果表明，我们的算法可以发现有用的函数，并有效地使用这些函数来更新智能体策略。此外，经验分析表明，发现的函数趋向于对价值函数的概念进行编码，并且还通过bootstrapping的形式来维护该价值函数。我们还评估了发现的RL算法推广到新环境的能力。令人惊讶的是，即使仅从与很小的一组toy环境的交互中发现了更新规则，也能够将其推广到许多复杂的Atari游戏[2]，如图9所示。首先要证明有可能发现整个更新规则，并且从toy域中发现的更新规则可以与具有挑战性的基准人工设计算法竞争。

 

2 Related Work

EarlyWork on Learning to Learn 关于学会学习的想法已经讨论了很长时间，包括改进基因编程[26]，学习神经网络更新规则[3]，学习率适应[29]，自权重修改RNN[27]，以及域不变知识的迁移[31]。这些工作表明，不仅可以学习优化固定目标，而且可以改进在元级别进行优化的方式。

 

Learning to Learn for Few-Shot Task Adaptation 学会学习在few-shot学习的背景下受到了很多关注[25,33]。MAML[9,10]允许通过反向传播参数更新来元学习初始参数。RL²[7,34]通过在智能体的整个生命周期中展开LSTM[14]，将学习本身描述为RL问题。其他方法包括简单逼近[23]，具有Hebbian学习的RNN[19,20]和梯度预处理[11]。所有这些在智能体和算法之间都没有明确区分，因此根据问题的定义，生成的元学习算法特定于单个智能体结构。

 

Learning to Learn for Single Task Online Adaptation 不同的工作集重点在于学会在单个生命周期内学习单个任务。Xu et al.[37]引入了元梯度RL方法；它使用智能体的更新进行反向传播，以计算相对于更新的元参数的梯度。该方法已应用于元学习各种形式的算法组件，例如折扣因子[37]，内在奖励[40]，辅助任务[32]，回报[35]，辅助策略更新[41]，非策略更正[38]，和更新目标[36]。相反，我们的工作有一个正交的目标：发现对更广泛的智能体和环境有效的通用算法，而不是适应特定的环境。

 

Discovering Reinforcement Learning Algorithms 已经进行了一些尝试，以从与环境分布的交互中学习通用算法（请参见表1进行比较）。EPG[15]使用进化策略来找到策略更新规则。Zheng et al.[39]表明，可以通过奖励函数的形式对用于探索的通用知识进行元学习。ML³[5]使用元梯度对损失函数进行元学习。但是，现有技术仅限于特定领域的算法，因为它们只能将相同领域内的相似任务进行归纳。最近，MetaGenRL[17]被提出来元学习域不变的策略更新规则，该规则可以从几个MuJoCo环境推广到其他MuJoCo环境。但是，没有先前的工作试图发现完整的更新规则。取而代之的是，它们全都依赖于价值函数（可以说是RL的最基本构建块）进行bootstrapping。相比之下，我们的LPG元学习bootstrapping机制。此外，本文是第一个表明从toy环境到具有挑战性的基准的彻底归纳是可能的。

 

3 Meta-Learning Framework for Learned Policy Gradient

　　所提出的元学习框架的目标是从环境p(ε)和初始智能体参数p(θ₀)的分布中找到由η参数化的最优更新规则：

其中是生命周期结束时的期望回报。直观地，该目标旨在找到一个更新规则η，以便在将其用于更新智能体的参数直到其生命周期结束（θ₀ → … → θ_N）时，智能体会在给定的环境中最大化期望回报。产生的更新规则称为学习型策略梯度（LPG）。图1和算法1总结了元训练过程的概述。

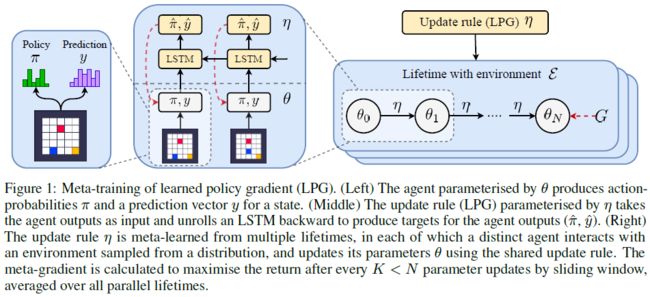
图1：学习型策略梯度（LPG）的元训练。（左侧）通过θ参数化的智能体产生状态的动作概率π和预测向量y。（中部）通过η参数化的更新规则（LPG）将智能体输出作为输入，并反向展开LSTM以生成智能体输出（）的目标。（右侧）更新规则是从多个生命周期元学习的，在每个生命周期中，不同的智能体与从分布中采样的环境进行交互，并使用共享的更新规则更新其参数。在所有K

 

3.1 LPG Architecture 

　　如图1所示，LPG是由元参数η参数化的更新规则，它要求智能体产生策略π_θ(a|s)和m维分类预测向量y_θ(s) ∈ [0, 1]^m。LPG是一个反向的LSTM[14]网络，它产生如何根据智能体的轨迹来更新策略和预测矢量作为输出。更具体地说，它需要在每个时间步骤t处采取下式：

其中r_t是奖励，d_t是指示episode终止的二值，并且γ是折扣因子。通过构造，LPG不会将观察空间和动作空间作为输入，因此它不会改变。取而代之的是，它仅采用所选动作的概率π(a|s)。这种结构允许LPG架构应用于完全不同的环境，同时防止过拟合。

 

3.2 Agent Update (θ)

　　通过在以下方向执行梯度上升来更新智能体参数：

其中是LPG的输出。是Kullback-Leibler散度。α_y是用于预测更新的系数。在较高的层次上，指定应如何调整动作概率，并直接影响智能体的行为。指定智能体应针对给定状态预测的目标类别分布，并且在LPG发现有用的语义（例如，价值函数）并使用y通过bootstrapping间接更改策略之前，不会对策略产生影响，这使发现问题具有挑战性。

　　注意，所提出的框架不限于智能体更新和架构的这种特定形式（例如，具有KL散度的分类预测）。我们探索这种特定形式的部分原因是分布RL[1,6]的成功。但是，我们不对y强制执行任何语义，但允许LPG从数据中发现y的语义。

 

3.3 LPG Update (η)

　　对LPG进行元训练时，要考虑到它可以在多大程度上改进与不同类型环境交互的智能体群的性能。具体而言，通过将策略梯度应用于等式1中的目标来计算元梯度，具体如下：

　　直观地，我们使用从θ₀到θ_N的更新规则η执行N次参数更新，直到生命周期结束为止，并估计更新参数θ_N的策略梯度，以找到使θ_N的期望回报（G）最大化的元梯度方向。这需要通过智能体的更新过程进行反向传播，如[37,10]中所述。实际上，由于内存限制，我们考虑使用较小的滑动窗口，并在每K

 

Regularisation 我们发现优化可能非常困难且不稳定，这主要是因为LPG需要学习预测的适当语义，以及学习正确地使用预测y进行bootstrapping而不需要访问价值函数。为了稳定训练，我们建议在目标上添加以下正则化，从而得出元梯度：

其中H(·)是熵，而{β_i}是每个正则化项的元超参数。H(y)不利于确定性预测，这与策略熵正则化H(π)具有相同的动机[21]。这些不适用于智能体，但适用于更新规则，因此生成的LPG具有此类属性。的L2正则化防止更新过于激进。我们将在第4.4节中讨论这些正则化的效果。

 

3.4 Balancing Agent Hyperparameters for Stabilisation (α)

　　虽然先前的方法[5,17]在元训练期间使用固定智能体超参数（例如，学习率），但在跨完全不同的环境进行元训练时，我们发现这是有问题的。例如，如果用于环境A的学习率恰好大于用于环境B的学习率，则的最优尺度对于A而言应较小，对于B而言应较大。由于更新规则与环境无关，因此它将会产生在两个环境之间矛盾的元梯度，从而使元训练变得不稳定。此外，由于它们对η的依赖关系，不可能对超参数进行预平衡，这在元训练期间会发生变化，从而导致平衡超参数内在不稳定的问题。为了解决这个问题，我们修改了等式1中的目标：

其中α = {α_lr, α_y}是一个学习率和一个预测更新系数（请参见等式2）。该目标在给定每个环境最优超参数的情况下寻求最优更新规则。为了优化这一点，在实践中，我们提出使用赌博机p(α|ε)对每个生命周期采样超参数，并根据每个生命周期结束时的回报更新采样分布。通过使p(α|ε)适应每种环境，超参数可在整个环境之间自动平衡，这使得元梯度的噪声较小。请注意，这仅在元训练期间完成。在没见过的环境中进行元测试期间，需要以与现有RL算法相同的方式手动选择超参数。补充材料中描述了有关如何在我们的实验中完成此操作的更多详细信息。

 

4 Experiment

　　实验旨在回答以下研究问题：

• LPG能否发现有效的bootstrapping预测的有用语义？
• 发现的预测语义是什么？
• 发现预测语义有多重要？
• 正则化和超参数的平衡有多重要？
• LPG可以从toy环境推广到复杂的Atari游戏吗？

 

4.1 Experimental Setup

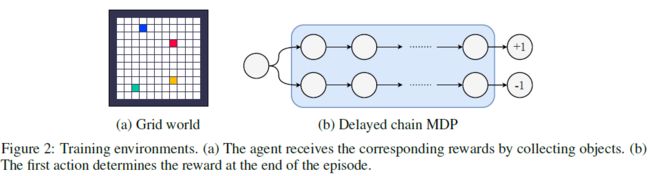
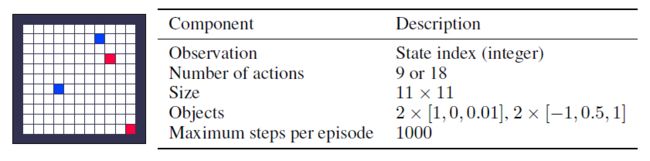
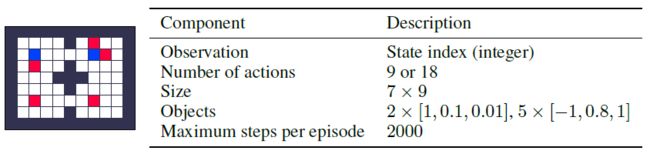
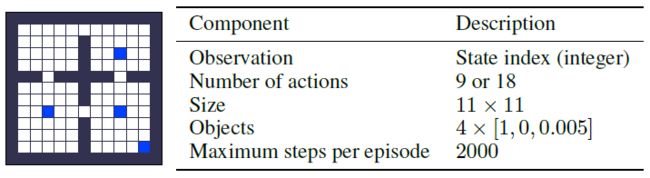
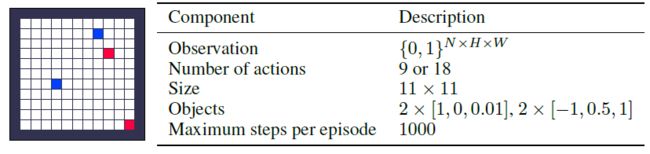
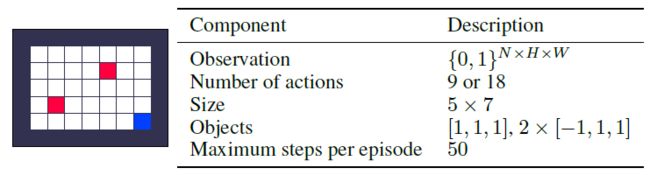
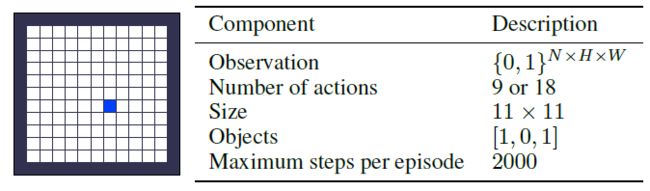
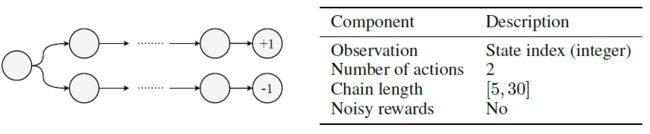
Training Environments 对于LPG的元训练，我们引入了三种不同的toy域，如图2所示。表格式网格世界是具有固定对象位置的网格世界。随机网格世界对每个eposide都有随机的对象位置。延迟链MDP是具有延迟奖励的简单MDP。每个域有5种不同的环境，具有不同数量的奖励状态和episode长度。训练环境旨在捕获基本的RL挑战，例如延迟奖励，带噪奖励和长期责任分配。大多数训练环境都是表格式的，没有涉及任何函数逼近。补充材料中描述了所有环境的详细信息。

 

Implementation Details 我们使用了30维预测向量y ∈ [0, 1]³⁰。在元训练期间，我们每20个时间步骤更新一次智能体参数。由于大多数训练episode跨越20-2000个步骤，因此LPG必须为预测y发现长期语义，以便能够最大化来自部分轨迹的长期未来回报。该算法使用JAX[4]实现。补充材料中描述了更多的实现细节。

 

Baselines 如第2节和表1所述，除MetaGenRL[17]外，大多数先前的工作不支持在完全不同的环境中进行归纳。但是，MetaGenRL设计用于连续控制并且基于DDPG[28,18]。相反，为了调查发现预测语义的重要性，我们将其与自己的基准LPG-V（LPG的变体）进行比较，该变体与MetaGenRL一样，仅在给定由TD(λ)[30]训练的价值函数的情况下才学习策略更新规则（）（没有发现它自身的预测语义）¹。此外，我们还将优势执行者-评论者（A2C）[21]作为人类发现的标准算法基准进行了比较。

 

¹LPG-V不能完全代表MetaGenRL，因为它包含了本文介绍的其他改进。

 

4.2 Specialising in Training Environments

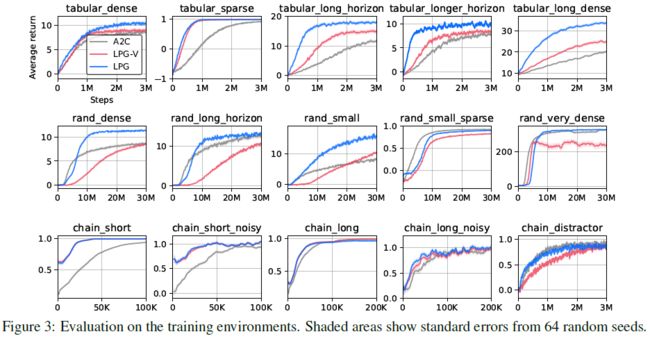
　　我们在训练环境中评估了LPG，以查看LPG是否已发现有效的更新规则。图3中的结果表明，在大多数训练环境中，LPG的性能均优于A2C。这表明所提出的框架可以发现更新规则，该规则优于给定环境下用于发现的外部算法（即等式4中的策略梯度）。此外，结果表明LPG专门研究某些类别的环境，并且如果有人对一类特定的RL问题感兴趣，那么LPG可能是比手工设计的RL算法更好的解决方案。另一方面，LPG-V比LPG差很多，但显然不比A2C好。这表明发现预测语义是性能的关键，这与以前的工作相反，前一个工作仅学习策略更新规则，而后者依赖真实价值函数（请参见表1），这证明了我们的方法是正确的。

 

4.3 Analysis of Learned Policy Gradient

What does the prediction (y) look like? 由于发现的预测语义是性能的关键，因此一个自然的问题是发现的概念是什么以及它们如何工作。为了回答这个问题，我们首先在给定的表格式网格世界实例和固定策略上对预测进行可视化，如图4所示。具体地说，我们在固定策略参数的同时使用LPG仅更新了y，这类似于策略评估。² 图4c中的可视化显示，某些预测在正奖励状态附近具有较大的值，并且类似于图4b中的真实值，它们传播到附近的状态。该可视化内容隐式表明LPG正在要求智能体预测未来的奖励并将此类信息用于bootstrapping。

 

²为避免过拟合，我们创建了一个未见过的网格世界任务，其中包含一个未见过的动作空间。

 

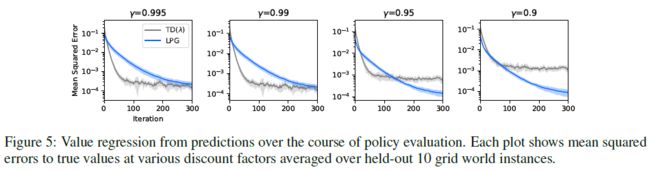
Does the prediction (y) capture true values and beyond? 为了进一步研究预测的丰富程度，我们为许多网格世界实例生成了如图4c所示的y向量，折现因子为0.995，并训练了价值回归模型，这是一个1层的多层感知器（MLP），用于仅根据对0.995到0.9的各种折扣因子的预测y来预测真实价值。然后，我们评估了在保留的一组网格世界上价值回归的精度。为了进行比较，用TD(λ)从折扣因子0.995的价值到其他折扣因子的价值，我们还训练了一个价值回归模型。

　　有趣的是，图5中的结果表明，在LPG更新的原始折扣因子（0.995）下，从y的价值回归几乎与TD(λ)一样好，这意味着y中的信息足够丰富，可以恢复价值函数的原始概念。更有趣的是，图5还显示了y以较低的折扣因子捕获了真实价值，即使它是用0.995的折扣因子生成的。另一方面，标量值中带有TD(λ)的信息太局限了，无法捕获较低折扣因子的价值。该结果表明，提出的框架可以自动发现丰富而有用的预测语义，即使在元训练期间未强制执行这种语义，该预测语义也几乎可以恢复各种视野下的价值函数。

 

Does the prediction (y) converge? 通过不同的RL方法获得的预测的收敛性是其最关键的特性之一。诸如时序差分（TD）学习之类的经典算法对表格式设置中的精确定义的语义（即期望回报）具有收敛保证[30]。另一方面，LPG没有这样的保证，因为预测语义是元学习的，其唯一目的是提高智能体的性能，这意味着LPG原则上可以包含非收敛的动态系统，该系统可以循环或发散。因此，我们实证研究了LPG的收敛性。图6中的结果表明，当由LPG更新时，两个不同的预测向量（y₀，y₁）收敛到几乎相同的值。这意味着，即使没有任何理论约束，从所提出的框架中自然会出现预测收敛的平稳语义。

 

4.4 Ablation Study

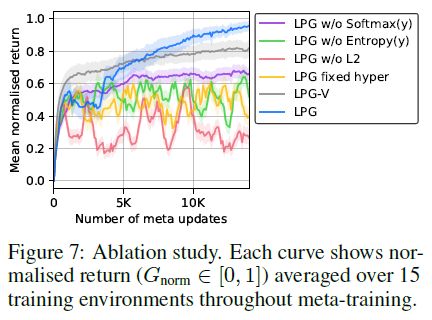
　　如第3.2节所述，我们发现元训练非常困难且不稳定，因为发现整个更新规则是必需的。图7总结了本文介绍的每个想法的效果。'LPG w/o Softmax(y)' 使用y ∈ R³⁰，不带softmax，但使用等式2中的KL散度代替。'LPG w/o Entropy(y)' 和 'LPG w/o L2' 分别没有y的熵正则化和等式4中的L2正则化。'LPG fixed hyper' 是针对每种训练环境使用固定的超参数进行训练的，而不是像第3.4节中介绍的那样在元训练期间平衡它们。图7的结果表明，所有这些想法对于性能都是至关重要的，并且在没有任何一个的情况下训练往往非常不稳定。另一方面，我们发现即使没有正则化工具，LPG-V的元训练也是稳定的。但是，LPG-V收敛到局部最优更新规则，而LPG最终通过发现预测内容找到了更好的更新规则。该结果支持了我们的假设，即尽管优化可能会更加困难，但发现价值函数的替代方案更有可能找到更好的更新规则。

 

4.5 Generalising from Toy Environments to Atari Games

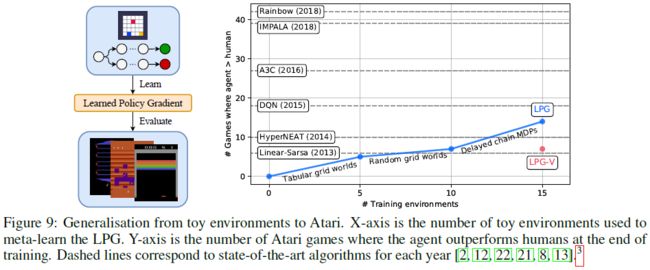
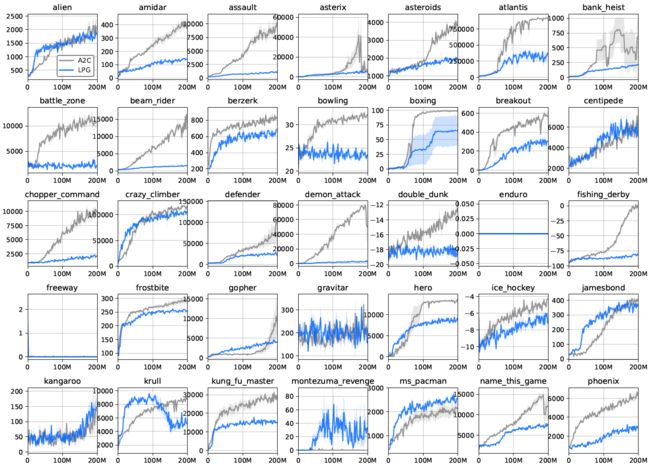
　　要了解仅在toy环境中发现普通LPG的情况，我们直接在复杂的Atari游戏中对LPG进行了评估。如图9所示，与高级RL算法相比，LPG可以很好地推广到Atari游戏。令人惊讶的是，训练环境主要由表格式的环境组成，其基本任务比Atari游戏要简单得多，而且LPG在元训练期间从未见过如此复杂的领域。不过，接受LPG训练的智能体可以在许多Atari游戏中学习复杂的行为，从而在14款游戏中实现超越人类的智能体，而无需依赖任何手工设计的RL组件（例如价值函数），而是使用从头开始发现的自己的更新规则。
　　我们发现特定类型的训练环境（例如延迟链MDP）显著提高了泛化性能（请参见图9）。这表明可能存在一个小型但经过精心设计的环境，这些环境捕获了RL中的重要挑战，因此，当用于元训练时，生成的LPG具有足够的通用性，可以在许多复杂域中良好地运行。

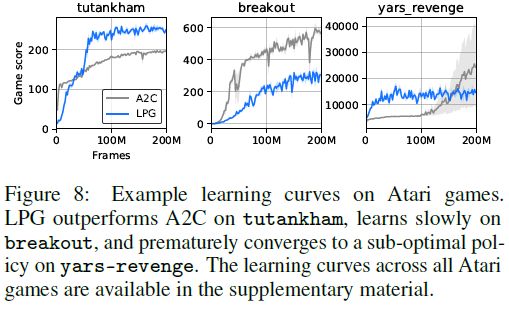
　　尽管LPG仍然落后于诸如A2C之类的高级RL算法，但LPG不仅在训练环境上而且在一些Atari游戏中也胜过A2C（例如，参见图8），这表明LPG专门研究特定类型的RL问题，而不是严格比A2C差。另一方面，图9显示，随着训练环境数量的增加，泛化性能快速提高，这表明，一旦有更多的环境可用于元训练，发现通用的RL算法可能是可行的。

 

³该图用于与人类发现的算法并行显示LPG的进程，由于不同的预处理和函数逼近，因此不能严格比较算法。

 

5 Conclusion

　　本文首次尝试通过结合发现“预测什么”和“如何进行bootstrap”来元学习完整的RL更新规则，从而取代了现有的RL概念（例如价值函数和TD学习）。一小组toy环境的结果表明，发现的LPG可以在预测中保留丰富的信息，这对于有效的bootstrapping至关重要。我们认为，这只是完全数据驱动的RL算法发现的开始；从程序生成环境到新的高级结构以及替代的产生经验的方法，有许多很有希望的方向来扩展我们的工作。从toy域到Atari游戏的激进归纳表明，从与环境的交互中发现有效的RL算法是可行的，这有可能导致全新的RL方法。

 

Broader Impact

　　通过以数据驱动的方式使发现过程自动化，所提出的方法具有极大地加速发现新的强化学习（RL）算法的过程的潜力。如果所提出的研究方向成功，这可能会将研究范式从人工开发RL算法转变为构建适当的环境集，从而使所得算法高效。
　　此外，提出的方法还可以用作协助RL研究人员开发和改进其手工设计算法的工具。在这种情况下，所提出的方法可用于根据研究人员提供的输入结构，提供关于良好更新规则的外观的见解，从而可以加快RL算法的手动发现。
　　另一方面，由于所提出方法的数据驱动性质，所得算法可能会捕获环境训练集中的意外偏差。在我们的工作中，除了发现算法时的奖励，我们没有提供特定领域的信息，这使得算法很难在训练环境中捕获偏差。但是，需要更多的工作来消除发现的算法中的偏差，以防止潜在的负面结果。

 

A Training Environments

A.1 Tabular Grid World

　　当智能体收集对象时，它会收到相应的奖励r，并且episode以与该对象相关联的概率ε_term终止。收集时该对象消失，并在每个时间步骤以概率ε_respawn重新出现。在以下各节中，我们将每个对象类型 i 描述为，其中N是类型 i 的对象数量。

 

Observation Space 在表格式网格世界中，对象位置在生命周期间是随机的，但在一个生命周期内是固定的。因此，在每个生命周期中只有p x 2^m个可能状态，其中p是可能位置的数量，m是对象总数。一个智能体简单地由一个表来表示，该表具有每个状态的不同π(a|s)和y(s)值，而没有任何函数近似。

 

Action Space 有两个不同的动作空间。一种版本包括9个在相邻位置的移动动作（包括停留在同一位置）和9个在相邻位置收集对象的动作。其他版本只有9个动作。在此版本中，当智能体访问对象时会自动收集该对象。我们在元训练期间针对每个生命周期随机采样一个动作空间。

 

A.1.1 Dense

 

A.1.2 Sparse

 

A.1.3 Long Horizon

 

A.1.4 Longer Horizon

 

A.1.5 Long Dense

 

A.2 Random Grid World

　　随机网格世界与表格式网格世界几乎相同，除了对象位置在一个生命周期中是随机的。更具体地，在每个episode的开始随机确定对象位置，并且在收集对象之后将对象重新出现在随机位置。由于随机性，状态空间呈指数增长，这需要函数逼近来表示智能体。观测值由张量{0, 1}^{N x H x W}组成，其中N是对象类型的数量，H x W是网格的大小。

 

A.2.1 Dense

 

A.2.2 Long Horizon

 

A.2.3 Small

 

A.2.4 Small Sparse

 

A.2.5 Very Dense

 

A.3 Delayed Chain MDP

　　此环境的灵感来自Behavior Suite[24]中的Umbrella环境。智能体对每个时间步骤都有一个二值选择（a₀，a₁）。第一个动作决定episode结束时的奖励（1或-1）。该episode在固定数量的步骤（即链长）后终止，该链长是针对每个生命周期从预定义范围内随机采样并在一个生命周期内是固定的。对于每个episode，我们随机决定哪个动作会带来正奖励，并采样相应的链MDP。因为所有状态都是不同的，所以没有状态混叠。可选地，对于中间与智能体的动作无关的状态，可能会有带噪的奖励{1, -1}。

 

A.3.1 Short

 

A.3.2 Short and Noisy

 

A.3.3 Long

 

A.3.4 Long and Noisy

 

A.3.5 State Distraction

　　在这个延迟链MDP中，观察值s_t ∈ {0, 1}²²由两个相关比特组成：a₀是否是正确的动作以及智能体是否选择了正确的动作，以及带噪的比特{0, 1}²⁰，这在所有状态下随机独立采样。智能体被要求去查找相关比特，而忽略观察中的带噪比特。

 

B Implementation Details

B.1 Meta-Training

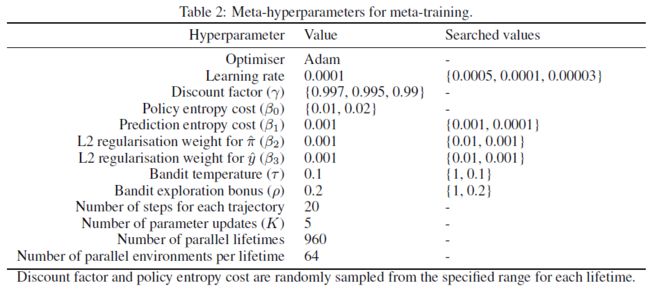
　　我们通过模拟960个并行生命周期（即元梯度的批大小）来训练LPG，每个生命周期都有一个学习智能体与一个采样环境进行交互，总共进行了约10¹⁰个交互步骤。在每个生命周期中，智能体使用从64个并行环境生成的一批轨迹（即智能体的批大小）更新其参数。每个轨迹包括20个步骤。因此，每个参数更新包括64 x 20个步骤。表2总结了用于元训练的元超参数。

 

Details of LPG Architecture 在每个时间步骤t处，LPG网络取，其中r_t是奖励，d_t是指示episode终止的二值，并且γ是折扣因子。使用共享嵌入网络(φ): Dense(16)-Dense(1)将y_θ(s_t)和y_θ(s_{t + 1})映射到标量。具有256个单元的反向LSTM需要作为输入，并生成作为输出。我们对LSTM核心进行了少许修改，以便将隐含状态重置为终止状态（d_t = 0），这将阻止信息流经各个episode。在我们的初步实验中，这通过使LPG难以利用特定于环境的模式来提高了泛化性能。在整个实验过程中，将ReLU用作激活函数。

 

Details of LPG Update 在第3.3节中，为简化起见，将用于更新LPG的元梯度描述为REINFORCE的结果。然而，在实践中，我们使用了优势执行者-评论者（A2C）[21]来计算元梯度，这需要自学习的学习价值函数。请注意，仅对价值函数进行了训练以减少元梯度的方差。LPG本身在元训练和元测试期间无法使用价值函数。原则上，用于发现的外部算法可以是任何RL算法，只要它们被设计为最大化累积奖励即可。

 

Details of Hyperparameter Balancing 如第3.4节所述，我们训练了一个赌博机p(α|ε)以针对每个环境自动采样更好的智能体超参数，以使元训练更加稳定。 更具体地说，赌博机根据以下条件在每个生命周期的开始对超参数进行采样：

其中R(α, ε)是在智能体生命周期结束时具有环境ε中超参数的最终回报，该回报是过去10个生命周期的平均价值。N(α, ε)是模拟的生命周期数。τ是温度常数，ρ是探索奖励的系数。直观地，我们跟踪每个α的性能并采样超参数，这些超参数往往会产生更大的最终回报，并带来探索奖励。在我们的实验中，α由两个超参数组成：用于更新智能体预测的学习率（α_lr）和KL成本（α_y）。表3显示了赌博机搜索的超参数范围。请注意，这种超参数平衡需要经历多次，这只能在元训练期间完成。在未见过的环境上进行元测试期间，α需要手动选择。

 

Preventing Early Divergence 我们发现，元训练可能不稳定，尤其是在训练初期，这是因为随机初始化的更新规则（η）倾向于使智能体发散或确定性，最终导致爆炸性的元梯度。为了解决此问题，只要策略的熵变为0，即表示策略具有确定性，我们就会重置生命周期。我们观察到，这是在训练的早期几次触发的，但随着更新规则的改进，最终不会在训练的后期触发。

 

B.2 Meta-Testing

　　我们根据两款Atari游戏（breakout，boxing）的验证性能选择了最优更新规则（η）和超参数，并使用它们来评估所有57种Atari游戏。我们发现减去基准会稍微改进Atari游戏的性能，如下所示：

其中，f_θ(s)是与动作无关的基准函数。表4中汇总了超参数，图10中显示了学习曲线。

 

B.3 Computing Infrastructure

　　我们的实现基于使用TPU[16]的JAX[4]。训练环境也用JAX实现，它也可以在TPU上运行。使用16核TPU-v2大约需要24小时进行收敛。

 

C Generalisation to Atari Games