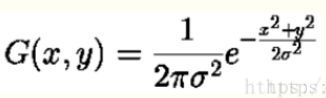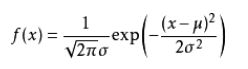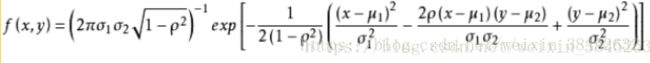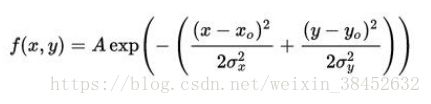初识 OpenCV 之高斯滤波
高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。
通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。
了解高斯滤波之前，我们首先熟悉一下高斯噪声。高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。
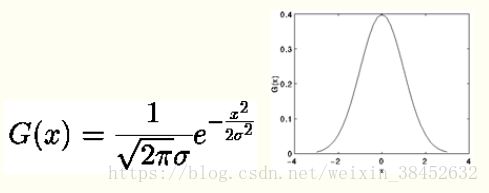
一维高斯：是不是感觉很熟悉，这就是我们高中学的。。。。。。
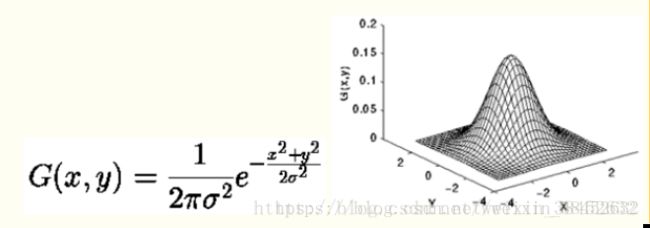
二维高斯：
高斯滤波的具体操作是：
用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
其实滤波是掩膜和图像的卷积，那么求出掩膜才是重点，既然是高斯滤波，那么掩膜肯定跟这条公式
有关联的，下面我们来分析一下这条公式，为什么不用第一条呢？因为一维，掩膜是二维的
这个系数是可以被忽略掉的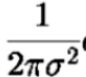
，很简单就是因为它是一个常数，最后也要归一化。
归一化，在数据给定的前提下，令常数 ，常数 ，那么归一化的新的形式就是
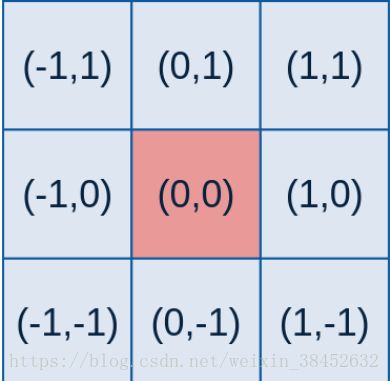
那么剩下的就是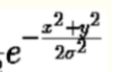
根模板有关系那就是x^2+y^2了，也就是他们就是模板的坐标点，中心点是原点
一维正态分布：
还记得高中学的正态分布的u正好就是中点
二维正态分布：
这里的u1和u2大概就是中心点吧，哈哈哈哈啊哈哈我猜的，我觉得下面的图这条公式更好理解，也是（x0，y0）
通过高斯分布公式计算出需要使用的高斯核（GaussKern），也就是计算出各个位置的所需的权重大小，使得不同位置的像素值影响度不同，距离中心点的越远的位置，权重越小，反之越近的权重越大。
这也是上面为什么讲到这是一种加权平均的过程。。。。。。
参考这个大哥的:https://www.cnblogs.com/wangguchangqing/p/6407717.html
那么模板是怎么求出来的，也就是f（x）的值，确定一个sigma
void generateGaussianTemplate(double window[][11], int ksize, double sigma)
{
static const double pi = 3.1415926;
int center = ksize / 2; // 模板的中心位置，也就是坐标的原点
double x2, y2; f
or (int i = 0; i < ksize; i++)
{
x2 = pow(i - center, 2);
for (int j = 0; j < ksize; j++)
{
y2 = pow(j - center, 2);
double g = exp(-(x2 + y2) / (2 * sigma * sigma));
g /= 2 * pi * sigma;
window[i][j] = g;
}
}
double k = 1 / window[0][0]; // 将左上角的系数归一化为1
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
window[i][j] *= k;
}
}
}
这样计算出来的模板有两种形式：小数和整数。
1 小数形式的模板，就是直接计算得到的值，没有经过任何的处理；
2 整数形式的，则需要进行归一化处理，将模板左上角的值归一化为1