用matlab实现机械臂正逆运动学控制
设计要求:
1.建立一个三自由度的机器人
2.建立坐标系,给出 D-H 参数表;
3.推导正运动学,并写出机器人的齐次变换矩阵;
4.推导逆运动学,并让机器人完成按要求绘制给定图形。
5.MATLAB 程序源代码;
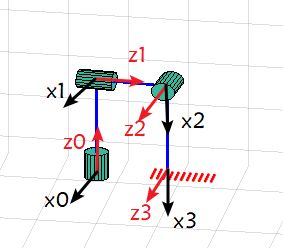
一、 设计三轴机器人
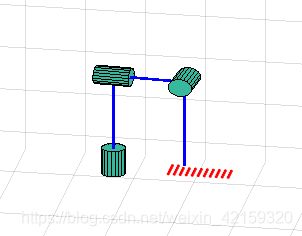
设计出如上图的三轴机器人,第一个和第三个轴是旋转的,第二个是伸长的。第一个轴到第二个轴的距离是100cm,第二个轴的伸长量是0~100cm,第三个轴到手持器的距离是100cm。因此可以得出D-H参数表。
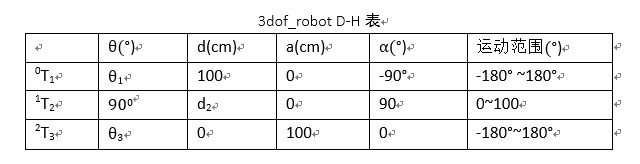
二、 建立坐标系,给出 D-H 参数表
建立坐标系如下所示,由下图得出下面的D-H参数表
三、 推导正运动学,并写出三个齐次变换矩阵
假设现在位于本地参考坐标系xn-zn,那么通过以下4步标准运动即可到达下一个本地参考坐标系xn+1-zn+1。
- 绕z_n轴旋转θ_(n+1),使得x_n 和x_(n+1)互相平行;
- 沿z_n 轴平移d_(n+1) 距离,使得x_n 和x_(n+1) 共线;
- 沿已经旋转过的x_n轴平移a_(n+1)的距离,使得x_n 和x_(n+1)的原点重合;
- 将z_n轴绕x_(n+1)轴旋转α_(n+1),使得z_n轴与z_(n+1)轴对准;
根据矩阵右乘可得到以下结果

根据3dof_robot D-H表表以及上面公式,可得机器人的正运动学方程如下


四、 推导逆运动学,并让机器人完成按要求绘制给定图形


U1与A3对应颜色相比较得如下三个式子:
100 – pz=100cos(zeta3)
pycos(zeta1) - d2 - pxsin(zeta1)= 100sin(zeta3)
pxcos(zeta1) + pysin(zeta1)=0
三式联合求解得出
zeta1=-arctan(px/py)
zata3=arccos((100-pz)/100)
D2=pycos(zeta1)-pxsin(zeta1)-100*sin(zata3)
1. 建机器人
ToDeg = 180/pi;
ToRad = pi/180;
UX = [1 0 0]';
UY = [0 1 0]';
UZ = [0 0 1]';
Link= struct('name','Body' , 'th', 0, 'dz', 0, 'dy', 0, 'dx', 0, 'alf',90*ToRad,'az',UZ); % az
Link(1)= struct('name','Base' , 'th', 0*ToRad, 'dz', 0, 'dy', 0,'dx', 0, 'alf',0*ToRad,'az',UZ); %Base To 1
Link(2) = struct('name','J1' , 'th', 0*ToRad, 'dz', 100, 'dy', 0, 'dx', 0, 'alf',-90*ToRad,'az',UZ); %1 TO 2
Link(3) = struct('name','J2' , 'th', 90*ToRad, 'dz', 200, 'dy', 0, 'dx', 0, 'alf',90*ToRad,'az',UZ); %2 TO 3
Link(4) = struct('name','J3' , 'th', 0*ToRad, 'dz', 0, 'dy', 0, 'dx', 100, 'alf',0*ToRad,'az',UZ); %3 TO E
2.draw_6DOF_Workplace.m
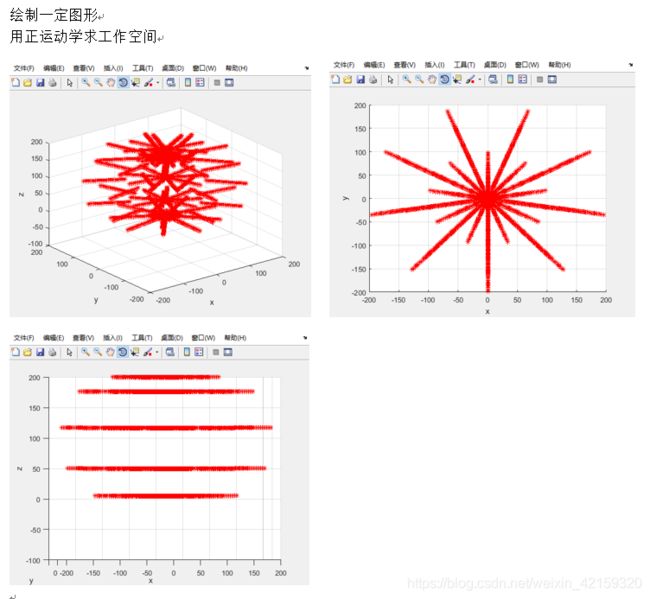
2. 画工作空间
close all; %删除其句柄未隐藏的所有图窗。
clear; %清除工作空间
ToDeg = 180/pi; %转化为度数
ToRad = pi/180; %转化为弧度
point1=[]; %设为矩阵
point2=[];
point3=[];
th_interval = 40; %弧间隔
z_interval = 4; %线间隔
th1=0; %为th1至th6设定初始值
th2=0;
th3=0;
global Link
num = 1;
for theta1=-180:th_interval:180 %循环画工作空间
for dt2=00:z_interval:100
for theta3=-180:th_interval:180
zq_robot_dh(th1+theta1,th2+dt2,th3+theta3,1); %,d4+dz4,th5+theta5,th6+theta6
point1(num) = Link(4).p(1); %用这个矩阵来存数据,这里共存三行数据
point2(num) = Link(4).p(2);
point3(num) = Link(4).p(3);
num = num + 1;
plot3(point1,point2,point3,'r*');hold on; %这里用了point1,point2,point3,而不用 point1(num),point2(num), point3(num)?
end
end
end
cla; %cla 从当前坐标区删除包含可见句柄的所有图形对象,把上面的图形清除。
plot3(point1,point2,point3,'r*'); %这里再画一个图形
axis([-400,400,-400,400,-400,400]); %设置轴范围和纵横比
grid on; %显示 gca 命令返回的当前坐标区或图的主网格线。主网格线从每个刻度线延伸。grid off 删除当前坐标区或图上的所有网格线。
3.zq_robot_qiunijie.m
3. 根据逆运动学方程求关节角度
%根据逆运动学方程求关节角度
function [ th1,d2,th3] = zq_robot_qiunijie( px,py,pz )
ToDeg = 180/pi;
ToRad = pi/180;
th1=-atan2(px,py); %逆运动学方程
th3=acos((100-pz)/100);
d2=py*cos(th1)-px*sin(th1)-100*sin(th3);
fprintf('th1=%4.2f \n',th1*ToDeg); %观察输出结果
fprintf('d2=%4.2f \n',d2);
fprintf('th3=%4.2f \n',th3*ToDeg);
end
4.draw_cube.m
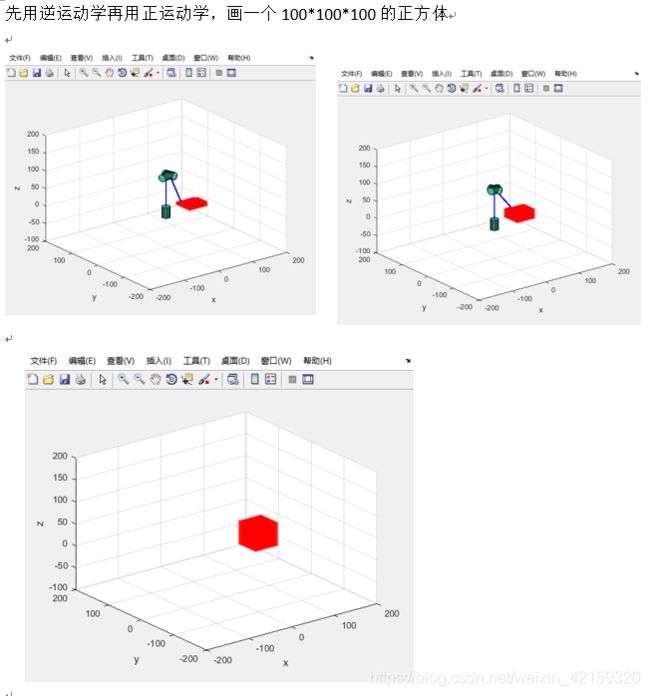
4. 画正方体(此处用到正、逆运动学)
%画正方体
close all;
clear;
ToDeg = 180/pi;
ToRad = pi/180;
point1=[]; %设为矩阵
point2=[];
point3=[];
num=1;
global Link
for z=0:5:50
for y=-25:5:25
for x=50:5:100
[th1,d2,th3]= zq_robot_qiunijie(x,y,z); %逆运动学
th1=th1*ToDeg;
th3=th3*ToDeg;
move=zq_robot_dh(th1,d2,th3,1); %正运动学
point1(num) = Link(4).p(1); %用这个矩阵来存数据,这里共存三行数据
point2(num) = Link(4).p(2);
point3(num) = Link(4).p(3);
plot3(point1,point2,point3,'r.');hold on; %这里用了point1,point2,point3,而不用 point1(num),point2(num), point3(num)?
fprintf('point1=%4.2f \n',point1(num)); %观察输出点的情况
fprintf('point2=%4.2f \n',point2(num));
fprintf('point3=%4.2f \n',point3(num));
num = num + 1;
end
end
end
grid on;
5.draw_writing
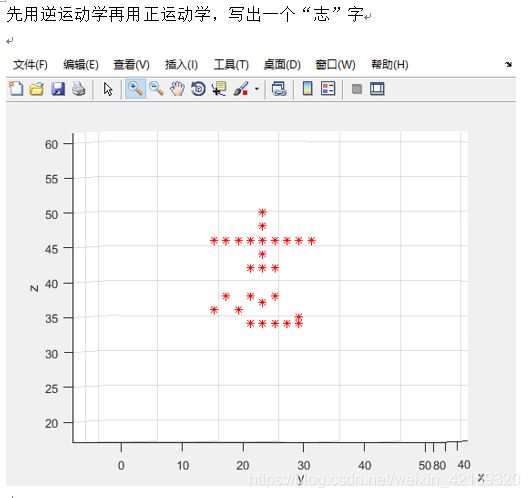
5. 写“志”字(此处用到正、逆运动学)
close all;
clear;
ToDeg = 180/pi;
ToRad = pi/180;
point1=zeros(100,1); %设为矩阵
point2=zeros(100,1);
point3=zeros(100,1);
num=1;
global Link
xx=50;
yy=[20;20;12;14;16;18;20;22;24;26;28;20;18;20;22;14;12;16;18;20;22;24;26;26;18;20;22];
zz=[50;48;46;46;46;46;46;46;46;46;46;44;42;42;42;38;36;36;34;34;34;34;35;34;38;37;38];
for i=1:1:27
[th1,d2,th3]= zq_robot_qiunijie(xx,yy(i),zz(i)); %求逆解
th1=th1*ToDeg;
th3=th3*ToDeg;
move=zq_robot_dh(th1,d2,th3,1);
point1(num) = Link(4).p(1); %用这个矩阵来存数据,这里共存三行数据
point2(num) = Link(4).p(2);
point3(num) = Link(4).p(3);
plot3(point1,point2,point3,'r*');hold on; %这里用了point1,point2,point3,而不用 point1(num),point2(num), point3(num)?
fprintf('point1=%4.2f \n',point1(num)); %观察输出点的情况
fprintf('point2=%4.2f \n',point2(num));
fprintf('point3=%4.2f \n',point3(num));
num = num + 1;
end
grid on;
6.Connect3D.m
function Connect3D(p1,p2,option,pt) %这是连接两个关节成一条杆的函数,Link(i).p表示第i个关节的空间位置。
h = plot3([p1(1) p2(1)],[p1(2) p2(2)],[p1(3) p2(3)],option); %画p1点到p2点的直线,p1,p2两点都是四行一列的矩阵,不过这里取前三行的值。option是线条颜色值。
set(h,'LineWidth',pt) %这里pt为线宽,即机器人杆的宽度。
7.DHfk6Dof_Workplace
function pic=DHfk6Dof_Workplace(th1,th2,th3,fcla,fplot) %这是用来画工作空间的函数内核 d4,th5,th6,
% close all
global Link
% zq_3dof_robot;
Build_3DOFRobot_Lnya;
radius = 10;
len = 20;
joint_col = 0;
plot3(0,0,0,'ro');
Link(2).th=th1*pi/180; %变成弧度,th1取至draw_6DOF_Workplace。
Link(3).th=th2*pi/180;
Link(4).th=th3*pi/180;
% p0=[0,0,0]';
for i=1:4
Matrix_DH_Ln(i); %生成关节链接的D-H矩阵。
end
for i=2:4
Link(i).A=Link(i-1).A*Link(i).A; %第i+1个矩阵乘第i个矩阵,矩阵右乘,把所有矩阵相乘。 Link(i)函数取至Matrix_DH_Ln(i)。
Link(i).p= Link(i).A(:,4); %取Link(i).A中所有行的第4列放到Link(i).p,把第i个关节的位置存在Link(i).p中。
Link(i).n= Link(i).A(:,1); %同上
Link(i).o= Link(i).A(:,2); %同上
Link(i).a= Link(i).A(:,3); %同上
Link(i).R=[Link(i).n(1:3),Link(i).o(1:3),Link(i).a(1:3)]; %把第i个关节的姿态存在 Link(i).R中
if fplot %当fplot为1时执行下面两个函数
Connect3D(Link(i-1).p,Link(i).p,'b',2); hold on; %'b',是指线条为蓝色,Link(i)函数取至Matrix_DH_Ln(i)。画杆 ,hold on 保留当前坐标区中的绘图,从而使新添加到坐标区中的绘图不会删除现有绘图。
DrawCylinder(Link(i-1).p, Link(i-1).R * Link(i).az, radius,len, joint_col); hold on; %画圆筒
end
end
grid on;
% view(134,12);
axis([-500,500,-500,500,-500,500]); %指定范围
xlabel('x');
ylabel('y');
zlabel('z');
drawnow;
pic=getframe;
if(fcla)
cla;
end
8.Matrix_DH_Ln
function Matrix_DH_Ln(i) %这个是D-H矩阵的算法函数
% Caculate the D-H Matrix
global Link
ToDeg = 180/pi;
ToRad = pi/180;
C=cos(Link(i).th);
S=sin(Link(i).th);
Ca=cos(Link(i).alf);
Sa=sin(Link(i).alf);
a=Link(i).dx; %distance between zi and zi-1
d=Link(i).dz; %distance between xi and xi-1
y=Link(i).dy;
Link(i).n=[C,S,0,0]';
Link(i).o=[-1*S*Ca,C*Ca,Sa,0]';
Link(i).a=[S*Sa, -1*C*Sa,Ca,0]';
Link(i).p=[a*C-y*S,a*S+y*C,d,1]'; %书本第57页的D-H矩阵
Link(i).R=[Link(i).n(1:3),Link(i).o(1:3),Link(i).a(1:3)];%把上面D-H矩阵前面的3*3矩阵存起来
Link(i).A=[Link(i).n,Link(i).o,Link(i).a,Link(i).p];%把第i到i+1的D-H矩阵存进Link(i).A
9.DrawCylinder.m
function h = DrawCylinder(pos, az, radius,len, col) %这是个画圆筒(关节)的函数
% draw closed cylinder
%
%******** rotation matrix
az0 = [0;0;1];
ax = cross(az0,az);
ax_n = norm(ax);
if ax_n < eps
rot = eye(3);
else
ax = ax/ax_n;
ay = cross(az,ax);
ay = ay/norm(ay);
rot = [ax ay az];
end
%********** make cylinder
% col = [0 0.5 0]; % cylinder color
a = 20; % number of side faces
theta = (0:a)/a * 2*pi;
x = [radius; radius]* cos(theta);
y = [radius; radius] * sin(theta);
z = [len/2; -len/2] * ones(1,a+1);
cc = col*ones(size(x));
for n=1:size(x,1)
xyz = [x(n,:);y(n,:);z(n,:)];
xyz2 = rot * xyz;
x2(n,:) = xyz2(1,:);
y2(n,:) = xyz2(2,:);
z2(n,:) = xyz2(3,:);
end
%************* draw
% side faces
h = surf(x2+pos(1),y2+pos(2),z2+pos(3),cc);
for n=1:2
patch(x2(n,:)+pos(1),y2(n,:)+pos(2),z2(n,:)+pos(3),cc(n,:));
end
10.zq_robot_dh.m
function pic = zq_robot_dh( th1,distance,th3,fcla )
%UNTITLED4 此处显示有关此函数的摘要
% 此处显示详细说明
global Link
zq_3dof_robot;
radius = 10;
len = 30;
joint_col = 0;
plot3(0,0,0,'ro');
Link(2).th=th1*pi/180;
Link(3).dz=distance;
Link(4).th=th3*pi/180;
p0=[0,0,0]';
for i=1:4
Matrix_DH_Ln(i);
end
for i=2:4
Link(i).A=Link(i-1).A*Link(i).A;
Link(i).p= Link(i).A(:,4);
Link(i).n= Link(i).A(:,1);
Link(i).o= Link(i).A(:,2);
Link(i).a= Link(i).A(:,3);
Link(i).R=[Link(i).n(1:3),Link(i).o(1:3),Link(i).a(1:3)];
Connect3D(Link(i-1).p,Link(i).p,'b',2); hold on;
DrawCylinder(Link(i-1).p, Link(i-1).R * Link(i).az,radius,len, joint_col); hold on;
end
grid on;
% view(134,12);
axis([-200,200,-200,200,-100,200]);
xlabel('x');
ylabel('y');
zlabel('z');
drawnow;
pic=getframe;
if(fcla)
cla;
end
end
11.zhengyundongxue.m
%dh矩阵函数
function [ result ] = zhengyundongxue( A )
%ZHENGYUNDONGXUE 此处显示有关此函数的摘要
% 此处显示详细说明
zeta=A(1);
d=A(2);
a=A(3);
alf=A(4);
result=[cos(zeta) -sin(zeta)*cos(alf) sin(zeta)*sin(alf) a*cos(zeta);
sin(zeta) cos(zeta)*cos(alf) -cos(zeta)*sin(alf) a*sin(zeta);
0 sin(alf) cos(alf) d;
0 0 0 1];
end
12.jisuanzhengyundong.m
%这是用来求正运动学中各个dh矩阵的
syms pi d2 zeta1 zeta2 zeta3 A4 a1 a2 a3 nx ny nz ox oy oz ax ay az px py pz U1;
%p1=[0 d2 0 0];
p1=[zeta1 100 0 -pi/2];
A1=zhengyundongxue(p1);
A1=simplify(A1)
%p2=[zeta2 0 100 pi/2];
p2=[pi/2 d2 0 pi/2];
A2=zhengyundongxue(p2);
A2=simplify(A2)
%p3=[zeta3 0 100 0];
p3=[zeta3 0 100 0];
A3=zhengyundongxue(p3);
A3=simplify(A3)
A4=A1*A2*A3;
A4=simplify(A4)
a1=inv(A1); %求逆
a2=inv(A2);
a3=inv(A3);
a1=simplify(a1)
a2=simplify(a2)
a3=simplify(a3)
U=[nx ox ax px;ny oy ay py;nz oz az pz;0 0 0 1];%设出要求的矩阵U
U1=a2*a1*U;
U1=simplify(U1)
13.Computer_T.m
close all;
clear;
ToDeg = 180/pi;
ToRad = pi/180;
syms theta d a alpha y;
T1 = [cos(theta) -sin(theta) 0 0; sin(theta) cos(theta) 0 0; 0 0 1 0; 0 0 0 1];
T2 = [1 0 0 0; 0 1 0 0; 0 0 1 d; 0 0 0 1];
T3 = [1 0 0 a; 0 1 0 0; 0 0 1 0; 0 0 0 1];
T4 = [1 0 0 0; 0 cos(alpha) -sin(alpha) 0; 0 sin(alpha) cos(alpha) 0; 0 0 0 1];
Ty = [1 0 0 0; 0 1 0 y; 0 0 1 0; 0 0 0 1];
T = T1 * T2 * Ty * T3 * T4
syms theta1 theta2 theta3 d4 theta5 theta6
theta=theta1;d=100;y=0;a=0;alpha = -90*ToRad;
A1 = subs(T)
theta=-90*ToRad+theta2;d=0;y=0;a=100;alpha = 0;
A2 = subs(T)
theta=theta3;d=0;y=50;a=0;alpha = -90*ToRad;
A3 = subs(T)
% theta=0;d=50+d4;y=0;a=0;alpha = 0;
% A4 = subs(T)
% theta=theta5;d=50;y=0;a=0;alpha = 90*ToRad;
% A5 = subs(T)
% theta=90*ToRad+theta6;d=0;y=0;a=50;alpha = 0;
% A6 = subs(T)
A = A1 * A2 * A3 %* A4 * A5 * A6
上面代码比较多,逐一放到matlab中运行一下,看看各个代码的效果如何。