Rinex文件格式中知识点&卫星导航知识点

一、观测数据

1、观测值

其中观测值（伪距、载波相位）的格式为：

m( F14. 3, I1, I1)

表达意思：这一行的内容从第 1 列开始依次是宽度为14位、小数点后有3位的单精度浮点数、宽度为 1 的整型、宽度为 1 的整型。

示例：

C1=24465528.830；LLI整数值为4，二进制表示为：00000100b；S/N整数值为：5；

L1=128567213.018；LLI整数值为4，二进制表示为：00000100b；S/N整数值为：5；

其中对于LLI：

      LLI的范围为0～7。0或空格表示正常或未知;bit0置1表示在前一历元与当前历元之间发生了失锁,可能有周跳;bit1置1表示该卫星的波长因子与前面WAVELENGTHFACTL1/2记录中的定义相反,仅对当前历元有效;bit2置1表示为反欺骗(AS)下的观测值(可能会受到噪声增加的影响)。其中,bit0和bit1仅用于相位。

即此时的L1不存在周跳！

 

 

 

二、导航电文

 

三、其他：

1、相关信息：

轨道：
GEO：地球静止轨道；MEO：中地球轨道；IGSO：倾斜地球同步轨道。
PRN：伪随机噪声码（Pseudo random noise code, PRN）
SVN：空间飞行器编号（Space vehicle number, SVN）
火箭：
CZ-3A：长征三号甲；CZ-3B：长征三号乙；CZ-3C：长征三号丙。
链接：https://blog.csdn.net/m0_37362454/article/details/93887012

2、电离层穿刺点与穿刺点星下点

       电离层分布在离地面约 50～1000km 的高度范围内，且不同高度电子密度不相同。卫星导航定位用户往往只关心总电子含量，而非电子的分布密度，因此在 GNSS 电离层研究领域常常引入单层假设，即将电离层单层假设是二维 TEC 模型建立的基础。其基本原理是忽略电子密度在垂直方法的分布，假设电离层集中于地球上方某一高度处的无限薄的一个薄层上面。在这一假设之下，电离层成为只具有总电子含量的位置、时间分布特征的物理量，从而可以以位置和时间为自变量，并将总电子含量看做这几个自变量的函数，进而对一定时间、空间范围之内的电离层变化进行数学表达，可以通过某些数学模型，如多项式模型、球谐函数模型等进行曲面拟合。

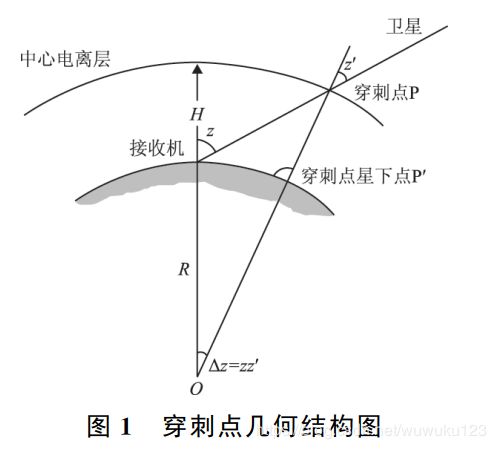
        单层假设中，信号传播路径与中心电离层的交点称为穿刺点，如图１所示，Ｏ为地心，Ｐ为穿刺点，Ｐ′为穿刺点对应的星下点，ｚ、ｚ′分别为接收机和穿刺点处卫星的天顶距，Δｚ为对应地心角。

3、Kalman中状态协方差矩阵从卡尔曼增益k的表达式

从kalman增益Km的表达式：

 
       可以看出，当R的对角线上某元素很大时，对应的Km中的元素会很小，说明由对应的观测量导致的δx很小；如果P的某元素很小时，对应的Km中的元素很小，说明此时的δx也很小。

       通过上述分析，我们可以看出卡尔曼滤波每次对系统状态的更新是基于当前系统状态的不确定度和观测量的不确定度之间的折中。如果当前的系统状态估计的不确定度为零，即当前的系统状态估计非常可靠，则由观测量导致的更新将非常小；反之，如果观测量的不确定度非常低，即观测量非常可信，则系统状态的更新将主要由观测量决定。所以卡尔曼滤波是一种自适应的过程，卡尔曼滤波中的P矩阵提供了对系统状态误差的方差估计，即
 
       在实际中，P矩阵往往被用来对x的状态估计误差作出评估，如果P矩阵中的元素比较大，则说明对应的系统状态量可信度较低；反之，则说明对应的系统状态量可信度较高。
 

 

 

 

 

 

 

 

参考：

1、rinex数据格式

2、《多卫星导航系统电离层穿刺点分布的仿真分析》

3、《北斗/GPS双模软件接收机原理与实现技术》