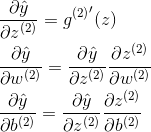花书+吴恩达深度学习（一）前馈神经网络（多层感知机 MLP）
目录
0. 前言
1. 每一个神经元的组成
2. 梯度下降改善线性参数
3. 非线性激活函数
4. 输出单元
4.1. 线性单元
4.2. sigmoid 单元
4.3. softmax 单元
5. 神经网络宽度和深度的选择
6. 前向传播和反向传播
如果这篇文章对你有一点小小的帮助，请给个关注，点个赞喔~我会非常开心的~
花书+吴恩达深度学习（一）前馈神经网络（多层感知机 MLP）
花书+吴恩达深度学习（二）非线性激活函数（ReLU, maxout, sigmoid, tanh）
花书+吴恩达深度学习（三）反向传播算法 Back Propagation
花书+吴恩达深度学习（四）多分类 softmax
0. 前言
前馈神经网络（feedforward neural network），又称作深度前馈网络（deep feedforward network）、多层感知机（multilayer perceptron，MLP）。
信息流经过 
的函数，流经中间的计算过程，最终达到输出 
，所以被称为是前向的。
在模型的输出和模型本身之间并没有反馈连接。
神经网络可以表示成如下图所示（图源：吴恩达深度学习）：
这是一个两层的神经网络，左侧是输入层，通常不算入网络层数的计算中，中间被称为隐藏层，右侧是输出层。
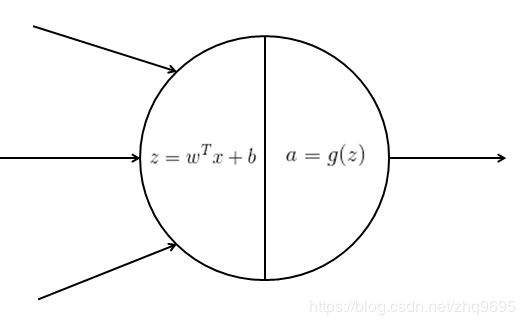
1. 每一个神经元的组成
每一个神经元由一个线性拟合和一个非线性激活函数组成。
假设，前一层的输入为 ，线性拟合表示为 
，权重乘以每一个特征值，再加上一个截距。非线性激活函数表示为 
，
为神经元的输出，也是传入下一层神经元的输入。
注：如果不使用非线性激活函数，那么每一个神经元都是线性的，导致一个神经网络多个神经元的线性组合仍然是线性的，最终的输出也是线性拟合，无法泛化非线性的问题。
2. 梯度下降改善线性参数
我们已知，使用梯度下降的方法（使得参数往负梯度的方向移动），可以使参数更好的匹配数据。
通常我们会定义一个代价函数（损失函数），函数值越大表示精确率越不准，损失越大。
大多数神经网络使用最大似然作为代价函数：
![J(\theta)=-\mathbb{E}[\ \log\ p_{model}(y\mid x)\ ]](http://img.e-com-net.com/image/info8/4b46faef0bf34296857feb300cbcf94d.gif){kind=small}
如果假设模型的分布服从高斯分布，则代价函数可采用均方误差表示：
![J(\theta)=\frac{1}{2}\mathbb{E}[\ \left\|y-f(x;\theta)\right\|^2\ ]](http://img.e-com-net.com/image/info8/286a1113e0e9474db7f1783cb3744bd3.gif){kind=small}
我们已知，梯度是对函数的各个方向求导，如果函数的梯度较小， 则参数的移动也会较小。
这就要求代价函数的梯度必须足够大和具有足够的预测性。
如果代价函数梯度不够大，就会造成梯度饱和的困难。
同时，如果参数过小，也会造成梯度较小，称为梯度消失。
如果参数过大，也会造成梯度较大，称为梯度爆炸。
将所有的权重初始化为随机小的数是很重要的。一种指导是将其初始化为：
![W^{[l]}=\textup{np.random.randn}(W^{[l]}.shape)*\textup{np.sqrt}(\frac{2}{n^{[l-1]}})](http://img.e-com-net.com/image/info8/05f1e3de64354c368c43958630525101.gif){kind=small}
对于大多数非线性问题，代价函数通常是非凸函数，这就表示梯度下降一般不能优化至全局最小值，仅能使得函数达到一个非常小的值。
3. 非线性激活函数
如果不使用非线性激活函数，那么每一个神经元都是线性的，导致一个神经网络多个神经元的线性组合仍然是线性的，最终的输出也是线性拟合，无法泛化非线性的问题。
大多数隐藏单元的区别仅仅在于激活函数的不同。
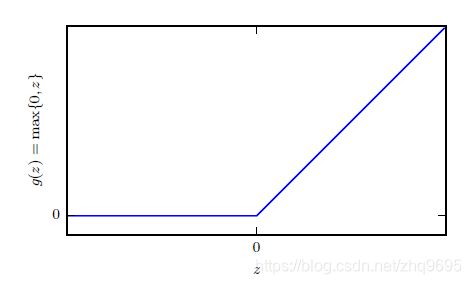
大多数隐藏单元采用 ReLU 整流线性单元（rectified linear unit），
：
如上图所示（图源：深度学习），函数仍然非常接近线性，因此它保留了许多线性模型易于使用梯度优化的属性。
除此之外还有许多的激活函数，可移步至我的博客。
4. 输出单元
4.1. 线性单元
在输出单元处，不设置激活函数，直接应用 输出，被称作线性单元。
4.2. sigmoid 单元
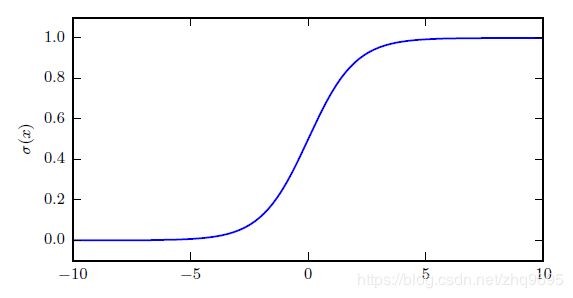
针对二分类的问题，通常需要把输出限制在 
之间，表示针对某一类别的概率。
sigmoid 单元正满足这一特性：
当使用 sigmoid 函数作为输出单元激活函数时，通常代价函数使用最大似然。
因为从图中可知，sigmoid 函数在自变量很大或者很小的时候，具有梯度饱和的问题。
而最大似然的 
正好可以抵消 sigmoid 函数中的 
。
4.3. softmax 单元
针对多分类问题的时候，softmax 函数可以表示 
个不同类别上的概率分布。
softmax 函数表示为：
softmax 函数有多个输出值，当不同值之间差异变得极端的时候，输出值也可能饱和。
当使用最大化对数似然的时候，同 sigmoid 函数一样， 抵消 ，更适合梯度下降：
5. 神经网络宽度和深度的选择
万能近似定理（universal approximation theorem）表示，一个前馈神经网络如果具有线性输出层和至少一层具有任何一种挤压性质的激活函数的隐藏层，只要给予网络足够数量的隐藏单元，它可以以任意精度来近似任何从一个有限维空间到另一个有限维空间的可测函数，前馈神经网络的导数也可以任意好的近似函数的导数。
用深度整流网络表示的函数可能需要浅层网络指数级别的隐藏单元才能表示，所以更深的模型似乎确实在广泛的任务中泛化的更好。
6. 前向传播和反向传播
在一个神经网络中：
输入 进入第一层网络，每个神经元计算 
，输出至第二层网络，
，最终产生输出 
。这种由输入 不断计算，传播至输出产生 
的过程称为前向传播（forward propagation）。
已知通过计算梯度，可以改善参数对数据的匹配。
计算第二层网络的梯度，可以改善第二层网络的参数：
计算第一层网络的梯度，可以改善第一层网络的参数：
根据导数的链式法则，每一层梯度的计算都使用到了后面一层梯度的计算结果，这种从后面一层不断计算梯度，然后传递到前面一层再计算梯度，直到输入的过程，称为反向传播（back propagation）。
关于反向传播算法更详细的理解，可移步至我的博客。
如果这篇文章对你有一点小小的帮助，请给个关注，点个赞喔~我会非常开心的~