【算法】并查集(Union-Find)的理解和最佳实践 附代码

并查集（Union-Find）常常被用来解决动态连通性问题。

1. 动态连通性

1.1 概念

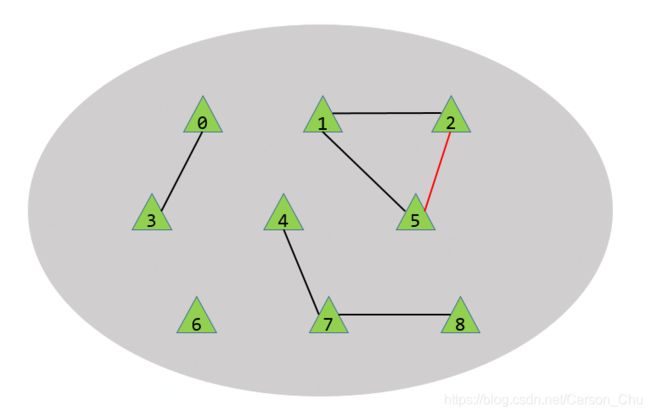
首先用一张图来说明什么是动态连通性，如下图所示，有9个村落，有黑线连接表示两个村落是互通的。假设输入了一组整数对pairs，如(0,3)(1,2)等等，每对整数对代表这两个村落站点sites是连通的。随着sites的不断建设，整个图的连通性也会发生变化，对于已经连通的sites则直接忽略，如图中的(2,5)。

1.2 应用场景

• 网络连接判断：

如果每个pair中的两个整数分别代表一个网络节点，那么该pair就是用来表示这两个节点是需要连通的。那么为所有的pairs建立了动态连通图后，就能够尽可能少的减少布线的需要，因为已经连通的两个节点会被直接忽略掉。

• 变量名等同性(类似于指针的概念)：

在程序中，可以声明多个引用来指向同一对象，这个时候就可以通过为程序中声明的引用和实际对象建立动态连通图来判断哪些引用实际上是指向同一对象。

2. 问题建模

对于连通的所有节点，我们可以认为它们属于一个组，因此不连通的节点必然就属于不同的组。随着pair的输入，我们需要首先判断输入的两个节点是否连通。如何判断呢？按照上面的假设，我们可以通过判断它们属于的组，然后看看这两个组是否相同，可以使用数组来表示这一层关系，数组的索引是节点的整数表示，而相应的值就是该节点的组号了。该数组可以初始化为：

		int[] pairs = new int[size];
        for (int i = 0; i < size; i++) {
            pairs[i] = i;
        }

我们可以初步设计相应的API：

Tips：
如果想使用其它数据类型，如字符串，可以用hash表进行映射。

3. 算法设计

3.1 初步设计——Quick-Find算法

首先确定存储的数据结构采用数组，先附代码：

/**
 * @author Carson Chu
 * @date 2020/1/22 10:04
 */
public class UnionFind {
    /* save all components,the index is component,and the corresponding value is the group for the component */
    private int[] components;
    /* number of sites */
    private int length;

    public UnionFind(int size) {
        /* initialize component array.*/
        length = size;
        components = new int[size];
        for (int i = 0; i < size; i++) {
            components[i] = i;
        }
    }

    public int count() {
        return length;
    }

    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    public int find(int p) {
        return components[p];
    }

    public void union(int p, int q) {
        // find the group for p and q
        int pGroup = find(p);
        int qGroup = find(q);
        // if p and q have the same group,then return
        if (pGroup == qGroup) {
            return;
        }
        /* go through it once and change the group to make them equal */
        for (int i = 0; i < components.length; i++) {
            if (components[i] == pGroup) {
                components[i] = qGroup;
            }
        }
        length--;
    }
}

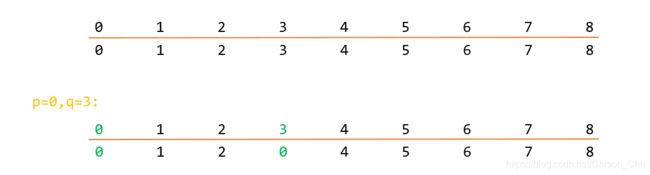
首先调用构造函数的时候，对整个数组进行初始化，索引保存的就是元素，对应的值就是所属的组别。初始化结束后，每个元素有一个单独的组。假设p=0,q=3，想将0和3两个元素对应的组整合成一个组中，需要调用union函数，在一次遍历将组号3都改成0（也可以将0改成3，但是保证每次操作时使用相同的规则，如每次都将组号大的修改为组号小的值），如下图：

存在的问题：
上述代码的find方法十分高效，因为仅仅需要一次数组读取操作就能够找到该节点的组号，时间复杂度仅为O(1)。但是问题随之而来，对于需要添加新路径的情况，因为并不能确定哪些节点的组号需要被修改，因此就必须对整个数组进行遍历，找到需要修改的节点，逐一修改，这一下每次添加新路径带来的复杂度就是线性关系了，如果要添加的新路径的数量是M，节点数量是N，那么最后的时间复杂度就是MN，显然是一个平方阶的复杂度，想要解决这个问题，关键就是要提高union方法的效率，让它不再需要遍历整个数组。

3.2 优化设计——Quick-Union算法

上述Quick-Find算法的问题在于，每个节点所属的组号都是各自独立的，当涉及到修改的时候，除了遍历、修改之外别无他法。为了将节点更好的组织起来，需要将组号相同的节点放置在一起，联想数据结构中查找、修改效率最高的数据结构当属树了。
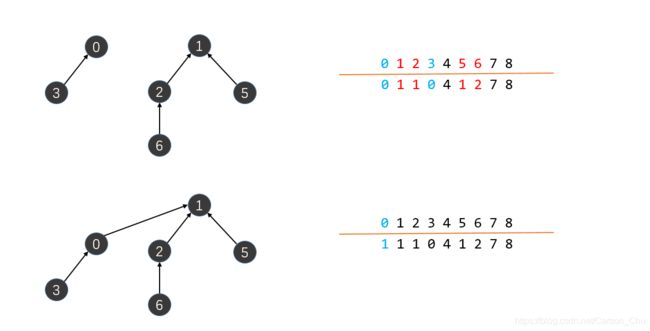
这里不去考虑修改底层数据结构，即还是用数组表示。采用parent-link的方式将所有节点组织起来，即component[p]的值就是节点p的父节点的序号，如节点p是树根的话，那么component[p]=p。直观的过程如图：

和之前的Quick-Find算法相比，只需要优化find和union两个方法：

public int find(int p) {
        /* find the root for p */
        while (p != components[p]) {
            p = components[p];
        }
        return p;
    }

    public void union(int p, int q) {
        // get the root for p and q
        int pRoot = find(p);
        int qRoot = find(q);
        // if p and q have the same group,then return
        if (pRoot == qRoot) {
            return;
        }
        /* 将一棵树变成另一棵树的子树 */
        components[pRoot] = components[qRoot];
        length--;
    }

事实上，树这种数据结构容易出现极端情况，因为在建树的过程中，树的最终形态严重依赖于输入数据本身的性质，比如数据是否排序。那么应该如何去规避树退化成链表这种风险呢？观察上述代码，不难发现:components[pRoot] = components[qRoot];这句看上去很奇怪，强行将两棵树融合（这也属于一种硬编码），这样做其实是不合理的，因为假如q所在的树要比p所在的树的规模大很多的话，融合之后的树就变得头重脚轻了。为了解决这个问题，我们应该采用加权的方式，即每次都保证让size小的树和size大的树去进行合并。我们可以通过使用额外的一个数组来记录每个组的大小，并在构造函数中进行初始化。

3.3 进一步优化——Weighted Quick-Union算法

public UnionFind(int size) {
        /* initialize component array.*/
        length = size;
        components = new int[size];
        for (int i = 0; i < size; i++) {
            components[i] = i;
        }
        /* initialize component size */
        componentsSize = new int[size];
        for (int i = 0; i < size; i++) {
            /* 初始化时，每个组的大小都是1 */
            componentsSize[i] = 1;
        }
    }

初始化完成之后，调用union方法每次都要判断合并的两棵树的大小,然后再将小树合并到大树下：

public void union(int p, int q) {
        // get the root for p and q
        int pRoot = find(p);
        int qRoot = find(q);
        // if p and q have the same group,then return
        if (pRoot == qRoot) {
            return;
        }
        /* 将小树作为大树的子树 */
        if (componentsSize[pRoot] < componentsSize[qRoot]) {
            components[pRoot] = qRoot;
            componentsSize[qRoot] += componentsSize[pRoot];
        } else {
            components[qRoot] = pRoot;
            componentsSize[pRoot] += componentsSize[qRoot];
        }
        length--;
    }

可以发现，通过componentsSize数组决定如何对两棵树进行合并之后，最后得到的树的高度大幅度减小了。这是十分有意义的，因为在Quick-Union算法中的任何操作，都不可避免的需要调用find方法，而该方法的执行效率依赖于树的高度。树的高度减小了，find方法的效率就增加了，从而也就增加了整个Quick-Union算法的效率。

3.4 最终优化方案——Weighted Quick-Union With Path Compression算法

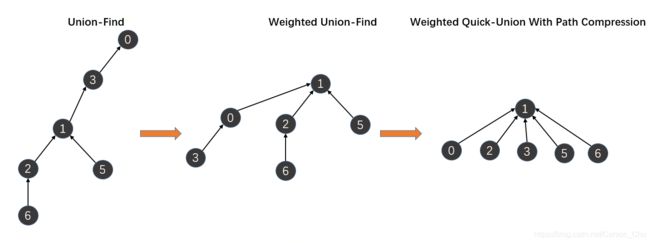
上述已经实现了树结构的平衡，规避了树严重失衡的问题，但是细想，要是能实现树的扁平化，即最终保证所有的节点都共享唯一的根节点，这样的话find查询效率将进一步提升，如图所示：

理想很丰满，但具体应该怎么实现呢？其实也不难，就是在寻找根节点的同时对路径进行压缩，让遍历到的所有节点最终都指向根结点，从而实现树的扁平化。根据分析结果可知，只需要在find方法中优化：

public int find(int p) {
        /* find the root for p */
        while (p != components[p]) {
            /* 将p节点的父节点设置为它的爷爷节点 */
            components[p] = components[components[p]];
            p = components[p];
        }
        return p;
    }

附上述算法的时间复杂度：

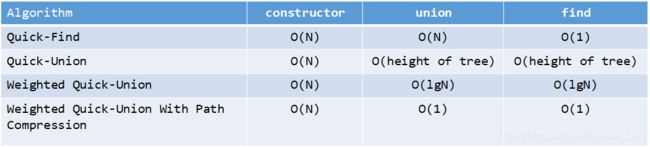
在项目开发中使用平方阶的算法是极不合适的（也许你认为现阶段数据量小，平方阶算法响应也很快，但是要养成良好的开发习惯，如果之后数据量暴涨，重构代码不是一个明智的方案，应该在一开始就想到潜在的风险并规避。），比如上述Quick-Find算法，通过发不断发现问题并改进，得到了Quick-Union算法及其多种优化方案，最终得到了令人满意的解决方案。当然，如果需要的功能不仅仅是检测两个节点是否连通，还需要在连通时得到具体的路径，那么就需要用到深度优先或者广度优先算法了，关于这点暂不作讨论。

4. 并查集应用示例

问题描述：
包围区域问题：
Given a 2D board containing ‘X’ and ‘O’ (the letter O), capture all regions surrounded by ‘X’.
A region is captured by flipping all 'O’s into 'X’s in that surrounded region.
Example:
X X X X
X O O X
X X O X
X O X X
After running your function, the board should be:
X X X X
X X X X
X X X X
X O X X
解决方案：

/**
 * @author Carson Chu
 * @date 2020/1/22 15:28
 */
public class Solution {

    private static int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

    /**
     * Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'.
     * A region is captured by flipping all 'O's into 'X's in that surrounded region.
     * Example:
     * X X X X
     * X O O X
     * X X O X
     * X O X X
     * After running your function, the board should be:
     * X X X X
     * X X X X
     * X X X X
     * X O X X
     * Explanation:
     * Surrounded regions shouldn’t be on the border, which means that any 'O' on the border of the board are not flipped to 'X'.
     * Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'.
     * Two cells are connected if they are adjacent cells connected horizontally or vertically.
     *
     * @param board
     */
    public void solve(char[][] board) {
        if (board == null || board.length == 0) {
            return;
        }

        UnionFindSet unionFindSet = new UnionFindSet(board);
        int rows = board.length, cols = board[0].length;
        int dummyBorder = rows * cols;

        for (int x = 0; x < rows; x++) {
            for (int y = 0; y < cols; y++) {
                if (board[x][y] == 'O') {
                    int borderO = x * cols + y;
                    if (x == 0 || x == rows - 1 || y == 0 || y == cols - 1) {
                        unionFindSet.union(dummyBorder, borderO);
                        continue;
                    }
                    for (int[] dir : directions) {
                        int nx = x + dir[0];
                        int ny = y + dir[1];
                        if (nx >= 0 && ny >= 0 && nx < rows && ny < cols && board[nx][ny] == 'O') {
                            int neighbor = nx * cols + ny;
                            unionFindSet.union(borderO, neighbor);
                        }
                    }
                }
            }
        }

        for (int x = 0; x < rows; x++) {
            for (int y = 0; y < cols; y++) {
                if (board[x][y] == 'O' && unionFindSet.find(x * cols + y) != unionFindSet.find(dummyBorder)) {
                    board[x][y] = 'X';
                }
            }
        }
    }
}

class UnionFindSet {
    int[] root;
    int[] size;

    public UnionFindSet(char[][] board) {
        int rows = board.length, cols = board[0].length;
        root = new int[rows * cols + 1];

        for (int x = 0; x < rows; x++) {
            for (int y = 0; y < cols; y++) {
                if (board[x][y] == 'O') {
                    int id = x * cols + y;
                    root[id] = id;
                }
            }
        }
        root[rows * cols] = rows * cols;
        size = new int[rows * cols + 1];
        for (int i = 0; i < rows * cols + 1; i++) {
            size[i] = 1;
        }
    }

    public int find(int x) {
        while (x != root[x]) {
            root[x] = root[root[x]];
            x = root[x];
        }
        return x;
    }

    public void union(int x, int y) {

        int rootX = find(x);
        int rootY = find(y);
        if (rootX == rootY) {
            return;
        }
        if (size[rootX] < size[rootY]) {
            root[rootX] = rootY;
            size[rootY] += size[rootX];
        } else {
            root[rootY] = rootX;
            size[rootX] += size[rootY];
        }
    }
}

参考阅读

并查集详解（超级简单有趣~~就学会了）