Python小白 Leetcode刷题历程 No.51-No.55 N皇后、N皇后Ⅱ、最大子序和、螺旋矩阵、跳跃游戏 (有题干 有代码 有思路心得)
文章目录
- Python小白 Leetcode刷题历程 No.51-No.55 N皇后、N皇后Ⅱ、最大子序和、螺旋矩阵、跳跃游戏
- 写在前面:
- No.51.N皇后
- No.52.N皇后Ⅱ
- No.53.最大子序和
- No.54.螺旋矩阵
- No.55.跳跃游戏
Python小白 Leetcode刷题历程 No.51-No.55 N皇后、N皇后Ⅱ、最大子序和、螺旋矩阵、跳跃游戏
写在前面:
作为一个计算机院的大学生,总觉得仅仅在学校粗略的学习计算机专业课是不够的,尤其是假期大量的空档期,作为一个小白,实习也莫得路子,又不想白白耗费时间。于是选择了Leetcode这个平台来刷题库。编程我只学过基础的C语言,现在在自学Python,所以用Python3.8刷题库。现在我Python掌握的还不是很熟练,算法什么的也还没学,就先不考虑算法上的优化了,单纯以解题为目的,复杂程度什么的以后有时间再优化。计划顺序五个题写一篇日志,希望其他初学编程的人起到一些帮助,写算是对自己学习历程的一个见证了吧。
有一起刷LeetCode的可以关注我一下,我会一直发LeetCode题库Python3解法的,也可以一起探讨。
觉得有用的话可以点赞关注下哦,谢谢大家!
········································································································································································
题解框架:
1.题目,难度
2.题干,题目描述
3.题解代码(Python3(不是Python,是Python3))
4.或许有用的知识点(不一定有)
5.解题思路
6.优解代码及分析(当我发现有比我写的好很多的代码和思路我就会写在这里)
········································································································································································
No.51.N皇后
题解代码(Python3.8)
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
res=[]
if n == 0:
return res
nums = [ i for i in range(n)]
col = set()
master = set()
slave = set()
stack = []
def backtrack(row):
if row == n:
board = solution(stack,n)
res.append(board)
return
for i in range(n):
if (i not in col) and (row+i not in master) and (row-i not in slave):
stack.append(nums[i])
col.add(i)
master.add(row+i)
slave.add(row-i)
backtrack(row+1)
stack.pop()
col.remove(i)
master.remove(row+i)
slave.remove(row-i)
def solution(stack,n):
return ['.'*stack[i] + 'Q' + '.'*(n-stack[i]-1) for i in range(n)]
backtrack(0)
return res
解题思路:
这道题是树形结构,且需要剪枝,于是我们采用回溯算法。按照回溯算法的模板,本题我们将行(row)作为回溯函数的变量,套用回溯算法的模板,则回溯算法的三个组成部分分别为:
1.回溯出口:行数row==n,将该情况的解法储存进结果res中;
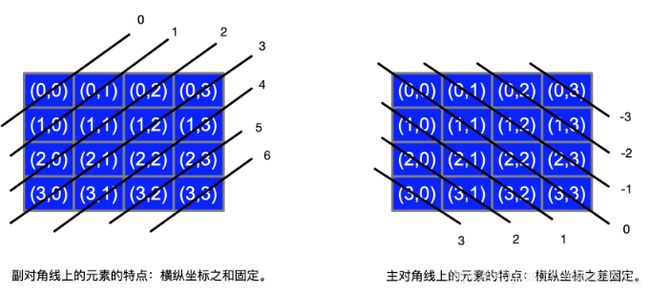
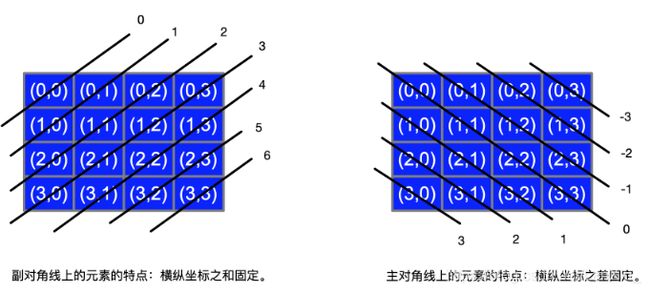
2.回溯主体:如果对于该行的列位置i,如果i满足无列冲突(因为是逐行回溯,因此必定不会行冲突)、无斜线冲突(横纵坐标之和之差都不冲突),则记录该位置的行(记录两次,一个是列表形式为了生成解,另一个是set形式为了判断是否冲突)、横纵坐标和、横纵坐标差,之和执行回溯函数backtrack(row+1);
3.状态返回:说明已经结束了该分支的回溯,则删除刚才记录的该位置的行、横纵坐标和、横纵坐标差。
为满足回溯函数,我们考虑创建一个从1到n的n元素的列表,和列、横纵坐标和、横纵坐标差的空set,来判断是否冲突;我们用一个列表,储存皇后在每一行的列位置,最后定义一个函数,将这个列表转换成棋盘格式的解,最后返回res即可。
No.52.N皇后Ⅱ
题解代码(Python3.8)
class Solution:
def totalNQueens(self, n: int) -> int:
res=[]
if n == 0:
return res
col = set()
master = set()
slave = set()
def backtrack(row):
if row == n:
res.append('count')
return
for i in range(n):
if (i not in col) and (row+i not in master) and (row-i not in slave):
col.add(i)
master.add(row+i)
slave.add(row-i)
backtrack(row+1)
col.remove(i)
master.remove(row+i)
slave.remove(row-i)
backtrack(0)
return len(res)
解题思路:
这道题的思路其实和上一题‘No.51.N皇后’基本一致,而且这道题比上一题‘No.51.N皇后’简单,即阉割版;上一题‘No.51.N皇后’需要我们写出所有解法的内容,本题只需写出解的数量即可。
这道题是树形结构,且需要剪枝,于是我们采用回溯算法。按照回溯算法的模板,本题我们将行(row)作为回溯函数的变量,则回溯算法的三个组成部分分别为:
1.回溯出口:行数row==n,将解的个数res+=1;
2.回溯主体:如果对于该行的列位置i,如果i满足无列冲突(因为是逐行回溯,因此必定不会行冲突)、无斜线冲突(横纵坐标之和之差都不冲突),则记录该位置的行、横纵坐标和、横纵坐标差,之和执行回溯函数backtrack(row+1);
3.状态返回:说明已经结束了该分支的回溯,则删除刚才记录的该位置的行、横纵坐标和、横纵坐标差。
为满足回溯函数,我们考虑创建列、横纵坐标和、横纵坐标差的空set,来判断是否冲突,并初始化res=0,最后返回res。
No.53.最大子序和
题解代码(Python3.8)
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
l=len(nums)
if l==0:
return 0
dp=[0 for _ in range(l)]
dp[0]=nums[0]
for i in range(1,l):
dp[i] = max(dp[i-1]+nums[i],nums[i])
return max(dp)
或许有用的知识点:
这道题可用使用动态规划的方法。
这道题可用使用分治算法来解决(更为精妙,我会在‘优解代码及分析’详细说明)。
解题思路:
这道题是求最优化解的问题,且满足动态规划问题的条件,于是我们用动态规划的方法来做。这道题套用动态规划的模板,的到动态规划的三要素分别为:
状态:从头到第i个元素,能得到的最大子序和为dp[i];则从头到第i+1个元素,能得到的最大子序和为的(dp[i]+nums[i+1])和(nums[i+1])中的最大数值。
状态转移方程:dp[i] = max(dp[i-1]+nums[i],nums[i])
边界条件:dp[0]=nums[0]
之后对列表从头到尾动态规划即可。
复杂度:
时间复杂度: O(N)
空间复杂度: O(1)
优解代码及分析:
优解代码(Python3.8)
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
l=len(nums)
if l <= 1:
return 0 if l==0 else nums[0]
else:
#递归计算左半边最大子序和
max_left = self.maxSubArray(nums[0:l//2])
#递归计算右半边最大子序和
max_right = self.maxSubArray(nums[l//2:l])
#计算中间的最大子序和,从右到左计算左边的最大子序和,从左到右计算右边的最大子序和,再相加
max_l = nums[l//2 -1]
tmp = 0
for i in range(l//2 -1,-1,-1):
tmp += nums[i]
max_l = max(tmp, max_l)
max_r = nums[l//2]
tmp = 0
for i in range(l//2,l):
tmp += nums[i]
max_r = max(tmp, max_r)
#返回三个中的最大值
return max(max_right,max_left,max_l+max_r)
分析:
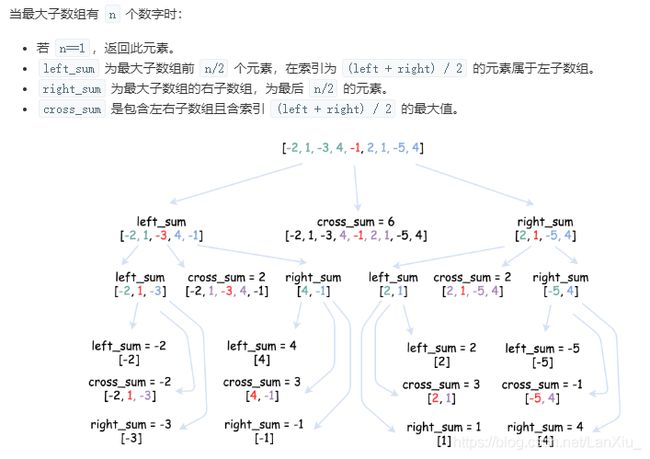
官方说分治法更为精美,其实…,这道题里分治法比动态规划效率低。代码中有一些注释,下面有一张图详细举例了这道题分治的过程。
复杂度:
时间复杂度: O(N*logN)
空间复杂度: O(1)
No.54.螺旋矩阵
题解代码(Python3.8)
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix:
return []
L_row = len(matrix)
L_col = len(matrix[0])
def spiral(depth):
l_row,l_col = L_row-2*depth,L_col-2*depth
if l_row<=0 or l_col<=0:
return []
if l_row==1:
return matrix[depth][depth:depth+l_col]
if l_col==1:
return [ matrix[i][depth] for i in range(depth,depth+l_row) ]
res = []
res += matrix[depth][depth:depth+l_col]
res += [ matrix[i][depth+l_col-1] for i in range(depth+1,depth+l_row-1) ]
res += reversed(matrix[depth+l_row-1][depth:depth+l_col])
res += reversed([ matrix[i][depth] for i in range(depth+1,depth+l_row-1) ])
return res + spiral(depth+1)
return spiral(0)
或许有用的知识点:
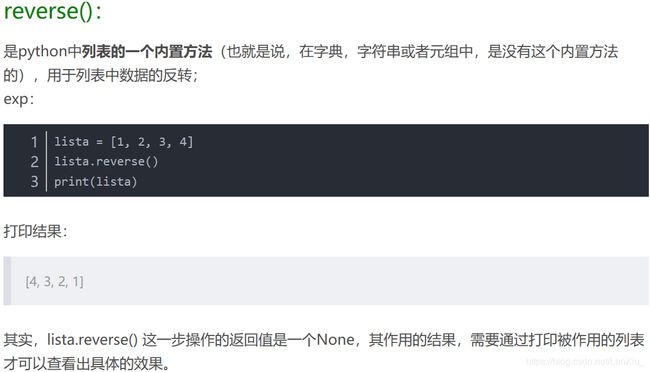
可以了解一下Python中的reverse()函数和reversed(),一般用于反转python中大多类型的数据,下面是这两个函数的一些介绍:

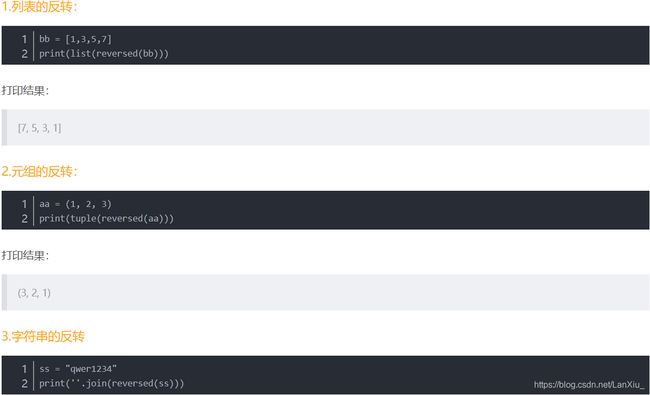
解题思路:
设置一个空列表res,定义一个递归函数spiral,从外到内一层一层记录二维数组的值并递归到下一层即可,最后输出res,代码非常好理解。
No.55.跳跃游戏
题解代码(Python3.8)
class Solution:
def canJump(self, nums: List[int]) -> bool:
max_jump=0
l=len(nums)
for i in range(l):
max_jump = max(max_jump,i+nums[i])
if max_jump>=l-1:
return True
if max_jump<i+1:
break
return False
或许有用的知识点:
这道题可以用到贪心算法。
解题思路:
总思路:如果最大跳跃距离大于等于最后一个位置的索引,就表示能够到达最后一个位置,反之则不能。
贪心算法:
定义能达到的最远位置max_jump=0,遍历数组,遍历范围[0,n-1);
所能达到的最远位置max_jump=max(max_jump,nums[i]+i),表示上一最远位置和当前索引i和索引i上的步数之和中的较大者。
如果max_jump大于等于最后一个位置的索引,就return True。
注意:数组遍历范围为[0,n-1)。
复杂度分析
时间复杂度:O(n)
空间复杂度:O(1)
其实这道题和‘No.45.跳跃游戏Ⅱ’思路很相似,‘No.45.跳跃游戏Ⅱ’是这道题的升级版,大家可以做一下这道题练习一下。
No.45.跳跃游戏Ⅱ:
https://blog.csdn.net/LanXiu_/article/details/104177349