(十)论文阅读 | 目标检测之Cascade R-CNN
文章目录
- 简介
- 0. Abstract
- 1. Introduction
- 2. Related Work
- 3. Object Detection
- 3.1 Bounding Box Regression
- 3.2 Detection Quality
- 4. Cascade R-CNN
- 4.1 Cascaded Bounding Box Regression
- 4.2 Cascaded Detection
- 5. Experimental Results
- 6.Conclusion
- 参考
简介
论文是发表在 C V P R 2018 {\rm CVPR\ 2018} CVPR 2018上的一篇关于目标检测的论文, C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN是一个多阶段监测器,通过设置不同的 I o U {\rm IoU} IoU值级联几个检测网络达到不断优化检测结果的目的。
论文原文 源码
0. Abstract
在目标检测中,通常使用 I o U {\rm IoU} IoU确定正负样本。随着 I o U {\rm IoU} IoU阈值的增大,模型性能往往会下降:(1)阈值增大意味着更少的正样本,容易导致模型过拟合;(2)训练模型与推理使用不同 I o U {\rm IoU} IoU值会出现不匹配现象(在训练阶段可以通过 I o U {\rm IoU} IoU阈值区别正负样本,得到的正样本质量更高;而推理阶段由于没有标注框,将所有得到的结果当做正样本,所以得到的正样本质量不如前者。下面实验有证明这个问题)。作者提出 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN用于解决上述问题,它由一组使用逐渐增加的 I o U {\rm IoU} IoU值所训练的检测器组成,避免产生密集的假阳性结果。基于当前模型输出可以作为下一个模型的有效输入, C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN通过一个阶段接着一个阶段的方式训练。这种再采样的方法有效地减弱了模型的过拟合(当前模型的输出是经过修正后的结果,得到更多高质量的候选框,这样提高 I o U {\rm IoU} IoU值也能获得足够的正样本)。在推理阶段也使用这种级联的结构,使得假设和模型更加匹配。实验结果为在 M S C O C O {\rm MS\ COCO} MS COCO数据集上达到了 S O T A {\rm SOTA} SOTA。
论文贡献:(一)提出一种多阶段级联的目标检测算法;(二)级联思想可以应用到其他检测算法中;(三)给出了一种在目标检测中 I o U {\rm IoU} IoU选取的策略。
1. Introduction
在基于 R {\rm R} R- C N N {\rm CNN} CNN的两阶段检测算法中, I o U {\rm IoU} IoU阈值通常设置为 0.5 0.5 0.5,但得到的正样本质量不高。如下图:
如图 ( a ) {\rm (a)} (a)和 ( b ) {\rm (b)} (b)是由不同 I o U {\rm IoU} IoU值得到结果, u = 0.7 u=0.7 u=0.7的结果要好于 u = 0.5 u=0.5 u=0.5。图 ( c ) {\rm (c)} (c)横轴表示对 R P N {\rm RPN} RPN所使用的阈值,纵轴表示经回归后得到的边界框同标注框的 I o U {\rm IoU} IoU值,而不同颜色的线表示使用不同阈值训练模型。实验结果表明,当 R P N {\rm RPN} RPN所用阈值与模型训练所使用的阈值较接近时,得到的结果更好。如蓝色的线 u = 0.5 u=0.5 u=0.5在横坐标为 0.5 0.5 0.5附近时得到的结果最好。这就证明了摘要部分提到的不匹配问题。图 ( d ) {\rm (d)} (d)是采用不同 I o U {\rm IoU} IoU值训练模型所得到的 A P {\rm AP} AP值,验证了简单地增加 I o U {\rm IoU} IoU值不能提高模型的性能。
由此,作者提出了 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN,它是一种序列化模型,当前模型的输出作为下一个模型的输入。由上图 ( c ) {\rm (c)} (c)可知,由不同 I o U {\rm IoU} IoU训练得到的模型结果大都位于灰线以上,这表明可使用特定 I o U {\rm IoU} IoU值训练模型的输出可以作为更高 I o U {\rm IoU} IoU值训练模型的输入。(单一阈值训练的模型性能有限,如果采用 0.5 0.5 0.5训练的模型,得到的 I o U {\rm IoU} IoU在 0.5 0.5 0.5附近;而加如增大 I o U {\rm IoU} IoU阈值会得到如图 ( d ) {\rm (d)} (d)的结果。而现在采用一组逐渐增大的 I o U {\rm IoU} IoU 0.5 0.5 0.5、 0.6 0.6 0.6、 0.7 0.7 0.7训练模型。如使用 0.5 0.5 0.5得到的 I o U {\rm IoU} IoU为 0.55 0.55 0.55,经过 0.6 0.6 0.6得到的 I o U {\rm IoU} IoU为 0.65 0.65 0.65,经过 0.6 0.6 0.6得到的 I o U {\rm IoU} IoU为 0.75 0.75 0.75…)因此,每个阶段的过程是致力于得到有效的样本用于训练下一个阶段。在推理阶段也采取同样的操作。
C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN是一个简单高效的模型,可以集成到任何基于 R {\rm R} R- C N N {\rm CNN} CNN的两阶段检测算法中。
2. Related Work
相关工作部分首先介绍了基于 R {\rm R} R- C N N {\rm CNN} CNN的检测算法,以及 Y O L O {\rm YOLO} YOLO、 S S D {\rm SSD} SSD、 R e t i n a N e t {\rm RetinaNet} RetinaNet等一阶段检测算法。最后谈及了基于迭代边界框回归的多阶段检测算法。
3. Object Detection
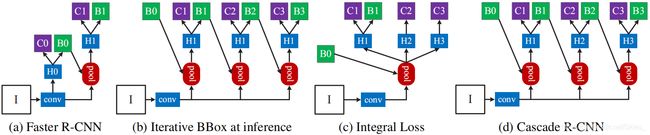
图 ( a ) {\rm (a)} (a)是 F a s t e r R {\rm Faster\ R} Faster R- C N N {\rm CNN} CNN结构,其中“H0”为产生建议框的过程 R P N {\rm RPN} RPN,“H0”为产生的建议框,“H1”为检测头、后接分类分支和回归分支,“C”和“B”分别为分类分支和回归分支。(下同)对比图 ( b ) {\rm (b)} (b)和 ( d ) {\rm (d)} (d),迭代边界框回归采用同 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN类似的级联结构,但是每次使用的 I o U {\rm IoU} IoU阈值相同,即共用检测头“H1”。而图 ( c ) {\rm (c)} (c)使用了不同的检测头,但是不是级联的结构,只是将不同的检测结果融合。
3.1 Bounding Box Regression
令建议框为 b = ( b x , b y , b w , b h ) {\rm b}=(b_x,b_y,b_w,b_h) b=(bx,by,bw,bh)、标注框为 g {\rm g} g,边界框回归的目的是找到一种映射 f f f使得 f ( b ) = g f({\rm b})={\rm g} f(b)=g。为了控制回归过程中尺度和位置变化,一般采用向量 Δ = ( δ x , δ y , δ w , δ h ) Δ=(δ_x,δ_y,δ_w,δ_h) Δ=(δx,δy,δw,δh)作为预测值: δ x = ( g x − b x ) / b w , δ y = ( g y − b y ) / b h δ w = l o g ( g w / b w ) , δ h = l o g ( g h / b h ) (3.1) δ_x=(g_x-b_x)/b_w,\ δ_y=(g_y-b_y)/b_h\\ δ_w={\rm log}(g_w/b_w),\ δ_h={\rm log}(g_h/b_h)\tag{3.1} δx=(gx−bx)/bw, δy=(gy−by)/bhδw=log(gw/bw), δh=log(gh/bh)(3.1)
由于在回归过程中,每次只对 b b b作微小的调整, Δ Δ Δ往往非常小。所以回归损失函数通常小于分类损失。为了提高回归效率,通常会对上式变形,如使用 δ x ′ = ( δ x − μ x ) / σ x δ_x^{'}=(δ_x-μ_x)/σ_x δx′=(δx−μx)/σx代替 δ x δ_x δx。
此外,前人已有工作证明了单次回归不足以训练高性能的模型。转而使用迭代式的回归方法,如图 3 3 3中的 ( b ) {\rm (b)} (b): f ′ ( x , b ) = f ○ f ○ … ○ f ( x , b ) (3.2) f^{'}(x,{\rm b})=f○f○…○f(x,{\rm b})\tag{3.2} f′(x,b)=f○f○…○f(x,b)(3.2)
但是,这种结构也存在以下问题:(1)单个阈值如 u = 0.5 u=0.5 u=0.5并不能得到最佳模型,如图 3 3 3中的 ( c ) {\rm (c)} (c);(2)在每次迭代后,边界框的偏移变化剧烈。如下图:
图中横纵坐标是上述提到的 Δ Δ Δ值,其中图中红色点属于离群点,大量噪声不利于网络的训练。由上图可知,经过每次的迭代,虽然得到的值更加集中(边界框更接近于标注框),但也产生了大量的离群点。这会给下次模型的带来大量的噪声,不利于模型的训练。
3.2 Detection Quality
分类器 h ( x ) h(x) h(x)给图像 x x x分配类别,给定一个训练样本 ( x i , y i ) (x_i,y_i) (xi,yi),目的是最小化一个分类交叉熵损失函数 L c l s ( h ( x i , y i ) ) L_{cls}(h(x_i,y_i)) Lcls(h(xi,yi))。通常使用 I o U {\rm IoU} IoU 值为建议框预分配类别标签。则根据阈值 u u u和类别 g y g_y gy,有:
y = { g y , I o U ( x , g ) ≥ u 0 , o t h e r w i s e (3.3) y=\left\{ \begin{aligned} &g_y,&IoU(x,g)≥u\\ &0,&otherwise\\ \end{aligned} \right.\tag{3.3} y={gy,0,IoU(x,g)≥uotherwise(3.3)
这里阈值 u u u的设置成为关键,如果 u u u太大,不能得到足够多的正样本;如果 u u u太小,在正样本中包含很多负样本。一种解决的方法如图 3 3 3中的 ( c ) {\rm (c)} (c),则分类损失函数定义为: L c l s ( h ( x ) , y ) = ∑ u ∈ U L c l s ( h u ( x ) , y u ) (3.4) L_{cls}(h(x),y)=\sum_{u∈U}L_{cls}(h_u(x),y_u)\tag{3.4} Lcls(h(x),y)=u∈U∑Lcls(hu(x),yu)(3.4)
如上图中的纵轴为正样本数。如第一幅图所示,正样本数随着 I o U {\rm IoU} IoU值增大而急剧减小,这将导致模型的过拟合。此外,分类器既要处理高质量的正样本,也要处理低质量的正样本,这将导致其不能很好地优化。由此证明上式 ( 3.4 ) (3.4) (3.4)不能很好地应对 I o U {\rm IoU} IoU值的变化。后两幅图是 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN处理的结果。
4. Cascade R-CNN
4.1 Cascaded Bounding Box Regression
在 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN中,模型以级联的方式构建,如图 3 3 3中的 ( d ) {\rm (d)} (d): f ( x , b ) = f T ○ f T − 1 … ○ f 1 ( x , b ) (4.1) f(x,{\rm b})=f_T○f_{T-1}…○f_1(x,{\rm b})\tag{4.1} f(x,b)=fT○fT−1…○f1(x,b)(4.1)
作者指出,与迭代式的边界框回归不同的是(如图 3 3 3中的 ( b ) {\rm (b)} (b)), C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN是一个再采样的过程,每个阶段输入的分布都不相同;在训练和推理阶段使用相同的分布;在每个阶段使用再采样样本对回归模型 { f T , f T − 1 , … f 1 } \{f_T,f_{T-1},…f_1\} {fT,fT−1,…f1}优化。
4.2 Cascaded Detection
如图 3 3 3中的 ( d ) {\rm (d)} (d), C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN的每个阶段通过阈值 u t u^t ut优化分类器 h t h_t ht和回归器 f t f_t ft,且 u t > u t − 1 u^t>u^{t-1} ut>ut−1。通过最小化以下损失函数优化分类器和回归器: L ( x t , g ) = L c l s ( h t ( x t ) , y t ) + λ [ y t ≥ 1 ] + L l o c ( f t ( x t , b t ) , g ) (4.2) L(x^t,g)=L_{cls}(h_t(x^t),y^t)+λ[y^t≥1]+L_{loc}(f_t(x^t,{\rm b}^t),{\rm g})\tag{4.2} L(xt,g)=Lcls(ht(xt),yt)+λ[yt≥1]+Lloc(ft(xt,bt),g)(4.2)
这里 b t = f t − 1 ( x t − 1 , b t − 1 ) {\rm b}^t=f_{t-1}(x^{t-1},{\rm b}^{t-1}) bt=ft−1(xt−1,bt−1), g g g是对于 x t x^t xt的标注框, λ = 1 λ=1 λ=1,[·]为指示函数, y t y^t yt是在给定阈值 u t u^t ut下 x t x^t xt的类别标签。由上式可知,当前阶段的位置预测损失函数同前一阶段相关,通过结构的级联得到损失函数的级联。
5. Experimental Results
如图 3 3 3中的 ( d ) {\rm (d)} (d)为 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN的结构,共采用 3 3 3个阶段,阈值分别设置为 0.5 0.5 0.5、 0.6 0.6 0.6、 0.7 0.7 0.7。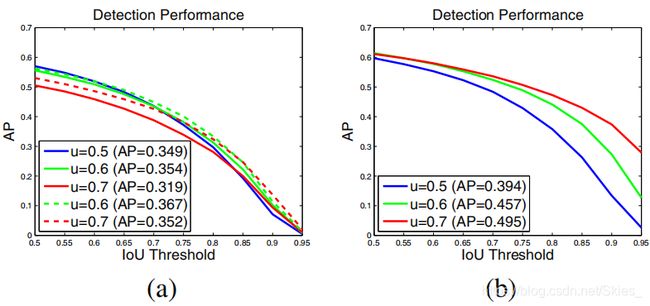
上图 ( a ) {\rm (a)} (a)中实线为单个检测器的结果,阈值分别设置为 0.5 0.5 0.5、 0.6 0.6 0.6、 0.7 0.7 0.7。虚线是 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN加入级联后得到的 A P {\rm AP} AP值。 ( b ) {\rm (b)} (b)中为加入标注框后的实验结果。横纵为设置的 I o U {\rm IoU} IoU值,纵轴为 A P {\rm AP} AP值,各实线为相应 I o U {\rm IoU} IoU值训练的检测器。三者均有提升,但阈值为 0.7 0.7 0.7的模型提升最明显。
由上组实验得到的结论为: u = 0.5 u=0.5 u=0.5并非最佳的阈值;通过高阈值的训练才能得到高精度的检测器。
如图为 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN同 I t e r a t i v e B B o x {\rm Iterative\ BBox} Iterative BBox和 I n t e g r a l L o s s {\rm Integral\ Loss} Integral Loss的对比:
此外,论文还有针对 I o U {\rm IoU} IoU值选取、阶段数、回归策略等做了消融实验。详细步骤及结果请查看原文。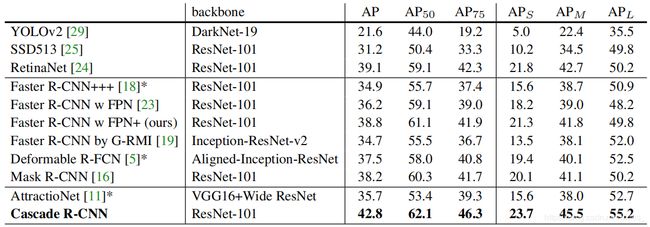
由上图可以得到,在两阶段算法中加入级联结构后,在不显著增大计算量和参数的情况下提高了模型的精度。
6.Conclusion
论文提出的 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN是一种多阶段的目标检测方法。平衡了提高 I o U {\rm IoU} IoU阈值对提高检测性能的利弊。一方面,提高 I o U {\rm IoU} IoU阈值可以得到高质量的正样本,从而提高检测器的性能;另一方面,提高 I o U {\rm IoU} IoU阈值显著减少了正样本的数量,增加了模型过拟合的风险。 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN的级联思想可以应用于其他检测算法中,进一步提高模型性能。
由于没有阅读源码,本文只总结了 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN的大体结构和信息,详细内容请阅读论文原文。
参考
- Cai Z, Vasconcelos N. Cascade R-CNN: Delving Into High Quality Object Detection[C]. computer vision and pattern recognition, 2018: 6154-6162.
- https://blog.csdn.net/qq_21949357/article/details/80046867.
- https://zhuanlan.zhihu.com/p/42553957.