python数据结构(二)

第二章–算法

目录

---

1. 数据结构与算法
2. 算法定义
3. 算法特性
4. 算法设计的要求
5. 算法效率的度量方法
6. 函数渐近增长
7. 算法时间复杂度

---

1. 数据结构与算法关系

1.数据结构是底层，算法高层
2.数据结构为算法提供服务；
3.算法围绕数据结构操作；
二者之间是密不可分的。但在数据结构的书中，通常谈到算法也是为了更好的帮助理解数据结构 。

就像太极图一样

2.算法定义

算法是解决特定问题解求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令指示一个或多个操作。
从定义我们可以看出没有“包治百病”的算法。

3.算法特性

五个基本特性：

• 输入
• 输出
• 有穷性 — 即在可接受的时间内完成
• 确定性 — 即算法的每一步必须有确定的含义，不能有二义性
• 可行性 — 即可以通过有限次数完成

4.算法设计的要求

• 正确性
• 可读性
• 健壮性 — 即当输入不合法的数据时，算法也能做出相关处理，不出现异常
• 存储低
• 时间效率高

5.算法设计的要求

我们提到设计算法要提高效率。 这里效率大都指算法的执行时间。 那么我们如何度量一个算法的执行时间呢?

事前统计方法：这种方法主要是通过设计好的测试程序和数据，利用计算机计时器对不同算法编制的程序的运行时间进行比较，从而确算法效率的高低。

这种方法有很大缺陷： 如果测试完了，发现算法效率低，“竹篮打水一场空”，同时该方法对于时间的比较，依赖硬软件等因素，有时会掩盖算法本身的优势，数据的测试比较困难，比如效率高的算法可能在小数据上体现不出来。

事后统计方法：最可靠的方法就是计算对运行时间有消耗的基本操作的执行次数， 而运行时间与这个计数成正比。
我们举例进行比较，比如计算从1到100的和：

#1.第一种方法
sum=0 ，n=100                    #执行一次
for i in range(1,n+1):			 #执行n次
	sum = sum + i				 #执行n次
print(sum)					     #执行1次

#第二种方法
sum=0 ,n=100                     #执行一次
sum=(1+n)*n/2					 #执行一次
print(n)						 #执行一次

显然，第一种执行了2n+2次，第二种执行3次，通常我们只关注中间循环部分，将循环看作一个整体，就是n次与1次的比较。
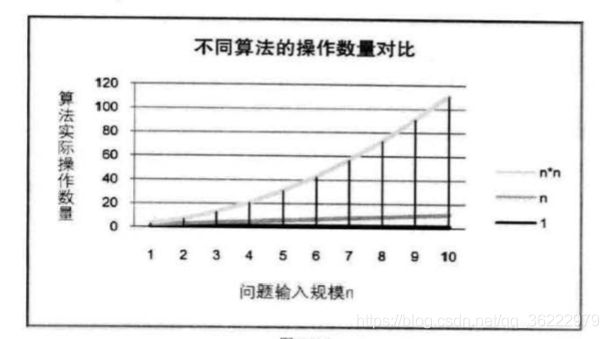
以上两个，都是输入个数都是n=100，通常把执行次数看作输入的函数F(n),在分析一个算法的运行时间时，重要的是把基本操作的数量与输入规模关联起来,基本操作的数量必须表示成输入规模的函数，然后观察随着n的变化，F(n)的变化来判断最好的算法，也就是下文所提的函数渐进增长。

6. 函数渐进增长

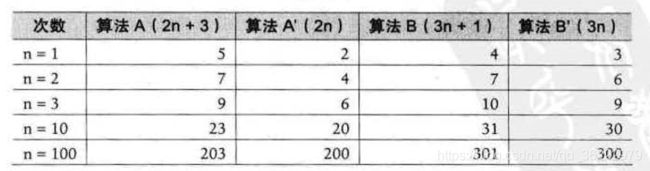
假设两个算法的输入规模都是 n，算法 A 要做 2n + 3 次操作，你可以理解为先有一个 n 次的循环，执行完成后，再有一次n次循环，最后有三次循环，共 2n + 3 次操作。 算法 B 要做 3n + 1 次 操作。你觉得它们谁更快呢?
准确说来，答案是不一定的

7. 算法时间复杂度

通过前面两节一系列的概念，最终引出本节，利用算法复杂度来表示算法的性能。
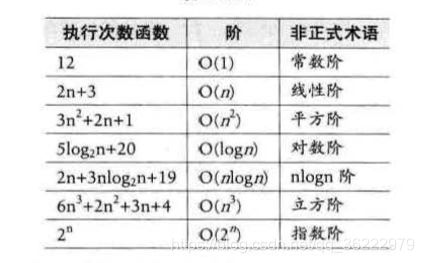
定义：在进行算法分析时， 语句总的执行次数 T ( n )是关于问题规模n的函数，进而分析 T ( n )随 n 的变化情况并确定T(n)的数量级。算法的时间复杂度.也就是算法的时间量度，记作: T ( n ) = O(f(n))。 它表示随着间间规模 n 的增大，算法执行时间的增长率和 f(n)的增长率相同，叫做算法的渐近时间复杂度，简称为时间复杂度。 其f(n)是问题规模 n 的某个函数。这种方法我们称之为大O记法。也就是在函数F(n)渐进增长的基础上，使用大O记法罢了，而没有直接用函数的渐进增长来表示复杂度。
这样， 之前两个例子的时间复杂度分别为:O(1) ,O(n) 。，如此类推，还有O(n^2)等复杂度。

推导大 O 阶方法

常见的阶数有：

除此外，还有空间复杂度，但通常复杂度指的是时间复杂度！