第11章 散列表
11.1 直接寻址表
11.1-1
假设一动态集合S用一个长度为m的直接寻址表T来表示。给出一个查找S中最大元素的过程。
DIRECT-ADDRESS-MAXIMUM(T)
max = -∞
for i = 1 to m
if T[i] ≠ NIL and T[i].key > max
max = T[i].key
j = i
return T[j]过程在最坏情况下的运行时间是![]() 。
。
11.1-2
用一个位向量来表示一个包含不同元素(无卫星数据)的动态集合。字典操作的运行时间应为![]() 。
。
DIRECT-ADDRESS-SEARCH(T, k)
if T[k] == 0
return NIL
else return k
DIRECT-ADDRESS-INSERT(T, k)
T[k] = 1
DIRECT-ADDRESS-DELETE(T, k)
T[k] = 011.1-3
实现一个直接寻址表,表中各元素的关键字不必都不相同,且各元素可以有卫星数据。所有三种字典操作(INSERT、DELETE和SEARCH)的运行时间为![]() 。(DELETE要处理的是被删除对象的指针变量,而不是关键字。)
。(DELETE要处理的是被删除对象的指针变量,而不是关键字。)
DIRECT-ADDRESS-SEARCH(T, k)
return T[k]
DIRECT-ADDRESS-INSERT(T, x)
x.next = T[x.key]
T[x.key] = x
DIRECT-ADDRESS-DELETE(T, x)
a = T[x.key]
b = NIL
while a ≠ x
b = a
a = a.next
if b == NIL
T[x.key] = x.next
else b.next = x.next11.2 散列表
11.2-1
对关键字k和l,定义指示器随机变量![]() 。在简单均匀散列的假设下,有
。在简单均匀散列的假设下,有![]() ,从而根据引理5.1,有
,从而根据引理5.1,有![]() 。于是,集合{{k,l}:k≠l,且h(k)=h(l)}基的期望值是
。于是,集合{{k,l}:k≠l,且h(k)=h(l)}基的期望值是![E[X]=\sum _{k=1}^{n}{\sum _{l=k+1}^{n}{\frac{1}{m}}}=\sum _{k=1}^{n}{\frac{n-k}{m}}=\frac{n(n-1)}{m}](http://img.e-com-net.com/image/info8/15210f0896bd4c8097d9aa7f3fc72d80.gif) 。
。
11.2-2
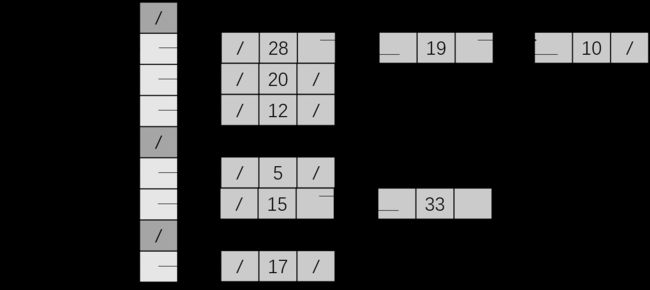
对于一个用链接法解决冲突的散列表,说明将关键字5,28,19,15,20,33,12,17,10插入到该表中的过程。设该表中有9个槽位,并设其散列函数为![]() 。
。
11.2-3
Marley教授的改动对成功查找、不成功查找、插入和删除操作的运行时间的影响:
- 成功查找操作的运行时间仍然为
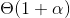 。
。 - 不成功查找操作的运行时间是改动前的一半,但仍然为
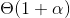 。
。 - 插入操作的运行时间由
 变成
变成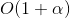 。
。 - 删除操作的运行时间仍然为
 。
。
11.2-4
该空闲链表需要是双链表。
CHAINED-HASH-ALLOCATE(T, k)
T[k].flag = 1
if T[k].prev ≠ NIL
T[k].prev.next = T[k].next
else T.free = T[k].next
if T[k].next ≠ NIL
T[k].next.prev = T[k].prev
CHAINED-HASH-DEALLOCATE(T, k)
T[k].flag = 0
if T.free ≠ NIL
T[k].prev = T.free.prev
T.free.prev = T[k]
T[k].next = T.free
T.free = T[k]
CHAINED-HASH-INSERT(T, x)
if T[h(x.key)].flag == 0
CHAINED-HASH-ALLOCATE(T, h(x.key))
T[h(x.key)] = x
else insert x at the head of list T[h(x.key)]
CHAINED-HASH-SEARCH(T, k)
if T[h(x.key)].flag == 0
return NIL
else search for an element with key k in list T[h(k)]
CHAINED-HASH-DELETE(T, x)
if x.prev == NIL and x.next == NIL
CHAINED-HASH-DEALLOCATE(T, h(x.key))
else if x.prev != NIL and x.next == NIL
x.prev.next = x.next
else if x.prev == NIL and x.next != NIL
T[h(x.key)] = x.next
x.next.prev = x.prev
else delete x from the list T[h(x.key)]11.2-5
证明:因为![]() ,所以当将全域U中的所有关键字存储到一个大小为m的散列表中时,每个槽位中至少有n个关键字。因此,U中有一个大小为n的子集,其由散列到同一槽位中的所有关键字构成,使得链接法散列的查找时间最坏情况下为
,所以当将全域U中的所有关键字存储到一个大小为m的散列表中时,每个槽位中至少有n个关键字。因此,U中有一个大小为n的子集,其由散列到同一槽位中的所有关键字构成,使得链接法散列的查找时间最坏情况下为![]() 。
。
11.2-6
因为![]() ,最长链的长度为L,所以
,最长链的长度为L,所以![]() 。根据定理11.2,从散列表的所有关键字中均匀随机地选择某一元素并返回该关键字的期望时间为
。根据定理11.2,从散列表的所有关键字中均匀随机地选择某一元素并返回该关键字的期望时间为![]() ,也即
,也即![]() 。
。
11.3 散列函数
11.3.1 除法散列法
11.3.2 乘法散列法
11.3-1
在表中查找具有给定关键字的元素时,先计算给定关键字的散列值,然后将该散列值与链表中每一个元素的散列值进行比较,相等的即是要找的元素。
11.3-2
设字符串表示成以128为基数的数为![]() ,则
,则![]() 。
。
11.3-3
证明:设字符串x表示成以![]() 为基数的数为
为基数的数为![]() ,根据上一题的结果,
,根据上一题的结果,![]() ,所以字符串x的散列值与其字符的排列顺序无关。因此,如果串x可由串y通过其自身的字符置换排列导出,则x和y具有相同的散列值。
,所以字符串x的散列值与其字符的排列顺序无关。因此,如果串x可由串y通过其自身的字符置换排列导出,则x和y具有相同的散列值。
11.3-4
h(61)=700,h(62)=318,h(63)=936,h(64)=554,h(65)=172。
11.4 开放寻址法
11.4-1
用开放寻址法将关键字10、22、31、4、15、28、17、88、59插入到一长度为m=11的散列表中,辅助散列函数为![]() 。说明分别用线性探查、二次探查
。说明分别用线性探查、二次探查![]() 和双重散列
和双重散列![]() 将这些关键字插入散列表的过程。
将这些关键字插入散列表的过程。
11.4-2
写出HASH-DELETE的伪代码;修改HASH-INSERT,使之能处理特殊值DELETED。
HASH-DELETE(T, k)
for i = 0 to m-1
j = h(k, i)
if T[j] == k
T[j] = DELETED
return
HASH-INSERT(T, k)
i = 0
repeat
j = h(k, i)
if T[j] == NIL or T[j] == DELETED
T[j] = k
return j
else i = i + 1
until i == m
error "hash table overflow"11.4-3
当装载因子为3/4和7/8时,根据定理11.6,一次不成功查找的探查期望数上界分别为4和8,根据定理11.8,一次成功查找的探查期望数上界分别为![]() 和
和![]() 。
。
思考题
11-1 散列最长探查的界
a.证明:设第i次插入需要![]() 次探查,易得:
次探查,易得:![]() 。因为
。因为![]() ,所以
,所以![]() 。因此,对于i=1,2,...,n,第i次插入需要严格多于k次探查的概率至多为
。因此,对于i=1,2,...,n,第i次插入需要严格多于k次探查的概率至多为![]() 。
。
b.证明:根据第a小问的结论,对于i=1,2,...,n,第i次插入需要多于![]() 次探查的概率至多为
次探查的概率至多为![]() ,也即
,也即![]() 。
。
c.证明:根据第b小问的结论,![]() 。因此,
。因此,![]() 。
。
11-2 链接法中槽大小的界
a.证明:
因此,正好有k个关键字被散列到某一特定槽中的概率![]() 为
为![]() 。
。
b.证明:设随机变量![]() 表示第i个槽中所含关键字数,
表示第i个槽中所含关键字数,![]() 表示第i个槽中有k个关键字。根据第a小问的结论,
表示第i个槽中有k个关键字。根据第a小问的结论,![]() 。因此,
。因此,![]()
![]() 。
。
d.证明:为证![]() 对
对![]() 成立,只需证
成立,只需证![]() ,两边取对数得到:
,两边取对数得到:![]()
![]()
![]() ,令c>e得:
,令c>e得:![]() 。令
。令![]() 得:
得:![]() ,所以
,所以![]() 。因此,当c>6时,
。因此,当c>6时,![]() 对
对![]() 成立。
成立。
根据第b小问的结论,![]() 。
。
11-3 二次探查
a.当![]() 时,可得该方案是一般的“二次探查”法的一个实例。
时,可得该方案是一般的“二次探查”法的一个实例。
b.证明:因为二次探查确实能够检查表中的每一个位置,所以在最坏情况下,这个算法要检查表中的每一个位置。
11-4 散列和认证
a.证明:因为散列函数簇![]() 是2全域的,所以如果对每个由2个不同的关键字
是2全域的,所以如果对每个由2个不同的关键字![]() 构成的固定序列,以及从
构成的固定序列,以及从![]() 中随机选出的任意散列函数h,序列
中随机选出的任意散列函数h,序列![]() 是
是![]() 个长度为2的序列(其元素取自{0,1,...,m-1})中任意一个的可能性相同。所以,对任意两个不同的关键字
个长度为2的序列(其元素取自{0,1,...,m-1})中任意一个的可能性相同。所以,对任意两个不同的关键字![]() ,
, ,也即发生碰撞的概率是1/m。因此,如果散列函数簇
,也即发生碰撞的概率是1/m。因此,如果散列函数簇![]() 是2全域的,则它是全域的。
是2全域的,则它是全域的。
b.证明:因为散列结果有p种可能,所以发生碰撞的概率为1/p,因此,![]() 是全域的。考虑元素
是全域的。考虑元素![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,所以
,所以![]() 与以0开头的p个序列的散列值都相同,但与剩下的
与以0开头的p个序列的散列值都相同,但与剩下的![]() 个序列的散列值不相同,因此,
个序列的散列值不相同,因此,![]() 不是2全域的。
不是2全域的。
c.证明:考虑固定的n元组![]() 和
和![]() ,因为
,因为![]() 和
和![]() 包括
包括![]() ,对于任意的序列a,b能取0~p-1中的任意一个数,所以
,对于任意的序列a,b能取0~p-1中的任意一个数,所以![]() 等可能取0~p-1中的某一个数,所以
等可能取0~p-1中的某一个数,所以![]() 是
是![]() 个长度为2的序列中任意一个的可能性相同。因此,
个长度为2的序列中任意一个的可能性相同。因此,![]() 是2全域的。
是2全域的。
d.证明:因为散列函数簇![]() 是2全域的,所以任取
是2全域的,所以任取![]() 中的一个散列函数,对于某个
中的一个散列函数,对于某个![]() ,
,![]() 总共有p种可能。因为对手不知道Alice和Bob约定的散列函数h是哪个,所以他成功地欺骗Bob接受
总共有p种可能。因为对手不知道Alice和Bob约定的散列函数h是哪个,所以他成功地欺骗Bob接受![]() 的概率至多为1/p,即使他知道所用的散列函数簇
的概率至多为1/p,即使他知道所用的散列函数簇![]() 。
。

![E[X]=\sum _{X_{i}=1}^{n}{X_{i}P\{X=X_{i}\}}=\sum _{X_{i}=1}^{2\lg{n}}{X_{i}P\{X=X_{i}\}}+\sum _{X_{i}=2\lg{n}+1}^{n}{X_{i}P\{X=X_{i}\}}](http://img.e-com-net.com/image/info8/23908ad683fc4511ad6fdd54a4855634.gif)
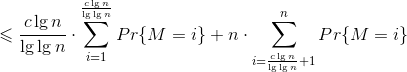
![E[M]=Pr\{M\leqslant \frac{c\lg{n}}{\lg{\lg{n}}}\}\cdot \frac{c\lg{n}}{\lg{\lg{n}}}+n\cdot \sum _{i=\frac{c\lg{n}}{\lg{\lg{n}}}+1}^{n}{Pr\{M=i\}}](http://img.e-com-net.com/image/info8/7a2e7271fca84cdaa46e30a9eb17aa21.gif)