《统计思维：程序员数学之概率统计》学习笔记 Chap.1-2

最近在阅读Allen B. Downey所著的《统计思维：程序员数学之概率统计》，由于文章中大部分的函数操作都是基于作者自己写的模块thinkstats2，为了能够使用常用python库来复现操作，加深自己对文章内容的理解，故记录此读书笔记。

前期准备

首先导入数据分析三件套

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

之后为了导入文章所用数据，需要使用sys模块，再把数据文件所在的路径复制到sys.path列表当中。

import sys
sys.path.append('E:\\Anaconda\\Lib\\ThinkStats2-master\\code')

再传入数据，nsfg文件中的ReadFemPreg函数会返回一个描述美国新生儿数据的DataFrame，用作之后的分析。

import nsfg
df = nsfg.ReadFemPreg(dct_file='E:\\Anaconda\\Lib\\ThinkStats2-master\\code\\2002FemPreg.dct', dat_file='E:\\Anaconda\\Lib\\ThinkStats2-master\\code\\2002FemPreg.dat.gz')

绘制直方图

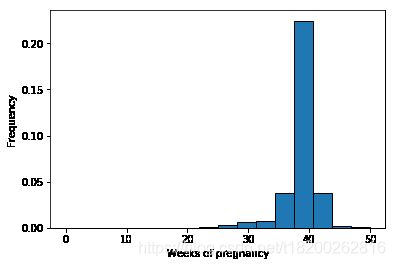
直方图的绘制主要用到plt模块中的hist函数。当绘制产妇怀孕数据的直方图时，发现与书上结果不同。检查后发现需要添加成功怀孕（即outcome=1）的条件。代码如下：

# 找出成功生育的产妇，并去除空值
weeks = df.prglngth[df['outcome']==1].dropna() 
# bins指定直方个数，density指定是否将纵坐标归一化，edgecolor指定边框颜色
hist = plt.hist(weeks, bins=16, density=True, edgecolor='black')
plt.xlabel('Weeks of pregnancy') # x轴命名
plt.ylabel('Frequency') # y轴命名

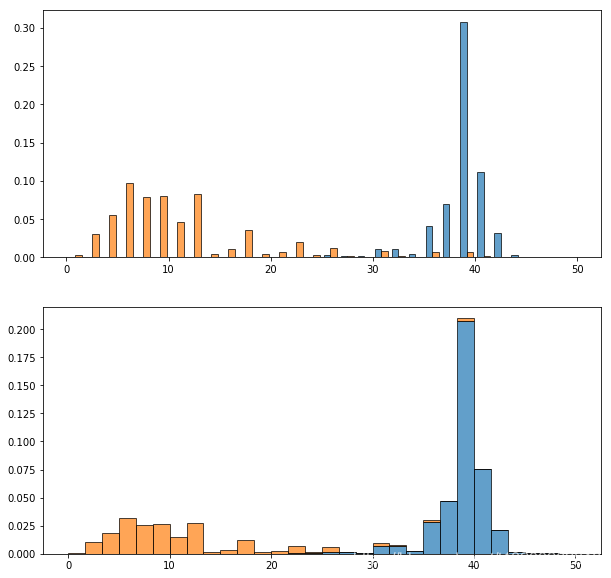
另外，通过设置直方图的 histtype 参数，可以实现用不同方式将两类数据组合在一张图中。我分别选取了成功生育和未成功生育的产妇的怀孕周数数据，并通过在两个子图中分别设置 histtype 参数为 bar 或 barstacked，来直观地体现出两者的差距。

plt.figure(figsize=[10,10]) 
ax1 = plt.subplot(2, 1, 1) # 初始化子图1
ax2 = plt.subplot(2, 1, 2) # 初始化子图2
weeks_live = df.prglngth[df['outcome']==1].dropna() # 成功生育产妇数据
weeks_all = df.prglngth[df['outcome']!=1].dropna() # 未成功生育产妇数据
hist = ax1.hist([weeks_live, weeks_all], bins=30, density=True, edgecolor='black', alpha=0.7, histtype='bar')
hist = ax2.hist([weeks_live, weeks_all], bins=30, density=True, edgecolor='black', alpha=0.7, histtype='barstacked')

结果如下，上图参数值为 bar，数据左右并列；下图参数值为 barstack，数据上下重叠。

第一胎的宝宝经常晚于预产期出生吗？

这是书中刚开头便抛出的统计学问题，在有了统计数据后，便可以对该假设做进一步验证了。作者在本章中只是对结论作出了直观说明，并没有给出统计学证明（查询目录后发现作者在第九章中证明了），这里我将尝试使用统计学方法对该问题进行假设检验。步骤如下：
（1）首先分别观测头胎和非头胎母亲的怀孕周数数据
分别绘制直方图

live = df[df['outcome']==1]
firsts = live.prglngth[live['birthord']==1].dropna() # 头胎数据
others = live.prglngth[live['birthord']!=1].dropna() # 非头胎数据
hist = plt.hist([firsts, others], bins=30, density=True, edgecolor='black', alpha=0.7)

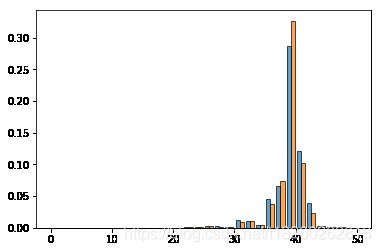
基本认为数据满足正态分布，且样本数量足够大，故可选用z检验方法。
（2）进行z检验
首先确定原假设和备择假设
$H_0$：$W_{fir}\le W_{oth}$ ；$H_1$： $W_{fir}>W_{oth}$
并设定显著性水平为 $\alpha =0.05$
接下来就可以进行z检验了

fir_avg, oth_avg = firsts.mean(), others.mean() # 均值
fir_var, oth_var = firsts.var(), others.var() # 方差
# 进行z检验
pooled_var = fir_var / len(firsts) + oth_var / len(others)
diff = (fir_avg - oth_avg) / pooled_var ** 0.5

得到$z=1.377$，小于临界值$u_{1-\alpha }=1.645$，故接受原假设$H_0$，认为：头胎产妇平均怀孕周数不大于非头胎产妇平均怀孕周数。