第十一章 散列表

11.1 直接寻址表

11.1-1 假设一动态集合S用一个长度为m的直接寻址表T来表示。请给出一个查找S中最大元素的过程。你所给的过程在最坏情况下的运行时间是多少？
Θ（1）

11.1-2 位向量是一个仅包含0和1的数组。长度为m的位向量所占空间要比包含m个指针的数组少得多。请说明如何用一个为向量来表示一个包含不同元素（无卫星数据）的动态集合。字典操作的运行时间应为O（1）。

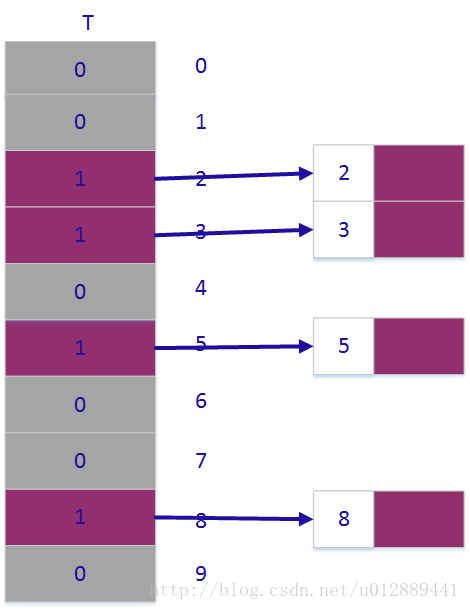
如图所示，寻址表T中，1表示有元素，0表示没有元素，然后分别在各自的存储区中存储卫星数据。

11.1-3 试说明如何实现一个直接寻址表，表中各元素的关键字不必都不相同，且各元素可以有卫星数据。所有三种字典操作（INSERT、DELETE和SEARCH）的运行时间应为O（1）。（不要忘记DELETE要处理的是被删除对象的指针变量，而不是关键字。）

可以在T表中直接存取对象，也可以像上题中通过指针的方式寻找。

11.2 散列表

11.2-1假设用一个散列函数h将n个不同的关键字散列到一个长度为m的数组T中。假设采用的是简单均匀散列，那么期望的冲突数是多少？更准确地，集合{k,l}：k≠l，且h（k）=h（l）基的期望值是多少？

E[Y]=E[∑k≠lXkl]=∑k≠lE[Xkl]=n(n−1)2∗1m=n(n−1)2m

11.2-2 对于一个用链接法解决冲突的散列表，说明将关键字5，28，19，15，20，33，12，17，10插入到该表中的过程。设该表中有9个槽位，并设其散列函数为h(k)=k mod 9。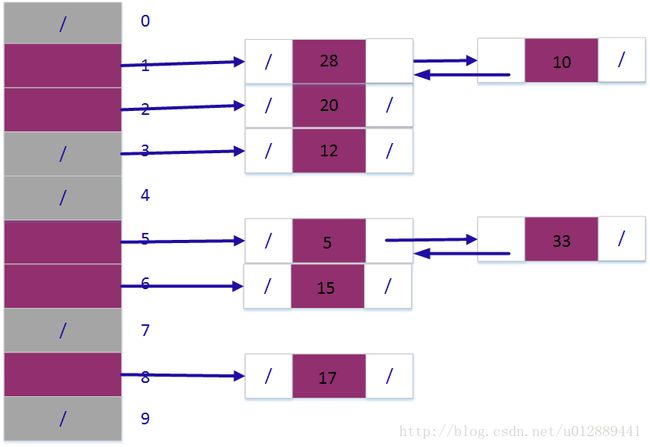

11-2.3 Marley 教授做了这样一个假设，即如果将链模式改动一下，使得每个链表都能保持已排好序的顺序，散列的性能就可以有较大的提高。Marley教授的改动对成功查找、不成功查找、插入和删除操作的运行时间有何影响？
减少不成功查找的时间，只要找到比操作数大的键值就可以不继续向下查找。
对于成功查找和删除操作，时间可能大也可能小，因为元素查找到的随机性。
对于插入操作，有原来的头插法，变成找到位置再插入，增加运行时间。

11-2.4 说明在散列表内部，如何通过将所有未占用的槽位链接成一个空闲链表，来分配和释放元素所占的存储空间。假定一个槽位可以存储一个标志、一个元素加上一个或两个指针。所有的字典和空闲链表操作均应具有O（1）的期望运行时间。该空闲链表需要的是双向链表吗？或者是不是单链表就足够了呢？

以下答案来源于英文答案

The flag in each slot will indicate whether the slot is free.(每个槽位的标志位将指明这个槽位是否为空)。
*A free slot is in the free list, a doubly linked list of all free slots in the table.The slot thus contains two pointers.(每个空槽包含两个指针，位于一个将所有空槽位双向链接的链表中)。
* A used slot contains an element and a pointer(possibly NIL) to the next element that hashes to this slot.(Of course , that pointer points to another slot in the table.)(一个占用的槽位包含了一个元素和指向下一个元素的指针，下一个元素可以为空。（当然，这个指针指向的元素也在表格中。）)
操作
*Insertion：
*If the element hashes to a free slot, just remove the slot from the free list and store the element there(with a NIL pointer). The free list must be doubly linked in order for this deletion to run in O(1) time.(如果这个元素哈希映射到一个空槽位，只需要从空槽位链表移除这个节点并且存储这个元素（指向下一个元素的指针为空）。存储空槽位的链表必须是双向链接的为了保证删除操作的运行时间为O（1）。)
* If the element hashes to a used slot j,check whether the element x already there “belongs” there (its key also hashes to slot j).(如果这个元素映射到占用着的槽点j，检查是否x元素已经属于这个槽点j了。)
*If so,add the new element to the chain of elements in this slot. To do so,allocate a free slot(e.g.,take the head of the free list ) for the new element and put this new slot at the head of the list pointed to by the hashed-to slot(j).(如果是，将这个元素增加到槽位的链中，为这个新元素分配一个槽位的空间然后将这个新槽点以头插法的方式插入到槽位对应的链中。)
* If not ,E is part of another slot’s chain. Move it to a new slot by allocating one from the free list ,copying the old slot’s(j’s) contents(element x and pointer ) to the new slot , and updating the pointer in the slot that pointed to j to point to the new slot. Then insert the new element in the now-empty slot as usual.(如果不是，E是这个槽位链的一部分。将它移动到一个新槽位：从空链表分配空间，复制这个元素内容到新的槽位，然后更新的这个槽位的指针，把指向j的指针指向这个新槽位。然后插入这个新元素到这个空槽位中)To update the pointer to j,it is necessary to find it by searching the chain of elements starting in the slot x hashes to .(为了更新指向j的指针，从槽位x哈希映射的位置开始查找指向元素的链是非常重要的。)
*Deletion：Let j be the slot the element x to be delete hashes to.(删除：让j槽位上的x元素从哈希表中移除)
*If x is the only element in j(j doesn’t point to any other entries), just free the slot ,returning it to the head of the free list.(如果x是j上的唯一一个元素 ，只需要释放这个节点，返回它到这个空链表中）。
* If x is in j but there’s pointer to a chain of other elements, move the first pointed-to entry to slot j and free the slot it was in.(如果x指向j但是它的指针指向链中的其他元素，移除第一个指向j的元素并释放它)
* If x is found by following a pointer from j, just free x’s slot and splice it out of the chain(如果 x在j之后的链中，将x从链中移除并释放x槽位)
*Searching: Check the slot the key hashes to , and if that is not the desired element, follow the chain of pointers from the slot. (搜索：检查这个关键字映射的槽位，同时如果它不是你要的元素，查找指针指向的下一个节点。)
All the operations take expected O(1)times for the same reason they to with the version in the book:The expected time to search the chains is O(1+α) regardless of where the chains are stored ,and the fact that all the elements are stored in the table means that α<=1.If the free list were singly linked , then operations that involved removing an arbitrary slot from the free list would not run in O(1) time.（所有的操作都期望用O(1)的运行时间，就像他们在书中提到的：查询链的期望时间是O(1+α)）,无论链表是怎样存储的，如果所有元素都存储在表中，那么α≤1。如果空链表是单链，这些包括从空链表移除随机槽位的运行时间不会达到O（1）。）

11.2-5 假设将一个具有n个关键字的集合存储到一个大小为m的散列表中。试说明如果这些关键字均源于全域U，且|U|＞nm,则U中还有一个大小为n的子集，其由散列到同一槽位中的所有关键字构成，使得链接法散列的查找时间最坏情况下为Θ（n）。
n个关键字可能存储在m的任何一个位置，m的任意一个槽位可能存储全部的n。故全域|U|>mn。那么U中包含了所有可能节点的集合。也就包含了映射到同一槽位的关键字集合。这时链表散列查找要从头查到尾，故最坏查找时间为Θ（n）。
α = n / m，L为最长链长度，即L ≥ α。所以L(1+ 1/α) ≥ 1 + α。又成功查找期望时间为O(1 + α)，即 O( L(1 + 1 / α) )。

11.3 散列函数

11.3-1 假设我们希望查找一个长度为n的链表，其中每一个元素都包含一个关键字k并具有散列值h（k）。每一个关键字都是长字符串。那么在表中查找具有给定关键字的元素时，如何利用各元素的散列值呢？
将k的值代入h的元素中，通过h（k）去查找元素。

11.3-2 假设将一个长度为r的字符串散列到m个槽中，并将其视为一个以128为基数的数，要求应用除法散列法。我们可以很容易地把数m表示为一个32位的机器字，但对长度为r的字符串，由于它被当做以128为基数的数来处理，就要占用若干个机器字。假设应用除法散列法来计算一个字符串的散列值，那么如何才能在除了该串本身占用的空间外，只利用常数个机器字？

k=∑i=0ns[i]∗128ih(k)=∑i=0n((s[i]  mod  m)∗(128i  mod  m))mod  m

11.3-3 考虑除法散列法的另一种版本，其中h(k)=k mod m, m=2p−1 ,k为按基数 2p 表示的字符串。试证明：如果串x可由串y通过其自身的字符置换排列导出，则x和y具有相同
的散列值。给出一个应用的例子，其中这一特性在散列函数中是不希望出现的。

k(x)=∑i=0ns[i]∗(2p)tik(y)=∑i=0ns[i]∗(2p)rih(k(x))=k(x) mod m=(∑i=0ns[i]∗(2p mod(2p−1))ti)mod m=(∑i=0ns[i]∗1)mod m=h(k(y))

11.3-4 考虑一个大小为m=1000的散列表和一个对应的散列函数 h（k）=⌊m(kAmod1)⌋ ,其中A= (5√−1)/2 ,试计算关键字61、62、63、64和65被映射到的位置。
散列值分别为：700、318、936、554、172

11.4 开放寻址法

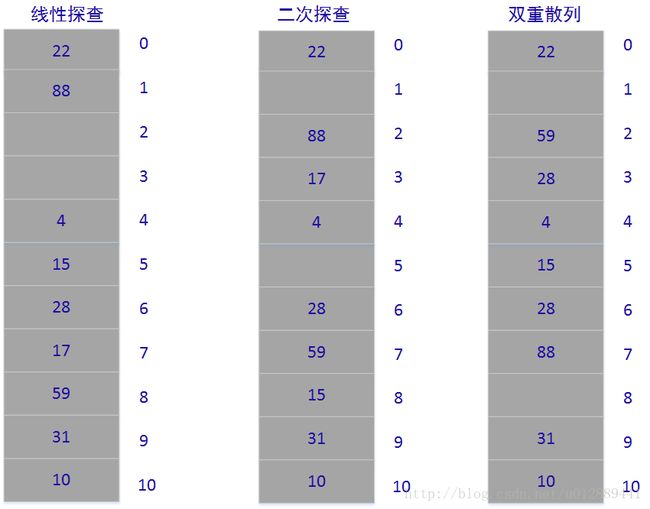
11.4-1 考虑用开放寻址法将关键字10、22、31、4、15、28、17、88、59插入到一长度为m=11的散列表中，辅助散列函数为h’(k)=k。试说明分别用线性探查、二次探查（ c1=1，c2=3 ）和双重散列（ h1(k)=k,h2(k)=1+(kmod(m−1)) )将这些关键字插入散列表的过程。

11.4-2 试写出HASH-DELETE的伪代码；修改HASH-INSERT，使之能处理特殊值DELETED。
HASH-INSERT(T,k)
i=0
repeat
j==h(h,i)
if T[j]==NIL||T[j]==DELETED
T[j]=k
return j
else i=i+1
until i==m
error “hash table overflow”

HASH-INSERT(k)
repeat
j==h(h,i)
if T[j]==k
T[j]=DELETED
return
else i=i+1
until i==m
error “key is not found”

11.4-3 考虑一个采用均匀散列的开放寻址散列表。当装载因子为3/4和7/8时，试分别给出一次不成功查找和一次成功查找的探查期望数上界。

1/(1-3/4)=4次
1/(1-7/8)=8次