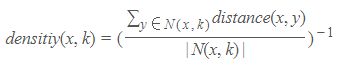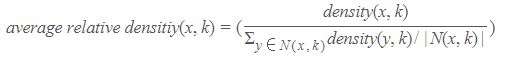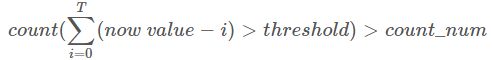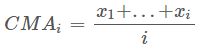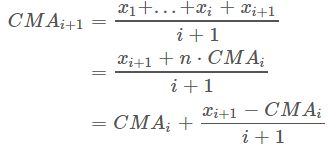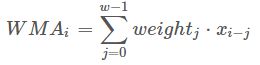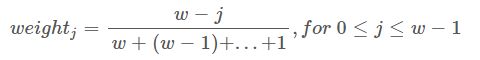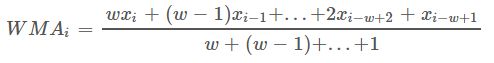基于时间序列的异常检测
目录
1 异常检测
1.1 基于模型的方法
1.2 基于距离的方法/基于邻近度的方法
1.3 基于密度的方法
1.4 基于聚类的方法
1.5 基于划分的方法
1.6 基于线性的方法
1.7 基于非线性的方法
1.8 针对非数值型的方法
1.9 基于深度学习的方法
1.10 总结
2 基于时间序列的异常检测方法
2.1 短期环比(SS)
2.1.1 动态阈值
2.1.2 窗口特征
2.1.3 分类方法
2.2 长期环比(LS)
2.3 同比(chain)
2.4 同比振幅(CA)
2.5 算法组合
2.6 其他方法
2.7 相空间重构
1 异常检测
1.1 基于模型的方法
许多异常检测技术首先建立一个数据模型。异常是那些同模型不能完美拟合的对象。例如,数据分布模型可以通过估计概率分布的参数来创建。如果一个对象不能很好地同该模型拟合,即如果它很可能不服从该分布,则它是一个异常。如果模型是簇的集合,则异常是不显著属于任何簇的对象。在使用回归模型时,异常是相对远离预测值的对象。
由于异常和正常对象可以看作两个不同的类,因此可以使用分类方法来建立这两个类的模型。当然,仅当某些对象存在类标号,使得我们可以构造训练数据集时才可以使用分类方法。此外,异常相对稀少,在选择分类方法和评估度量是需要考虑这一因素。
基于模型的方法又称为统计方法,主要通过拟合单个模型或多个模型来判断该点的概率。
1.1.1 单维情况
-
3σ-法则
(μ−3σ,μ+3σ)区间内的概率为99.74。所以可以认为,当数据分布区间超过这个区间时,即可认为是异常数据。
-
箱型图
IQR是第三四分位数减去第一四分位数,大于Q3+1.5*IQR之外的数和小于Q1-1.5*IQR的值被认为是异常值。
-
Grubbs测试
Grubbs测试是一种从样本中找出outlier的方法,所谓outlier,是指样本中偏离平均值过远的数据,他们有可能是极端情况下的正常数据,也有可能是测量过程中的错误数据。使用Grubbs测试需要总体是正态分布的。
算法流程:
- 样本从小到大排序
- 求样本的mean和std.dev
- 计算min,max(最小值和最大值)与mean的差距,更大的那个为可疑值
- 求可疑值的z-score (standard score),如果大于Grubbs临界值,那么就是outlier;
Grubbs临界值可以查表得到,它由两个值决定:检出水平α(越严格越小),样本数量n。排除outlier,对剩余序列循环做 1-4 步骤。由于这里需要的是异常判定,只需要判断tail_avg是否outlier即可。
https://blog.csdn.net/sunshihua12829/article/details/49047087
1.1.2 高维情况
- Mahalanobis距离
- X2统计
- 单个/混合高斯分布
在某些情况下,很难建立模型,例如,因为数据的统计分布未知或没有训练数据可用。在这些情况下,可以使用如下所述的不需要模型的技术。
1.2 基于距离的方法/基于邻近度的方法
通常可以在对象之间定义邻近性度量,并且许多异常检测方法都基于邻近度。异常对象是那些远离大部分其他对象的对象。这一领域的许多方法都基于距离,称作基于距离的离群点检测方法。当数据能够以二维或三维散布图显示时,通过寻找与大部分其他点分离的点,可以从视觉上检测出基于距离的离群点。
但是该方法计算复杂度过高,且分布不均匀的点,容易出错。
1.2.1 基于角度的离群点检测
角度越小,说明距离越远。
1.2.2 k-最近邻
到k-最近邻的距离。评分为数据对象与最近的k个点的距离之和。很明显,与k个最近点的距离之和越小,异常分越低;与k个最近点的距离之和越大,异常分越大。设定一个距离的阈值,异常分高于这个阈值,对应的数据对象就是异常点。
1.2.3 Local Outlier Factor(LOF)
LOF得分为数据对象的k个最近邻的平均局部密度与数据对象本身的局部密度之比。
1.2.4 Connectivity Outlier Factor(COF)
如果点 p 的平均连接距离大于它的 k最近邻的平均连接距离,则点 p是异常点。COF将异常值识别为其邻域比其近邻的邻域更稀疏的点。
1.2.5 stochastic outlier selection algorithm(无监督)
基于方差,近邻点越多,方差越小;近邻点越大,方差越大。
1.3 基于密度的方法
对象的密度估计可以相对直接地计算,特别是当对象之间存在邻近性度量时,低密度区域中的对象相对远离近邻,可能被看作异常。一种更复杂的方法考虑到数据集可能有不同密度区域这一事实,仅当一个点的局部密度显著地低于它的大部分近邻时才将其分类为离群点。
1.3.1 定义1:基于密度的异常
异常就是那些在低密度区域的数据对象,一个数据对象的异常分就是该对象所在区域的密度的倒数,下面是基于密度的异常分的计算公式:
其中N(x,k)指的是x的k个最近的邻居的集合,|N(x,k)|表示该集合的大小,y是x最近的邻居。
1.3.2 定义2:给定半径的邻域内的数据对象数
一个数据对象的密度等于半径为d的邻域内的数据对象数。
d 的选择很重要,若 d 太小,则会有很多正常的数据对象被认为是异常点;若d太大,则很多异常数据对象会被误判为正常点。事实上,当密度分布不均匀的时候,上述方法得到的异常点会不正确。为了克服密度不均匀的情况,我们使用下面的平均相对密度来作为异常分。
1.3.3 定义3:平均相对密度
1.3.4 基于相对密度的异常检测算法
- {k是最近邻的个数}(类似KNN中的k)
- for 所有的数据对象x do
- 计算N(x,k)
- 计算density(x,k)
- end for
- for 所有的数据对象x do
- outlier score(x)=average relative density(x,k)
- end for
- 取outlier score最大的N个数据对象作为异常
1.4 基于聚类的方法
一种利用聚类检测离群点的方法是丢弃远离其他簇的小簇。这种方法可以与任何聚类方法一起使用,但是需要最小簇大小和小簇与其他簇之间距离的國值。通常,该过程可以简化为丢弃小于某个最小尺寸的所有簇。这种方案对簇个数的选择高度敏感。此外,使用这一方案,很难将离群点得分附加在对象上。注意,把一组对像看作离群点,将离群点的概念从个体对象扩展到对象组,但是本质上没有任何改变。
一种更系统的方法是,首先聚类所有对象,然后评估对象属于簇的程度。对于基于原型的聚类,可以用对象到它的簇中心的距离来度量对象属于簇的程度。更一般地,对于基于目标函数的聚类方法,可以使用该目标函数来评估对象属于任意簇的程度。特殊情况下,如果删除一个对象导致该目标的显著改进,则我们可以将对象分类为离群点。如,对于K均值,删除远离其相关簇中心的对象能够显著地改进簇的误差的平方和(SSE)。总而言之,聚类创建数据的模型,而异常扭曲模型。
1.5 基于划分的方法
- 孤立森林
基于划分的思想,划分成树,深度越低,说明越容易被划分,即为离群点。
https://blog.csdn.net/weixin_39910711/article/details/106535320
- https://www.jianshu.com/p/4d817084a69a
- https://www.jianshu.com/p/5af3c66e0410
- http://www.cnblogs.com/fengfenggirl/p/iForest.html
1.6 基于线性的方法
- Principal Component Analysis(PCA)
- 机器学习算法(五):主成分分析PCA:https://blog.csdn.net/weixin_39910711/article/details/82314632
PCA在做特征值分解之后得到的特征向量反应了原始数据方差变化程度的不同方向,特征值为数据在对应方向上的方差大小。所以,最大特征值对应的特征向量为数据方差最大的方向,最小特征值对应的特征向量为数据方差最小的方向。原始数据在不同方向上的方差变化反应了其内在特点。如果单个数据样本跟整体数据样本表现出的特点不太一致,比如在某些方向上跟其它数据样本偏离较大,可能就表示该数据样本是一个异常点。
1.7 基于非线性的方法
- Replicator Neural Networks(RNNs)
- AutoEncoder(AE):Anomaly Detection异常检测的几种方法
- Variational AutoEncoder(VAE):AIOps探索:基于VAE模型的周期性KPI异常检测方法
1.8 针对非数值型的方法
- Attribute Value Frequency
针对非数值型的数据,即类别离散数据的方法。
1.9 基于深度学习的方法
- Deep Learning for Anomaly Detection: A Survey
相关综述可以阅读上面的文献。另外,随着贝叶斯与深度网络的结合,能够衡量模型的不确定性的贝叶斯深度网络在各个领域中应用广泛,也诞生了很多专门针对于神经网络计算不确定性的方法,具体文献可以参考Uncertainty in Deep Learning。另外一篇博客介绍的Uber用于预测和检测的一个框架,就是基于不确定性的思路做的。
1.10 总结
可以看到,以上方法的分类之间也是相近的,说到底,概率、密度和聚类也是由空间中的数据点之间的距离所决定的。而本文主要是想记录基于时间序列的异常检测方法,当然,以上的方法,在时间序列抽取后的特征空间中也能够使用。
2 基于时间序列的异常检测方法
- 同比,是指在相邻时段中的某一相同时间点进行比较。
- 环比,是指在同一时段中的相邻时间点进行比较。
2.1 短期环比(SS)
对于时间序列(是指将同一统计指标的数值按其发生的时间先后顺序排列而成的数列)来说,T 时刻的数值对于 T−1 时刻有很强的依赖性。比如流量在8:00很多,在8:01时刻的概率是很大的,但是如果07:01时刻对于8:01时刻影响不是很大。
首先,我们可以使用最近时间窗口(T)内的数据遵循某种趋势的现象来做文章。比如我们将 T 设置为7,则我们取检测值(now value)和过去7个(记为i)点进行比较,如果大于阈值我们将 count 加1,如果 count 超过我们设置的count num,则认为该点是异常点。
上面的公式涉及到 threshold 和count num两个参数,threshold 如何获取我们将在下节进行介绍,而count num可以根据的需求进行设置,比如对异常敏感,可以设置count num小一些,而如果对异常不敏感,可以将count num设置的大一些。
2.1.1 动态阈值
业界关于动态阈值设置的方法有很多,这里介绍一种针对360的lvs流量异常检测的阈值设置方法。通常阈值设置方法会参考过去一段时间内的均值、最大值以及最小值,我们也同样应用此方法。取过去一段时间(比如TT窗口)的平均值、最大值以及最小值,然后取 max−avg 和 avg−min 的最小值。之所以取最小值的原因是让筛选条件设置的宽松一些,让更多的值通过此条件,减少一些漏报的事件。
![]()
2.1.2 窗口特征
一、统计特征
(1)3-sigma
(2)z score
(3)Grubbs格拉斯测试
(4)moving average(移动平均)
(5)cumulative moving average(累加移动平均)
(6)weighted moving average(加权移动平均)
(7)exponential weighted moving average(指数加权移动平均)
(8)double exponential smoothing(双指数平滑)
(9)triple exponential smoothing(三指数平滑)(Holt-Winters)
(10)stddev from average(平均值-标准差)
(11)stddev from moving average(移动平均-标准差)
(12)stddev from ewma(指数加权移动平均-标准差)
(13)histogram bins
(14)median absolute deviation(中位数绝对偏差)
(15)median of deviation(MAD)
(16)mean subtraction cumulation(平均值减法累积?)
(17)first hour average(前若干-平均值)
二、熵特征
(1)Binned Entropy
(2)Approximate Entropy
(3)Sample Entropy
三、分段特征
(1)分段聚合逼近(Piecewise Aggregate Approximation)—- 类似 Riemann 积分
(2)符号逼近(Symbolic Approximation)—- 类似 Riemann 积分
四、总特征
一、统计特征
(1)3-sigma
一个很直接的异常判定思路是,拿最新3个datapoint的平均值(tail_avg方法)和整个序列比较,看是否偏离总体平均水平太多。怎样算“太多”呢,因为standard deviation表示集合中元素到mean的平均偏移距离,因此最简单就是和它进行比较。在normal distribution(正态分布)中,99.73%的数据都在偏离mean 3个σ (standard deviation 标准差) 的范围内。如果某些datapoint 到 mean 的距离超过这个范围,则认为是异常的。
(2)z score
标准分,一个个体到集合mean的偏离,以标准差为单位,表达个体距mean相对“平均偏离水平(std dev表达)”的偏离程度,常用来比对来自不同集合的数据。
在模型中,z_score用来衡量窗口数据中,中间值的偏离程度。
算法流程:
- 排除最后一个值
- 求剩余序列的平均值
- 全序列减去上面这个平均值
- 求剩余序列的标准差
- ( 中间三个数的平均值-全序列均值)/ 全序列标准差
(3)Grubbs格拉斯测试
Grubbs测试是一种从样本中找出outlier的方法,所谓outlier,是指样本中偏离平均值过远的数据,他们有可能是极端情况下的正常数据,也有可能是测量过程中的错误数据。使用Grubbs测试需要总体是正态分布的。
算法流程:
- 样本从小到大排序
- 求样本的mean和std.dev
- 计算min/max与mean的差距,更大的那个为可疑值
- 求可疑值的z-score (standard score),如果大于Grubbs临界值,那么就是outlier;
Grubbs临界值可以查表得到,它由两个值决定:检出水平α(越严格越小),样本数量n。排除outlier,对剩余序列循环做 1-4 步骤。由于这里需要的是异常判定,只需要判断tail_avg是否outlier即可。
(4)moving average(移动平均)
给定一个时间序列和窗口长度N,moving average等于当前data point之前N个点(包括当前点)的平均值。不停地移动这个窗口,就得到移动平均曲线。
移动平均法不考虑较远期的数据。
(5)cumulative moving average(累加移动平均)
设 {xi:i≥1} 是观察到的数据序列。 累积移动平均线是所有数据的未加权平均值。 如果若干天的值是 x1,…,xi,那么
当有新的值 xi+1,那么累积移动平均为
(6)weighted moving average(加权移动平均)
加权移动平均值是先前w个数据的加权平均值。 假设![]() ,其中
,其中![]() ,则加权移动平均值为,
,则加权移动平均值为,
一般,
所以,
在加权移动平均法中不考虑较远期的数据,并给予近期资料更大的权重。
(7)exponential weighted moving average(指数加权移动平均 EWMA)
https://www.cnblogs.com/jiangxinyang/p/9705198.html
指数移动与移动平均有些不同:
- 并没有时间窗口,用的是从时间序列第一个data point到当前data point之间的所有点。
- 每个data point 的权重不同,离当前时间点越近的点的权重越大,历史时间点的权重随着离当前时间点的距离呈指数衰减,从当前data point往前的data point,权重依次为
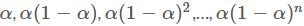 。
。
该算法可以检测一个异常较短时间后发生另外一个异常的情况,异常持续一段时间后可能被判定为正常。
(8)double exponential smoothing(双指数平滑)
https://wiki.mbalib.com/wiki/%E6%8C%87%E6%95%B0%E5%B9%B3%E6%BB%91%E6%B3%95
http://vlambda.com/wz_wFFN2DvEJb.html
https://blog.csdn.net/anshuai_aw1/article/details/82499095
https://baijiahao.baidu.com/s?id=1674531308711991130&wfr=spider&for=pc
预测算法——指数平滑法:https://blog.csdn.net/nieson2012/article/details/51980943
2.1.3 分类方法
2.2 长期环比(LS)
2.3 同比(chain)
2.4 同比振幅(CA)
2.5 算法组合
2.6 其他方法
2.7 相空间重构
http://blog.rexking6.top/2018/11/05/%E5%9F%BA%E4%BA%8E%E6%97%B6%E9%97%B4%E5%BA%8F%E5%88%97%E7%9A%84%E5%BC%82%E5%B8%B8%E6%A3%80%E6%B5%8B/