平衡二叉树的C语言实现
平衡二叉树的结构
//平衡二叉树相对于二叉排序树的数据结构增加了平衡因子和父亲节点
typedef struct T{
int data;//节点数据
int bal;//平衡因子
struct T *lchild,*rchild,*parent;//左孩子、右孩子、父亲节点
}*BiTree,LNode;平衡二叉树的旋转操作
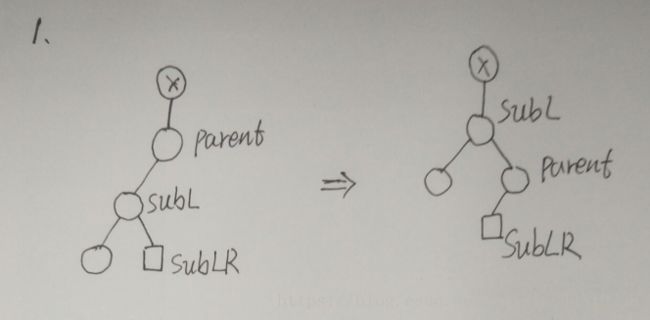
当某一节点的平衡因子的绝对值大于一时,则不满足平衡二叉树的定义,需要将其进行旋转操作,使其保持平衡。设不平衡点为parent,parent的父亲节点为x,parent的左孩子为SubL,右孩子为SubR,SubL的右孩子为SubLR,SubR的左海子为SunRL,旋转操作共有四种(对parent进行旋转操作):
- 左单旋转:SubLR成为parent的左孩子,parent成为SubL的左孩子,SubL成为x的左孩子或右孩子;
- 右单旋转:SubRL成为parent的右孩子,parent成为SubR的左孩子,SubR成为x的左孩子或右孩子
- 右左双旋转:对SubL进行一次右单旋转,再对parent进行左单旋转
- 左右双旋转:对SubR进行一次左单旋转,再对parent进行右单旋转
具体旋转变化入下图所示:
- 右单旋转的代码实现
//传参 parent 是最小不平衡子树的根节点 T是整棵树的根节点指针
//传参类型为指针的地址
void RotateRight(BiTree *parent,BiTree *T){
LNode *x=(*parent)->parent;//记录父亲节点
LNode *SubL=(*parent)->lchild;//记录根节点的左孩子
LNode *SubLR=SubL->rchild;//根节点左孩子的右孩子
//parent的左孩子为SubLR
(*parent)->lchild=SubLR;
if(SubLR){
SubLR->parent=(*parent);
}
//SubL的右孩子为parent
SubL->rchild=(*parent);
(*parent)->parent=SubL;
/*--更新x的孩子节点--*/
//若x不存在,则说明parent即是根节点
if(!x){
(*T)=SubL;
SubL->parent=NULL;
}
//存在则判断parent是x的左孩子还是右孩子,SubL替换
else{
if(x->lchild==(*parent)){
x->lchild=SubL;
}
else{
x->rchild=SubL;
}
SubL->parent=x;
}
}- 左单旋转的代码实现
void RotateLeft(BiTree *parent,BiTree *T){
LNode *x=(*parent)->parent;
LNode *SubR=(*parent)->rchild;
LNode *SubRL=SubR->lchild;
//parent的右孩子为SubRL
(*parent)->rchild=SubRL;
if(SubRL){
SubRL->parent=(*parent);
}
//SubR的左孩子为parent
SubR->lchild=(*parent);
(*parent)->parent=SubR;
//x的孩子为SubR
if(!x){
(*T)=SubR;
SubR->parent=NULL;
}
else{
if(x->lchild==(*parent)){
x->lchild=SubR;
}
else{
x->rchild=SubR;
}
SubR->parent=x;
}
}- 左右双旋转变化
void RotateLR(BiTree *parent,BiTree *T){
//先对SubL进行左转变化、再对parent进行右转变化
RotateLeft(&((*parent)->lchild),T);
RotateRight(parent,T);
}- 右左双旋转变化
void RotateRL(BiTree *parent,BiTree *T){
RotateRight(&((*parent)->rchild),T);
RotateLeft(parent,T);
}注:因为左单旋转和右单旋转是对称的,所以可加入参数dir=0 or 1 进行判断,使左单旋转和右单旋转可通过一个函数实现,具体参考王晓东的数据结构。
求平衡因子(注:等于右子树的高度减左子树的高度,在之后对操作的判断中是关键因素)
/*--------------------求平衡因子----------------*/
//计算树的高度 这里使用递归求树的高度
int Height(BiTree T){
int n,m;
if(T==NULL){
return 0;
}
n=Height(T->rchild);
m=Height(T->lchild);
if(m>n){
return m+1;
}
else{
return n+1;
}
}
/*
该节点的平衡因子等于右子树的高度减左子树的高度
递归求解
*/
void Calbalance(BiTree T){
if(T==NULL){
return ;
}
T->bal=Height(T->rchild)-Height(T->lchild);//此处是右树高度减左树高度,在重新平衡的判定中起到作用
//printf("%d %d\n",T->data,T->bal);
Calbalance(T->rchild);
Calbalance(T->lchild);
}插入操作
平衡二叉树的插入操作和二叉树的插入操作类型,只是在插入操作结束之后,有可能会引起失衡,此时需要进行旋转操作使平衡二叉树继续保持平衡。
- 失衡分析
设插入节点为p,插入节点的父亲节点为x,现考察x节点的父亲节点parent。有三种情形:
- 当 abs(parent->bal) = 1 ,树保持平衡,但以parent为根节点的子树的高度增加1,即需向上回溯检查parent的父节点。
- 当abs(parent->bal) = 0, 树保持平衡,且以parent为根节点的子树高度不变,即结束运算
- 当abs(parent->bal) > 1, 树失去平衡,此时考察节点x判读破坏平衡的节点发生在哪里,此时有四种情况
parent->bal = -2 && parent->lchild->bal = 1 此时的操作是左右双旋转
parent->bal = -2 && parent->lchild->bal = -1 此时的操作是左单旋转
parent->bal = 2 && parent->rchild->bal = 1 此时的操作是左单旋转
parent->bal = 2 && parent->rchild->bal = -1 此时的操作是右左单旋转
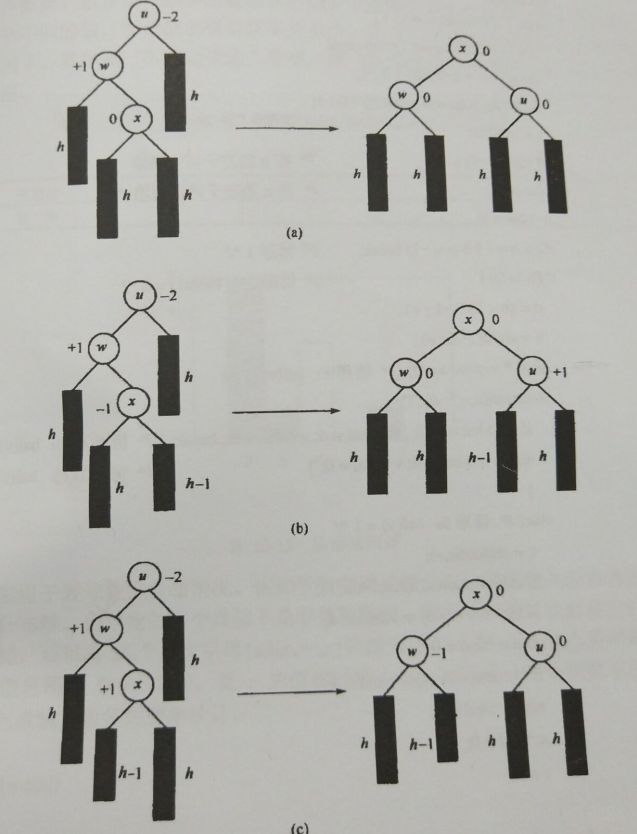
- 情形3中四种情况的图示
- 情形1:节点加一,使树的根节点平衡因子变为一,说明新增的节点使左子树或者右子树的高度超过原来的高度,即整棵子树的高度增一,此时需向上继续考察。
- 情形2:节点加一,使树的根节点的平衡因子变为0,说明新增的节点并没有改变原来子树的高度,故结束运算。
- 插入运算维护平衡的代码实现
void InsertBalance(BiTree *x,BiTree *T){
LNode *parent=NULL;
//x节点是插入节点的父亲节点
//若插入节点不是树根结点
if(*x){
parent=(*x)->parent;//考察其父亲节点
while(parent){
//情形3
if(parent->bal<-1){
if(parent->lchild->bal==-1){
RotateRight(&parent,T);
}
else{
RotateLR(&parent,T);
}
break;
}
if(parent->bal>1){
if(parent->rchild->bal==1){
RotateLeft(&parent,T);
}
else{
RotateRL(&parent,T);
}
break;
}
//情形2
else if(parent->bal==0){
break;
}
//情形1
parent=parent->parent;
}
}
}- 插入运算的实现
//创建新节点
LNode* NewNode(int data){
LNode *p=(LNode *)malloc(sizeof(LNode));
p->bal=0;
p->data=data;
p->lchild=NULL;
p->parent=NULL;
p->rchild=NULL;
return p;
}
//平衡二叉树的插入运算
void Insert(BiTree *T,int data){
LNode *parent=NULL;//记录插入节点的父亲节点
LNode *p=(*T);
if((*T)==NULL){
(*T)=NewNode(data);
}
else{
//找到插入位置
while(p){
parent=p;//记录父亲节点
if(p->data==data){
printf("fault :%d\n",p->data);
return;
}
else if(p->data>data){
p=p->lchild;
}
else{
p=p->rchild;
}
}
//创新节点并插入
p=NewNode(data);
if(parent->data>data){
parent->lchild=p;
}
else{
parent->rchild=p;
}
p->parent=parent;
}
//更新平衡因子并维护平衡
Calbalance((*T));
InsertBalance(&parent,T);
Calbalance((*T));
}删除操作
- 失衡分析
平衡二叉树的删除操作和二叉排序树是一致的,但在删除操作后需要对树进行维护,使其仍然保持平衡二叉树的性质。
需要注意的是对于平衡二叉树的删除操作,我所进行的步骤是找到删除节点和替换节点,后用替换节点代替删除节点,并将删除节点删去,而不是调换其数值后删除替换节点。
在此操作中,我们考察替换节点在被替换之前的父节点parent。
- 若parent->bal = 0;说明,这颗树的高度减一,若parent是父亲节点的左孩子,则父亲节点的平衡因子减1,否则加1.并向上回溯,考察其父亲节点。
- 若abs(parent->bal) = 1,则说明这颗子树的高度没有变化,结束运算。
- 当 paretn->bal < -1 则需要旋转变化。且左子树的高度多一,考查其做孩子 Pchild,此时有三种情况:
Pchild->bal = 0时,进行右单旋转,旋转后节点Pchild的平衡因子为1,即可结束运算
Pchild->bal = -1时,进行右单旋转,记Review为Pchild,Review->bal = 0 需要向上进行回溯
Pchild->bal = 1时,设Pchild的右孩子节点为Review,进行左右双旋转,旋转后Review->bal = 0,需要向上进行回溯
(注:平衡因子大于1的情况和小于-1的情况对称,不多加赘述了)
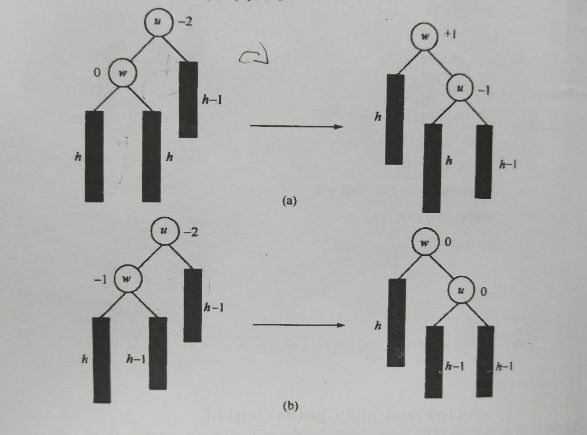
- 图解说明
(parent 即是u,w即是Pchild,x即是Pchild的右孩子,注:Review记录的节点为旋转结束后的根节点,根据其图解分析,根结点平衡因子为0时需要向上继续考察)
- 删除操作维护平衡因子的代码实现
/*传入参数p 是替换节点的父亲节点的地址,T是树的根节点的地址*/
void DeleteBalance(BiTree *T,BiTree *p){
//printf("p: %d %d\n",(*p)->data,(*p)->bal);
LNode *Review=NULL;//记录需要回溯的节点
LNode *Pchild=NULL;//记录p节点的儿子节点
LNode* parent=(*p);//p节点
/*若到根节点则停止或平衡因子绝对值为1*/
if(!parent||abs(parent->bal)==1){
return ;
}
//情形1
else if(parent->bal==0){
//更新节点p的父节点的平衡因子并考察
parent=(*p)->parent;
//若p是右子树则平衡因子减一否则加一
if(parent){
if(parent->rchild==(*p)){
parent->bal--;
}
else{
parent->bal++;
}
DeleteBalance(T,&parent);//回溯
}
//回溯
}
//当平衡因子绝对值等于2的时候
else{
/*
由于运算过程,在回溯时只更新Review节点的平衡因子
并根据其位置将parent节点的平衡因子进行加一或减一
会导致parent->bal的值超过-2或2
所以这里是小于等于
*/
if(parent->bal<=-2){
Pchild=parent->lchild;
if(Pchild->bal==0){
RotateRight(&parent,T);
}
else if(Pchild->bal==-1){
//记录旋转后的根节点
Review=Pchild;
RotateRight(&parent,T);
//更新他的平衡因子为0
Review->bal=0;
DeleteBalance(T,&Review);//回溯
}
else{
//记录旋转后的更节点
Review=Pchild->rchild;
RotateLR(&parent,T);
Review->bal=0;
DeleteBalance(T,&Review);//回溯
}
}
//和上面的情形是对称的
else{
Pchild=parent->rchild;
if(Pchild->bal==0){
RotateLeft(&parent,T);
}
else if(Pchild->bal==1){
Review=Pchild;
RotateLeft(&parent,T);
Review->bal=0;
parent=Review->parent;
DeleteBalance(T,&Review);//回溯
}
else{
Review=Pchild->lchild;
RotateRL(&parent,T);
Review->bal=0;
DeleteBalance(T,&Review);//回溯
}
}
}
}- 删除操作的代码实现
//查找函数
LNode* FindNode(BiTree T,int data){
LNode *p=T;
if(!p){
return 0;
}
while(p){
if(p->data==data){
break;
}
else if(p->data>data){
p=p->lchild;
}
else{
p=p->rchild;
}
}
return p;
}
/*
思路:
找到删除节点、找出替换节点,用替换节点代替删除节点、删掉删除节点
和王晓东的书上略有不同,王晓东的思路是用替换节点的值代替删除节点,后删除替换节点
*/
void DeleteNode(BiTree *T,int data){
LNode *p=FindNode((*T),data);//被删除节点
LNode *x=NULL;//记录被删除点
LNode *parent=NULL;//指向被删节点的父亲
BiTree flag=NULL;//替换节点的父节点
//若存在
if(p){
x=p;//记录被删节点
//如果两个节点都存在
if(p->lchild&&p->rchild){
//找右子树的最小值
p=p->rchild;
if(!p->lchild){
flag=p;
p->lchild=x->lchild;
x->lchild->parent=p;
}
else{
//找到最左值
while(p->lchild){
p=p->lchild;
}
flag=p->parent;
//最左值的父节点
parent=p->parent;
//接管x的左孩子
p->lchild=x->lchild;
x->lchild->parent=p;
//接管p的右孩子
parent->lchild=p->rchild;
if(p->rchild){
p->rchild->parent=parent;
}
//接管x的右孩子
p->rchild=x->rchild;
x->rchild->parent=p;
}
}
//只右子树存在
else if(!p->lchild&&p->rchild){
p=p->rchild;
flag=p;
}
//只左子树存在
else if(p->lchild&&!p->rchild){
p=p->rchild;
flag=p;
}
else{
//若p是叶子节点则直接置空
flag=p->parent;
p=NULL;
}
/*--接管p--*/
parent=x->parent;
//若被删节点是根节点
if(!parent){
(*T)=p;
p->parent=NULL;
}
else{
if(parent->lchild==x){
parent->lchild=p;
}
else{
parent->rchild=p;
}
//入果p不是叶子节点
if(p){
p->parent=parent;
}
}
free(x);
}
//flag是替换节点的父亲节点
//在王晓东书里就是删除节点的父亲节点
Calbalance((*T));
DeleteBalance(T,&flag);
Calbalance((*T));
}其他的实现代码
/*-------测试使用函数-------*/
//队列
typedef struct Qd{
BiTree p[maxsize];
int rear,font;
}Queue;
//访问节点
void visit(BiTree T){
printf("%d ",T->data);
}
//初始化队列
void InitiaQueue(Queue *Q){
(*Q).rear=(*Q).font=0;
}
//判断队空
bool IsEmpty(Queue *Q){
if((*Q).rear==(*Q).font){
return true;
}
else{
return false;
}
}
//入队
void EnQueue(Queue *Q,BiTree p){
(*Q).p[(*Q).font]=p;
(*Q).font++;
}
//出队
BiTree DeQueue(Queue *Q){
int index = (*Q).rear;
(*Q).rear++;
return (*Q).p[index];
}
//层次遍历
bool LevelOrder(BiTree tree){
BiTree p;
Queue Q;
InitiaQueue(&Q);
if(tree!=NULL){
EnQueue(&Q,tree);
}
while(!IsEmpty(&Q)){
p=DeQueue(&Q);
visit(p);
if(p->lchild!=NULL){
EnQueue(&Q,p->lchild);
}
if(p->rchild!=NULL){
EnQueue(&Q,p->rchild);
}
}
}
//先序遍历
bool preOrder(BiTree tree){
if(tree==NULL){
return false;
}
else{
visit(tree);
preOrder(tree->lchild);
preOrder(tree->rchild);
return true;
}
}
int inOrder(BiTree T){
if(T==NULL){
return 0;
}
InOrder(T->lchild);
visit(T);
InOrder(T->rchild);
}
//中序遍历
int InOrder(BiTree T){
if(T==NULL){
return 0;
}
InOrder(T->lchild);
visit(T);
InOrder(T->rchild);
}
//判定是不是一棵平衡二叉树
int Juidge(BiTree T){
if(T==NULL){
return 1;
}
Juidge(T->lchild);
if(abs(T->bal)>1){
printf("%d FAULT! %d\n",T->data,T->bal);
}
Juidge(T->rchild);
}
#include
#include
#include
#define maxsize 100
/*测试数据*/
/* 50 10 80 5 15 70 90 3 8 16 55 71 89 91 7 9 51 58 72 92 57 59 0 */ 总结:写了三天,代码比较复杂,书里的有优化,以后再看看