【Leetcode】记Single Number 三部曲
今天刷LeetCode每日一题推荐的Single Number1 觉得很有意思就顺便做了相关的2 和 3拓展。刚开始做都是有点懵,但是后来看到题解深受启发,记下以备忘!
这三题跟数字逻辑关系挺大的,最近一直在搞FPGA和数字电路相关的东西,关联性还挺强。
目录
一、Single Number 1
二、Single Number 2
三、Single Number 3
一、Single Number 1
如题:
大致意思是: 给定一个非空整型数组,里面的数都是成双成对的,但是有一个是Single dog,将其揪出。
但是有限制,要求时间复杂度是线性的,空间的话不用额外空间。这样的话哈希表的思路直接舍弃。
分析一下:主要目的就是将两个相同的数消掉。在数字逻辑中,两个相同的数异或是0,而任何数和0异或都是都是其本身,并且异或运算满足交换律结合律。
于是,思路就很清晰了。将整个数字的全部元素都异或,最后的结果就是那个Single number。
![]()
C代码如下:
int singleNumber(int* nums, int numsSize){
int res=0;
for(int i =0 ;i这题能想到异或就很简单,想不到就脑壳疼。 算是一种思路的启发吧。
二、Single Number 2
如题:
大致翻译:从第一题的两个成双成对变为成三成吹(tri),但依然有一个Single one ,找出来。
时间复杂度线性,空间复杂度无额外开销。
按照第一题的思路好像有点行不通, 三个相同的数异或还是它本身,等于没处理。
第一题还给了一种启发,位处理!
假设数组为【0,1,0,1,0,1,3】,转为二进制看看:
经过一番找规律,最后的结果应该是每一位上1的个数模上3,有点像数电的模三计数器。
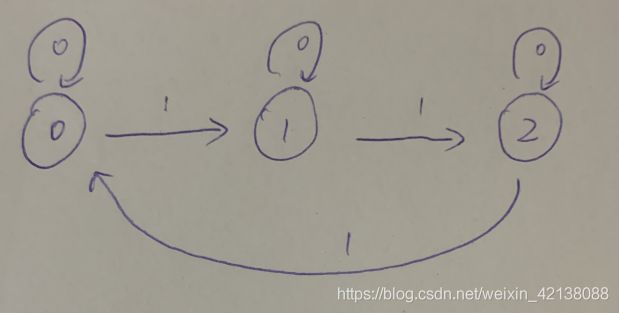
经过题解,看到有用有限状态机的,是一个很好的启发。
三个状态就用两bit来表示 ,分别是00 01 10来表示0,1,2三个状态,用ab来表示,x表示输入,那么状态机的真值表如下所示:
| ab | x | new_ab |
| 00 | 1 | 01 |
| 01 | 1 | 10 |
| 10 | 1 | 00 |
| 00 | 0 | 00 |
| 01 | 0 | 01 |
| 10 | 0 | 10 |
那么,新的状态和上一次的状态就可以用卡诺图化简的方式来获得表达式了:
最后得到的逻辑表达式:
new_a = (x&b)|(~x&a)
new_b = ~a&(x^b)
C代码:
int singleNumber(int* nums, int numsSize){
int a=0,b=0;
int tmp;
int x;
for(int i=0;i
三、Single Number 3
如题:
大致意思是:在一堆成双成对的数组里,现在又两个Single DOG 了 把他们揪出来。要求时间复杂度O(n),空间复杂度O(1)。
这题从Single number 1受启发,可以通过异或将成双成对的消去,但是这次有两个,这样结果就是两个Single Number的异或,如果有办法把这两个不同的Single Number 分离提取出来,那不就成了吗?
问题是如何提取出来呢。。。。。
思路:两个不同的数(分别称他们为x,y吧),则必有一位是不同的,要么是0 要么是1。那么就可以将整个数组分为两派,一派是那个不同位是0的,一派是那个不同位为1的。这样一分家,就拆分成两个Single Number 1 的问题了。
首先 找到必有一位是不同的位。两个不同的数可能有好几位是不同的,选哪个呢,这里选从低到高中的第一个。例如下图中3和5 异或,那么最后的结果是1的那位就是不同的位,我们这里选用第二位来作为将数组分成两类的依据,3的第二位为1的一组和5的第二位为0的一组。为什么这样分,因为有一个操作能直接提取最低的那位1,而保持其他的都为0。这个逻辑就是:a&-a
与自身补码相与就能提取最低的那个1,其余为0.
这样,将这个a&-a和数组中的每一个数按位与,就能筛选出那位是1的一组和那位是0的一组。在那位是1的一组里进行异或就能获取其中一个数x。再通过x和y异或的值 在和x这个值异或就能获取y了,因为![]()
C代码如下:
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* singleNumber(int* nums, int numsSize, int* returnSize){
int *res = (int *)malloc(sizeof(int) * 2);
res[0]=0;
res[1]=0;
int diff=0;
for(int i=0;i