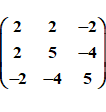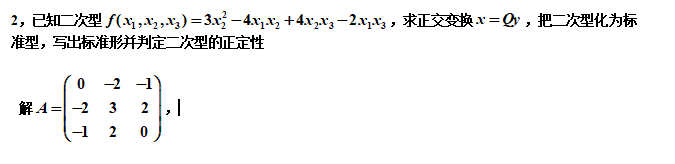含重根的三阶实对称矩阵的快速对角化方法
众所周知,实对称矩阵一定可以相似对角化。而考试中考察的三阶实对称矩阵对角化基本都是三阶的。而且正常情况下特征根一定是整数。因此基于此,有一些特殊的方法可以快速计算三阶实对称矩阵的特征值和特征向量。
一. 猜根法计算特征值
-
特征值之和等于矩阵的对角线元素之和
-
特征值之积等于矩阵的行列式
-
假设矩阵的特征值都是整数
例题1
在假设特征值为整数的情况下,特征值之积为5,特征值之和为3,那么特征值只可能为5,-1 ,-1 因此直接选出答案。
注意:有经验的命题人会把矩阵的行列式的值弄成一个合数。这样就不会一下子被看出来。
二. 秩一矩阵的应用
秩一矩阵是指秩为一的矩阵,由于其特殊性,常常在考试中出现
设A是秩为1的n阶方阵, 则
1. A可表示为αβ^T, 其中α,β为n维列向量
2. A^k = (α^Tβ)^(k-1)A
3. tr(A)=α^Tβ
4. A的特征值为 α^Tβ,0,0,...,0
5. 秩一矩阵一定可以对角化,其中一个特征向量是α
注意:秩一矩阵的直观快速判断法是矩阵为一行都相等或成比例。
定理一:
如果一个矩阵A可以分解为一个秩一矩阵B加上一个常数c乘上单位矩阵,那么这个矩阵A的特征值就是tr(B)+c, c, ..., c。这个矩阵的特征向量和B的特征向量相同。
定理二:
如果一个三阶实对称矩阵具有一个二重特征根,那么一定可以分解为一个秩一矩阵B加上一个常数c乘上单位矩阵
证明: 设这个二重特征根为c,很容易证明R(A-cE) = 1, 令A= A-cE + cE即可。
例题2
求下列矩阵A的特征值和特征向量
A = 2*B - E,其中B为全1矩阵,E为单位矩阵, 显然A的特征值就是5,-1,-1
对于矩阵B来说,很容易看出一个特征向量(1,1,1)^T, 另外两个特征向量分别是(1,-1,0)^T
以及(1,0,-1)^T, 秩一矩阵对应的特征向量是很好求的。如果要求正交矩阵。可以借助向量外积公式来计算。
容易看出,当矩阵能分解为全一矩阵的倍数加上一个常数乘上一个单位阵时,这种情况是最简单。一眼就能看出来怎么分解。
对于一般的例子,很难直接看出怎么分解。解决的办法是先猜/算出特征根,然后再根据算出的二重根分解。
实战演练
很容易计算出来,tr(A)=1, det(A)=-12, 很容易猜出特征根,-3,2,2,计算
A-2E,很容易看出秩一矩阵,证明计算正确。
-3对应的特征向量是(-1,0,2)
2对应的特征向量是(2, 0, 1) 以及(0,1,0) (快速口算)
使用向量外积计算(-1,0, 2) X (0, 1, 0 )
写出正交矩阵
期望这个矩阵出现成比例的情况
所以提出一个E来,矩阵写成 A=B+E,立刻看出矩阵成比例,
期望成比例。