机器学习笔记（三）决策树 - 分类与回归

本文将介绍决策树的实现，以及完成分类与回归任务

一.简介

决策树是一种基于规则的方法，它用一组嵌套的规则进行预测。在树的每个决策节点处，根据判断结果进入一个分支，反复执行这种操作直至达到叶子节点，得到预测结果，这些规则是通过训练得到的，而不是人工制定的。决策树是分段线性函数，具有非线性建模的能力。
                                                                                   ——摘自《机器学习与应用》雷明著

二.决策树-分类

1.分类过程

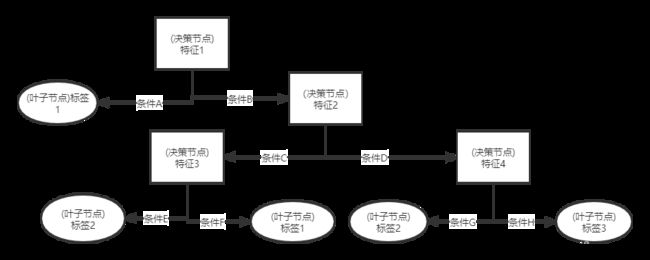
以二叉决策树为例，决策树的决策过程从根节点开始，在每个决策节点处做判断，根据特征向量的某个分量做出判断，将特征向量归为为左子树或右子树，依次进行下去，直至到达叶子节点，叶子节点对应的标签即为分类结果。如下图所示，将一组四维特征向量分为三类的大致过程。

2.训练过程

（1）递归分裂

模型训练的过程就是决策树生长的过程。决策树的建立是一个递归的过程，基本流程为，利用样本集$D$创建根节点，找到一个划分标准，将样本集划分为$D_1$,$D_2$，利用$D_1$,$D_2$分别建立左子节点，右子节点，依次类推，递归地建立整棵树。当不能再分裂时，该节点作为叶子节点，同时确定叶子节点的标签。

（2）最佳分裂及分裂条件

在训练时，我们需要确定一个合适的方法将样本分裂为两部分。
我们的期望是，使分类之后的两部分样本尽可能得“纯”，即同一样本集中的中样本尽可能多得属于同一类。在这里引进信息熵的概念：
$$E(D)=-\sum _i{p}_{i}lo{g}_2{p}_i\text{\hspace{1em}(1)}$$
$p_i=\frac{N_i}{N}$，$N_i$为第$i$类的样本数，$N$为总样本数
$E(D)$越大，说明样本信息量越大，即样本越均匀得分布于不同类，即越不纯。我们的期望是找到一个分裂条件，使分类后的信息熵尽可能得减小。另一常用指标还有Gini
指数：
$$G(D)=1-\sum _i{p}_i^2=1-\frac{{\sum }_i{N}_i^2}{N^2}\text{\hspace{1em}(2)}$$
Gini指数的意义表述与信息熵类似，计算过程复杂度较信息熵小。下面我们将以Gini指数为例。
对于分裂之后的Gini指数，计算公式为：
$$G=\frac{N_L}{N}G(D_L)+\frac{N_R}{N}G(D_R)\text{\hspace{1em}(3)}$$
$N_L$为左子树样本数，$N_R$为右子树样本数，$N$为总样本数，$G(D_L)$为左子样本的Gini指数，$G(D_R)$为右子样本的Gini指数。联立(2)、(3)式，可得求分裂后Gini指数的以下公式：
$$G=1-\frac{1}{N}(\frac{{\sum }_i{N}_L^2}{N_L}+\frac{{\sum }_i{N}_R^2}{N_R})\text{\hspace{1em}(4)}$$
假设特征向量$X=(x_1,x_2,...,x_i,...,x_n)$，从$x_1$开始遍历每个分量，对于其中一个特定的分量，依次用训练样本中每个$x_1$的取值作为阈值，将样本分为左右两部分，得到Gini指数最小时对应的阈值即为最佳阈值，如此可获得本节点最佳分裂所根据的分量及其最佳阈值。如此递归进行，建立决策树。

（3）叶子节点的标签

我们可以设定某些条件，如果某节点输入的样本满足这些条件，则判定不能再分裂，已经到达叶子节点(在后面剪枝以约束树的大小还会再提到)。取这些样本中众数的标签作为叶子节点的标签。

（4）终止分裂

我们需要终止分裂的条件，同时，如果树的结构过于冗杂，则会出现过拟合问题，需要通过一定的方法约束树的大小。剪枝分为预剪枝和后剪枝。预剪枝为在数生成过程中根据某些条件终止分裂，后剪枝为再构造出整棵树后将某些决策节点更改为叶子节点以缩小树的规模。
终止分裂的条件一般有样本数量小于设定最小值，树的深度大于设定最大值，信息增益(样本分列前后Gini指数之差)小于设定值等等。

三.决策树-回归

1.与分类的差异

回归树与分类树的实现过程非常相似，在递归分裂、寻找最佳阈值、依阈值分裂等步骤几乎完全相同。最大的区别在与最小化的目标（分类时为Gini指数，回归时为回归误差）以及叶子节点值的判定。

2.最佳分裂

在分类树中，Gini指数越小，样本越纯，通过最小化Gini指数使样本一步步变纯而实现分类。在回归树中，我们也要实现类似的步骤，其中衡量标准为回归误差（样本方差），每次分裂过程中，遍历特征及阈值，其中使得样本方差最小的那个分裂为最佳分裂。样本的回归误差定义为：
$$\begin{array}{rl}E(D)& =\frac{1}{l}\sum _{i=1}^l(y_i-\overline{y}{)}^2\\ & =\frac{1}{l}\sum _{i=1}^l(y_i-\frac{1}{l}\sum _{j=1}^l{y}_i{)}^2\\ & =\frac{1}{l}(\sum _{i=1}^l{y}_i^2-\frac{1}{l}(\sum _{j=1}^l{y}_j{)}^2)\end{array}\text{\hspace{1em}(5)}$$
$l$为样本总数，$y_i$为第$i$个样本的标签值。对于分裂之后的回归误差，定义为：
$$\begin{array}{r}E=\frac{N_L}{N}E(D_L)+\frac{N_R}{N}E(D_R)\end{array}\text{\hspace{1em}(6)}$$
其中$N$为左右样本数之和，$N_L$为左子树样本数，$N_R$为右子树样本数，$D_L$为分裂之后归为左子树的样本，$D_R$为右子树的样本。

3.叶子节点的标签值

在回归中，使用进入叶子节点样本标签值的均值作为改叶子节点的标签值。

四.手写决策树

1. 数据集介绍

本文对于分类任务使用鸢尾花数据集(共150条数据)，回归任务使用波士顿房价数据集(共502条数据)，这里输出查看各数据集的前5条数据：

鸢尾花数据集前5条：
其中数据为四维特征向量，代表花的四个特征，标签为0，1，2，代表三种花。

#data:
[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]]
#target:
[0 0 0 0 0]

波士顿放假数据集前5条：
其中数据为13维特征向量，标签为房价

#data:
[[6.3200e-03 1.8000e+01 2.3100e+00 0.0000e+00 5.3800e-01 6.5750e+00
  6.5200e+01 4.0900e+00 1.0000e+00 2.9600e+02 1.5300e+01 3.9690e+02
  4.9800e+00]
 [2.7310e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 6.4210e+00
  7.8900e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9690e+02
  9.1400e+00]
 [2.7290e-02 0.0000e+00 7.0700e+00 0.0000e+00 4.6900e-01 7.1850e+00
  6.1100e+01 4.9671e+00 2.0000e+00 2.4200e+02 1.7800e+01 3.9283e+02
  4.0300e+00]
 [3.2370e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 6.9980e+00
  4.5800e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9463e+02
  2.9400e+00]
 [6.9050e-02 0.0000e+00 2.1800e+00 0.0000e+00 4.5800e-01 7.1470e+00
  5.4200e+01 6.0622e+00 3.0000e+00 2.2200e+02 1.8700e+01 3.9690e+02
  5.3300e+00]]
#target:
[24.  21.6 34.7 33.4 36.2]

2. 实现过程

（1）加载库

import pandas as pd
import numpy as np
from sklearn.datasets import load_boston,load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

（2）决策树主体——节点

class Node: #节点
    min_samples_split = None #最小分裂样本数
    dim = None #维度
    max_depth = None #最大深度
    class_type = None #类型，决策树或分类树
    def __init__(self,vectors,labels,depth): #初始化时即训练
        #若样本数小于设定的最小值或者深度大于最大值，则停止分裂，到达叶子节点
        if len(vectors) <= self.min_samples_split or depth>=self.max_depth:
            self.kind = 'leaf'
            self.result = self.get_result(labels) #本叶子节点的结果（分类时为众数的标签，回归时为样本均值）
        else:
            #最小化的目标(分类时为Gini指数，回归时为回归误差)
            self.target = self.target_tobe_mined([np.array([]),labels])
            self.threshold = None #分裂阈值
            vectors_T = vectors.T
            child_target = None #分裂后的最小化指标（分类时为Gini指数，回归时为回归误差）
            I = 0
            for i in range(self.dim): #遍历特征，寻找最佳分裂特征
                for pos_thr in set(vectors_T[i]): # 遍历，寻找该特征下最佳分裂阈值
                    left_bools = vectors[:,i]<=pos_thr
                    right_bools = ~left_bools
                    left_vecs = vectors[left_bools] #左样本
                    right_vecs = vectors[right_bools]
                    left_labels = labels[left_bools] #左样本的标签
                    right_labels = labels[right_bools]
                    if len(left_labels) == 0 or len(right_labels) == 0: #某个子节点的样本数量为0
                        temp_target = self.target
                    else:
                        temp_target = self.target_tobe_mined([left_labels,right_labels])
                    if self.threshold == None or temp_target<child_target: #最小化目标
                        child_target = temp_target
                        self.threshold = pos_thr
                        self.I = i #本节点选取的特征向量的分量
                        self.l_vecs = left_vecs #左节点样本
                        self.l_labels = left_labels
                        self.r_vecs = right_vecs #右节点样本
                        self.r_labels = right_labels
            if self.target==child_target: #没有信息增益（分裂的两部分样本中有一方为空），停止分裂，则本节点判定为叶子节点
                self.kind = 'leaf'
                self.result = self.get_result(labels)
            else: #否则判定为普通节点，递归建立子树
                self.kind = 'node'
                self.l_node = Node(self.l_vecs,self.l_labels,depth+1) #左子树
                self.r_node = Node(self.r_vecs,self.r_labels,depth+1) #右子树

    def target_tobe_mined(self,value): #计算最小化指标
        N_l = len(value[0])
        N_r = len(value[1])
        if self.class_type == 'Ciassification': #分类时，返回Gini指数
            if N_l==0 or N_r==0:
                return 1-1/(N_l+N_r)*((pd.value_counts(value[0])**2).sum()/(N_l+N_r)+
                                        (pd.value_counts(value[1])**2).sum()/(N_r+N_l)) #Gini指数
            else:
                return 1-1/(N_l+N_r)*((pd.value_counts(value[0])**2).sum()/N_l+
                                        (pd.value_counts(value[1])**2).sum()/N_r)#分裂的Gini指数
        else: #回归时，回归误差（样本方差）
            if N_l==0 or N_r==0:
                return 1/(N_l+N_r)*((value[0]**2).sum()-1/(N_l+N_r)*value[0].sum()**2)+1/(N_l+N_r)*(
                                                    (value[1]**2).sum()-1/(N_l+N_r)*value[1].sum()**2)
            else:
                return 1/(N_l+N_r)*((value[0]**2).sum()-1/N_l*value[0].sum()**2)+1/(N_l+N_r)*(
                                                    (value[1]**2).sum()-1/N_r*value[1].sum()**2)
  
    def get_result(self,value): #获取叶子节点的标签（值）
        if self.class_type == 'Ciassification':
            return pd.value_counts(value).index[0] #分类时返回样本中数量最多的种类的标签
        else:
            return np.mean(value) #回归时返回样本均值

    def decide(self,vector): #分类
        if self.kind == 'leaf': #如果是叶子节点直接返回标签
            return self.result
        else: #如果不是叶子节点，根据特征进入子树
            if vector[self.I]<=self.threshold:
                return self.l_node.decide(vector)
            else:
                return self.r_node.decide(vector)

（3）建立分类与回归树

class Ciassification_And_Regression_DT: #分类与回归树
    def __init__(self,vectors,labels,min_samples_split,max_depth,kind):#根据不同的任务建立不同类型的决策树(分类或回归)
        Node.min_samples_split = min_samples_split
        Node.max_depth = max_depth
        Node.dim=len(vectors[0])
        Node.class_type = kind #树的类型
        self.decision_tree = Node(vectors,labels,0)
    def classify(self,test_x,test_y):
        results = [] #分类结果
        for i in test_x:
            res = self.decision_tree.decide(i)
            results.append(res)
        accuracy = accuracy_score(test_y,results) #正确判断的数目除以总数得准确度
        print('准确度：%.6f'%accuracy)
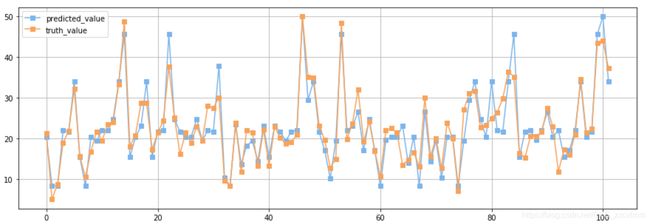
    def regress(self,test_x,test_y):
        results = [] #回归结果
        for i in test_x:
            res = self.decision_tree.decide(i)
            results.append(res)
        df = pd.DataFrame({'predicted_value':results,'truth_value':test_y})
        ave_error = abs((results-test_y)/test_y).mean()
        print('平均相对误差：%s'%ave_error)
        df.plot.line(figsize=(15,5),marker='s',color=['#7cb5ec','#f7a35c'],grid=True)

（4）分类测试

iris = load_iris() #鸢尾花数据集
train_x,test_x, train_y, test_y=train_test_split(iris.data,iris.target,test_size=0.2)

dt_classifier = Ciassification_And_Regression_DT(train_x,train_y,7,5,'Ciassification')
dt_classifier.classify(test_x,test_y)

输出结果为：

准确度：0.933333

（5）回归测试

boston = load_boston() #波士顿房价数据集
train_x,test_x, train_y, test_y=train_test_split(boston.data,boston.target,test_size=0.2)

dt_regresser = Ciassification_And_Regression_DT(train_x,train_y,13,8,'regression')
dt_regresser.regress(test_x,test_y)

输出结果为：

平均相对误差：0.12319753684552887

（橙色为真值，蓝色为预测值）