Python, Cython绘制美妙绝伦的Mandelbrot集, 曼德博集分形图案
上世纪60-70年代,美籍数学家曼德博 - Benoit B. Mandelbrot几乎单枪匹马的创立了一个新的数学分支,即分形几何学 - fractal geometry。这个新的数学分支有助于人类探索物理现象背后的数学规律,分形混沌之旋风,横扫数学、理化、生物、大气、海洋以至社会学科,在音乐、美术领域也产生了一定的影响。
分形艺术 - fractal art不同于普通的电脑绘画,它利用分形几何学和计算机强大的运算能力,将数学公式反复迭代运算,再结合作者的审美及艺术性的塑造,从而将抽象神秘的数学公式变成一幅幅精美绝伦的艺术画作。
版权声明
本文可以在互联网上自由转载,但必须:注明出处(作者:海洋饼干叔叔)并包含指向本页面的链接。
本文不可以以纸质出版为目的进行改编、摘抄。
本文节选自作者的《Python编程基础及应用》视频教程。
1. Mandelbrot集
1.1 定义
说明:阅读Mandelbrot集相关内容需要一点复数及复平面的知识,缺乏相关背景知识的读者可以略过,不影响后续内容的理解。
Mandelbrot(曼德布洛特)集是在复平面上构成分形图案的点的集合。它可以用下述复二次多项式定义:
f c ( z ) = z 2 + c f_{c}(z)=z^{2}+c fc(z)=z2+c
这里的c = x + yi是一个复数,如果把实部x和虚部y视为复平面上的横纵坐标的话,那么c对应该复平面上的一个点。从z=0开始,反复应用上述二次多项式进行迭代计算,z值将不断变化,其或者延伸至无限大,或者停留在有限半径的圆内部。如果是后者,我们称参数c导致了不发散的迭代z序列,此时,c点属于Mandelbrot集合,否则不属于。
1.2 计算
计算机显然没有办法进行无穷尽的计算才确认c所导致的迭代z值是否发散,所以我们简单地计算c点的逃逸时间 - 也就是经过多少轮迭代计算,z值的模超过2。在绘图过程中,该逃逸时间将作为c点在平面上的颜色。
def getEscapeTime(c):
"计算参数c的逃逸时间,该逃逸时间将用作点的颜色"
z = 0
for i in range(100):
if abs(z) > 2:
return i
z = z*z + c
return i
如代码所示,abs(z)用于计算复数的模,在该代码中,逃逸时间最大为100-1 = 99。同时,应注意到,Python原生支持复数运算,z*z + c就是在复数之间的运算,其代码与普通实数间的运算没有什么不同。
接下来,就可以计算Mandelbrot集合了。广义的Mandelbrot集合是个无穷大的复平面,显然,我们只可能画其中一小块。下述代码计算以(xCenter,yCenter)为中心点,semiWidth为半宽的正方形区域内的Mandelbrot集。这个正方形区域x坐标范围为xCenter±semiWidth,y坐标范围为yCenter±semiWidth。考虑到计算机只能计算离散点,所以该正方形区域将被分成N*N个点进行计算。当N=600时,下述函数的结果矩阵就是一个600x600的图像,矩形元素值代表该点的颜色。
import numpy as np
def computeMandelbrot(xCenter,yCenter,semiWidth,N):
xFrom,xTo,yFrom,yTo = xCenter-semiWidth,xCenter+semiWidth,\
yCenter-semiWidth,yCenter+semiWidth
y,x = np.ogrid[yFrom:yTo:N*1j,xFrom:xTo:N*1j]
c = x + y*1j
print("c.shape:",c.shape,"x.shape:",x.shape,"y.shape:",y.shape)
return np.frompyfunc(getEscapeTime,1,1)(c).astype(np.float)
上述代码的理解并不容易,需要先从多维数据np.ndarray的广播运算开始。对于复杂的问题,做一点小规模的模拟运算可以帮助理解。
import numpy as np
y,x = np.ogrid[1:4:4j,1:3:3j]
print("y=")
print(y)
print("x=",x)
print("shape of y:",y.shape,"shape of x:",x.shape)
执行如果如下:
y=
[[1.]
[2.]
[3.]
[4.]]
x= [[1. 2. 3.]]
shape of y: (4, 1) shape of x: (1, 3)
np.ogrid是一个特殊对象,它使用切片元组作为下标,专门用于生成用来广播的数组。1:4:4j有点类似于np.linspace(1,4,4),用于生成从1到4(含4)的有4个元素的等差数列,这里的j并不表示复数,只是一种表达形式。可以看到,ogrid生成的y是一个4行1列的二维数组,x则是一个1行3列的二维数组。其值见上。
z = y*1j
print("z = y*1j =",z)
执行结果:
z = y*1j = [[0.+1.j]
[0.+2.j]
[0.+3.j]
[0.+4.j]]
y*1j是把复数1j同y里的每一个元素相乘,并返回相同形状(维度)的数组。由于numpy模块并不是Python的原生内容,所以这里的*号并不是普通意义的Python乘法,它事实上是一个被重载的操作符函数,这个函数位于numpy模块,是用C语言书写的。可见,y*1j的结果元素的实部全是0,虚部则等于原元素值乘以1j。
再来看看x + z会得到什么,注意这里的z就是y*1j的结果。
c = x + z
print(c)
print("shape of c:",c.shape)
执行结果:
[[1.+1.j 2.+1.j 3.+1.j]
[1.+2.j 2.+2.j 3.+2.j]
[1.+3.j 2.+3.j 3.+3.j]
[1.+4.j 2.+4.j 3.+4.j]]
shape of c: (4, 3)
x是一个1行3列的二维数组,z = y*1j是一个4行1列的二维数组。两者相加事实上也是实际的被重载的numpy模块内的操作符函数,该函数将两个数组的对应元素相加。问题来了,两个数组的形状/维度不同,如何确定元素间的对应性呢? numpy进行了所谓“广播”运算,结果数组c将取x,z的各轴的最大值,其结果维度为(4,3)也就是4行3列。对于c的各个元素,比如c[3][2]为例,其值应等于x[3][2] + z[3][2],由于x[3][2]并不存在,广播规则取x[0][2] = 3代替;同样地,z[3][2]也不存在,广播规则取z[3][0] = 0. + 4.j代替;所以,c[3][2] = 3 + 0. + 4.j = 3. + 4.j。请注意,结果元素的实部来自于x数组,虚部来自于z数组,也就是y*1j的结果数组。
这里所述的“广播规则”是指当输入数组的某个轴的长度为1时,取值时均取该轴的下标0值。比如x[3][2],由于x数组的0轴长度为1,故x[3][2]的0轴下标改取0,即x[0][2]。
请读者再次观察c数组内的复数,把它看作一幅图像,从上向下,虚部的值在等差递增;从左向右,实部的值在等差递增。
xFrom,xTo,yFrom,yTo = xCenter-semiWidth,xCenter+semiWidth,\
yCenter-semiWidth,yCenter+semiWidth
y,x = np.ogrid[yFrom:yTo:N*1j,xFrom:xTo:N*1j]
c = x + y*1j
现在这段程序容易理解了,它使用与上述解读过程相同的方法把以(xCenter,yCenter)为中心点,semiWidth为半径的复平面正方形区域等分成了N行N列,多维数组c的维度即为(N,N)。c中的元素为复数,其实部在xFrom至xTo之间等差横向变化,其虚部在yFrom至yTo间等差纵向变化。
再来看函数最后一行代码:
return np.frompyfunc(getEscapeTime,1,1)(c).astype(np.float)
getEscapeTime©是之前已经定义好的一个Python语言函数,它接受一个复数参数c并计算返回这个复数参数对应的逃逸时间。np.frompyfunc()函数将二维数组c中的复数元素逐一交给getEscapeTime()进行计算,得到一个与c形状相同的结果数组。c里有多少个元素,getEscapeTime()函数就会执行多少次。执行这个结果数组的astype函数将结果数组中的元素全部转换成np.float类型。上述参数1,1表示getEscapeTime()函数接受1个参数,返回1个结果元素。
综上,computeMandelbrot()函数最后返回了一个N行N列的二维数组,数组元素为np.float类型,表明了该点的逃逸时间;而元素所在的行列编号则间接表示了元素点在结果图像/复平面中的坐标。
1.3 绘图
我们使用matplotlib绘制了Mandelbrot集的局部。左图的中心点c = 0.27322626 + 0.595153338j, 正方形半宽为0.2;右图的中心点与左图相同,半宽为0.23,相当于把左图放大了25倍。
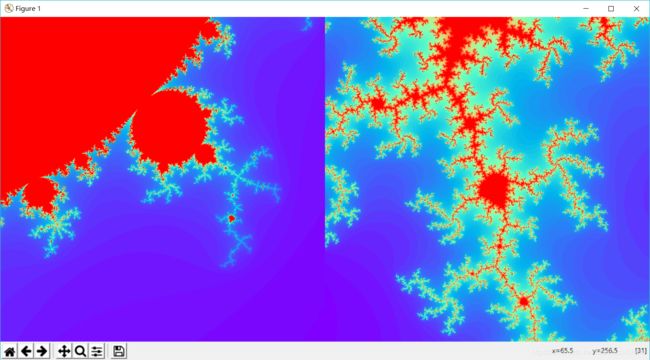
接下来分析代码。
from matplotlib import cm
...
def drawMandelbrot(ax,xCenter,yCenter,semiWidth,N,cmap):
"(xCenter,yCenter)-中心点,semiWidth-矩形半宽,N*N像素."
ax.set_axis_off()
ds = computeMandelbrot(xCenter,yCenter,semiWidth,N)
ax.imshow(ds,cmap=cmap) #在子图-ax上绘制图像,ds是计算而得的二维数组,其元素为逃逸时间
def refresh():
c = cm.get_cmap(para.cmaps[para.idxColorMap%len(para.cmaps)])
drawMandelbrot(para.ax0, para.x, para.y,
semiWidth=0.2, N=600,cmap=c)
drawMandelbrot(para.ax1, para.x, para.y,
semiWidth=0.2 ** 3, N=600,cmap=c)
para.fig.canvas.draw() #要求图-Fig重绘
pyplot中的图称为figure,图内包含一个或者多个子图-axes。drawMandelbrot()函数负责在子图上计算并画出Mandelbrot集图像。ax.set_axis_off()隐藏了子图的坐标,然后计算得到N*N像素的结果图像数组ds,接着使用ax.imshow()函数将ds在子图上画出来。该函数将ds二维数据视为一幅二维图像,ds内的每一个元素则对应图像中的一个像素点。imshow()函数内的cmap函数对应一个颜色映射对象,该对象负责把元素的值(就是复数c的逃逸时间)转换成对应的颜色。
refresh()函数则两次调用drawMandelbrot()函数画出左子图-ax0和右子图-ax1。注意,两次绘图的中心点坐标是一样的,区别是半宽不同,一个是0.2,一个是0.23。matplotlib中的cm负责管理颜色映射对象,通过cm.get_cmap()函数可以通过字符串类型的名称比如’rainbow’获得对应的颜色映射对象。para.fig.canvas.draw()函数则通知图/fig重绘。这里,我们看到一个名为para的对象,下述代码做出了解释。
from matplotlib import pyplot as plt
...
#操作者通过按上下箭头改变图像描绘颜色
def on_key_release(event): #按键松开勾子函数
if event.key == 'up':
para.idxColorMap+=1
elif event.key == 'down':
para.idxColorMap-=1
else:
return
refresh()
class Para: #一个仅有名字的Para类用于存储全局参数
pass
para = Para()
para.x, para.y = 0.27322626, 0.595153338
para.idxColorMap = 0
para.cmaps = ['flag', 'prism', 'ocean', 'gist_earth', 'terrain', 'gist_stern',
'gnuplot', 'gnuplot2', 'CMRmap', 'cubehelix', 'brg','gist_rainbow',
'rainbow', 'jet', 'nipy_spectral', 'gist_ncar']
para.fig = plt.figure(figsize=(12,6),dpi=100)
para.fig.canvas.mpl_connect('key_release_event',on_key_release)
plt.subplots_adjust(0,0,1,1,0.0,0)
para.ax0 = plt.subplot(121)
para.ax1 = plt.subplot(122)
refresh()
plt.show()
考虑到阅读本章的读者可能并不具备面向对象程序设计的知识背景,所以本章尽量避免自定义类。但作者又非常不喜欢数量过多的全局变量。作者定义了一个仅有名字的Para类并实例化了一个para对象,其中将存储那里跨函数被使用的“全局”变量。这样,理论上,全部变量只有一个,那就是para。
plt.figure()函数创建了一个长12英寸,宽6英寸的图-figure,注意dpi/每英寸点数被设定为100,这意味着图长1200像素,宽600像素。
para.fig.canvas.mpl_connect()函数将按键弹起事件与on_key_release()函数相关联,即图-figure处于活动状态时,操作者按下一个键并松开时,on_key_release(event)函数将被执行,event参数包括了事件的相关信息:比如事件的类型,哪个键被松开等等。这个on_key_release()函数与特定事件相绑定,俗称“勾子函数” - hook function。
plt.subplots_adjust()函数调整了子图间的间距和边距,使得整个显示窗口被充分利用。
plt.subplot(121)在当前图-figure对象内创建了一个子图-axes,并存于para.ax0。121参数被该函数以非常特别的方式处理,它表示将当前图的可见区域分成1行2列,在其中1号位置创建一个子图,即结果中的左子图。同理,plt.subplot(122)将当前图的可见区域分成1行2列,在其中2号位置创建一个子图,即结果中的右子图。
refresh()函数将计算并画出两个子图。plt.show()则把窗口显示出来。
接下来,我们研究一下勾子函数on_key_release(event)。这个函数使得操作者按上下箭头可以改变当前图像颜色并重绘。para.cmaps列表存储了一系列可用的映射对象的名称,para.idxColorMap则记录了当前使用的映射对象在para.cmaps列表中的下标。on_key_release(event)函数判断event对应的按键类型,如果是up,para.idxColorMap+1,如果是down, para.idxColorMap-1。on_key_release()函数通过调用refresh()函数再实现图的重绘,在refresh函数内部,para.idxColorMap以len(para.cmaps)取模后再使用。这是因为,para.idxColorMap的加减没有进行越界检查,para.idxColorMap可能为负数,也可能为超过para.cmaps长度的正数,取模可以保证获得合法的下标。
需要提醒读者的是,一幅子图有600*600 = 36万个像素,两幅子图有72万个像素。每个像素的计算都会调用一次getEscapeTime()函数,而这个函数是Python语言写的,并且里面要进行不超过100次的循环运算,执行速度很慢。所以读者运行出界面后,按上下箭头时不要太心急,按一下后要等刷新结束再按下一次。
2. Cython加速Mandelbrot集
用纯Python语言写就的Mandelbrot集绘图程序速度太慢了! 但Python是所谓的胶水语言,可以很方便地通过C或者其它语言来书写扩展库,numpy, scipy, matploblib都是这些扩展库的杰出代表。
至少有两个途径可以加速Mandelbrot集的计算速度。方法1是直接用C语言书写计算逃逸时间的函数,然后使用mingw、g++或者Visual C++编译器将其编译成目标模块,然后在Python语言里调用。这非常麻烦,因为函数的参数需要手工解析,还需要记忆和使用大量的Python API。
方法2则是Cython。Cython在语法上基本与Python相同,同时又允许直接定义和调用C语言函数、定义变量类型等功能。Cython的编译器会把Cython的源程序编译成C语言程序,再经由C语言编译器编译成Python模块。由于Python解释器本身也是由C语言写就,并经由C语言编译器编译的,所以Cython里可以很方便地访问Python类型对象。
2.1 环境准备
世界发展得太快,当读者阅读本书时,下述信息或许已经过时。
作者使用的是Windows 10环境下的64位的Python3.7解释器, 所以作者安装了微软的Visual Studio社区版的"使用C++的桌面开发"部分,其中包括了VC 2017 version 15.9 v14.16以及相关的Windows SDK。该软件可以从 https://visualstudio.microsoft.com 获得。请注意,Visual Studio是一个非常宠大的IDE软件,除上述必要部分之外的请不要选择,否则非常耗时而且占据硬盘空间。
如果读者使用的是Linux, 则系统自带的gcc编译通常足够使用。Linux下Cython代码的编译过程与下述过程相当,但细节或有区别。
读者还需要安装Cython模块,在Windows命令行或者Linux终端中运行pip install cython即可。
2.2 重写逃逸时间计算函数
在PyCharm中新建一个文件(New->File),命名为MandelbrotComp.pyx。其内为Cython代码:
def getEscapeTime(complex c):
"计算参数c的逃逸时间,该逃逸速度将用作点的颜色"
cdef complex z = 0
cdef int i
for i in range(255):
if z.real * z.real + z.imag*z.imag > 4:
return i
z = z*z + c
return i
可以看到,上述代码与之前纯Python写的getEscapeTime()函数主要有如下的不同:
首先,所有的变量/对象都有类型声明,大部分通过cdef关键字定义。c,z的类型为complex,i的类型为int。强类型是C/C++的特点,也是C/C++可以编译出高效机器码的必要条件。
第二,我们没有再使用abs来计算复数z的模,这可能有两个原因:1). 原生C语言没有用于复数求模的abs()函数,沿用abs()函数很可能会导致该模块再次内部调用Python的abs()函数;2). 复数的求模运算需要求平方根,而平方根的求解运算代价较高。而且,平方根的求解在此处是不必要的,我们直接求z的实部和虚部的平方之和,再比较其是否大于4事实上等价于比较z的模是否大于2。
2.3 编译为扩展模块
按照Cython文档的建议,我们准备了一个setup.py文件,其内容如下:
from distutils.core import setup
from Cython.Build import cythonize
setup(name='Mandelbrot Computation',
ext_modules=cythonize("MandelbrotComp.pyx"))
请注意,setup.py与MandelbrotComp.pyx以及预期使用该扩展块的Mandelbrot绘图程序均在同一目录下。然后通过Windows开始菜单进入"适用于VS 2017的x64本机工具命令提示",通过cd命令切换至setup.py及MandelbrotComp.pyx所在目录。再执行python setup.py build_ext --inplace命令。
如下图所示,需要说明的是,下图事实上是个黑黑的终端界面,cd等命令可以追溯到40年前的DOS操作系统,也就是Windows操作系统的前身。该命令提示界面与普通Windows命令行的主要区别在于通过执行vcvarsall.bat批处理命令, 该界面内对环境变量Path进行了临时设置,以确保VC编译器-cl.exe,以及相关的C语言头文件,库文件可以被找到。读者不要在普通的Windows命令行下做下述工作,setup.py会报告找不到编译器或者C语言头文件。
适用于VS2017的x64本机工具命令提示
**********************************************************************
** Visual Studio 2017 Developer Command Prompt v15.9.4
** Copyright (c) 2017 Microsoft Corporation
**********************************************************************
[vcvarsall.bat] Environment initialized for: 'x64'
C:\Program Files (x86)\Microsoft Visual Studio\2017\Community>d:
D:\>cd Python
D:\Python>cd MathBeauty
D:\Python\MathBeauty>python setup.py build_ext --inplace
一切顺利的话,上述命令将报告“已完成代码的生成”。此时,可以在PyCharm里看到代码目录下多出来两个文件,其中一个名为MandelbrotComp.c。这是由Cython编译MandelbrotComp.pyx生成的C语言程序,作者抄出来一个小片段:
for (__pyx_t_1 = 0; __pyx_t_1 < 0x64; __pyx_t_1+=1) {
__pyx_v_i = __pyx_t_1;
__pyx_t_2 = ((((__Pyx_CREAL(__pyx_v_z) * __Pyx_CREAL(__pyx_v_z)) + (__Pyx_CIMAG(__pyx_v_z) * __Pyx_CIMAG(__pyx_v_z))) > 4.0) != 0);
if (__pyx_t_2) {
__Pyx_XDECREF(__pyx_r);
__pyx_t_3 = __Pyx_PyInt_From_int(__pyx_v_i); if (unlikely(!__pyx_t_3)) __PYX_ERR(0, 7, __pyx_L1_error)
__Pyx_GOTREF(__pyx_t_3);
__pyx_r = __pyx_t_3;
__pyx_t_3 = 0;
goto __pyx_L0;
}
__pyx_v_z = __Pyx_c_sum_double(__Pyx_c_prod_double(__pyx_v_z, __pyx_v_z), __pyx_v_c);
}
由于是机器“写”出来的C代码,特别难理解。作者找到了那个从0到100(不含100)的循环,0x64是十六进制,它就是十进制的100。
另外一个生成出来的文件名为MandelbrotComp.cp37-win_amd64.pyd。读者的Python版本或者操作系统如果与作者的不同,该名称或有差异。这个文件就是编译好的Python扩展模块。
2.4 调用扩展模块
from MandelbrotComp import getEscapeTime
def computeMandelbrot(xCenter,yCenter,semiWidth,N):
xFrom,xTo,yFrom,yTo = xCenter-semiWidth,xCenter+semiWidth,\
yCenter-semiWidth,yCenter+semiWidth
y,x = np.ogrid[yFrom:yTo:N*1j,xFrom:xTo:N*1j]
c = x + y*1j
print("c.shape:",c.shape,"x.shape:",x.shape,"y.shape:",y.shape)
return np.frompyfunc(getEscapeTime,1,1)(c).astype(np.float)
上述pyd文件与绘图代码在同一目录下。使用该扩展模块与使用其它模块没有什么不同。from MandelbrotComp import getEscapeTime导入了该模块并引用了函数名。np.frompyfunc()则函数则直接使用该函数对象。此时,当numpy的C程序将c二维数组中的元素逐一交给getEscapeTime()函数计算时,该函数由于是C语言编写,其执行速度有了质的提升。读者可以运行随书代码中的InteractiveMandelbrot.py,体会一下速度变化。
需要说明的是,如果读者使用的不是Windows,那么InteractiveMandelbrot.py无法直接运行。C语言的编译结果与硬件平台(Intel x86或者ARM体系结构)、操作系统等有关。在Windows下编译的机器代码是无法在Linux下直接运行的。读者需要重新编译MandelbrotComp.pyx文件为扩展模块。
2.5 交互Mandelbrot绘图
作者随书提供了一个名为InteractiveMandelbrot.py的文件,该绘图程序提供了交互功能。操作者除了可以使用上下箭头来改变绘图颜色之外,还可以使用鼠标的左右键来放大/缩小图像。按下Esc键,则图像还原。
para.semiWidth = 1.5
para.figWidth,para.figHeight = 700,700
para.fig.canvas.mpl_connect('button_release_event',on_button_release)
为了实现上述功能,作者在para对象增加了figWidth, figHeight以表示绘图窗口的像素宽度和高度。para.semiWidth则表明当前的绘图半宽。当该绘图半宽变小,则相当于图像被放大。
当鼠标按键被松开时,on_button_release()勾子函数被调用。
def on_button_release(event):
para.x = (para.x - para.semiWidth) + 2*para.semiWidth*event.xdata/para.figWidth
para.y = (para.y - para.semiWidth) + 2*para.semiWidth*event.ydata/para.figHeight
if event.button == 1:
para.semiWidth /= 3.0
elif event.button == 3:
para.semiWidth *= 3.0
refresh()
该函数首先借助于para.figWidth, figHeight, 鼠标点击坐标event.xdata, event.ydata等信息重新计算了新的绘图中心点para.x, para.y。
如果是鼠标左键弹起(event.button==1),则减少绘图半宽-para.semiWidth,放大图像。否则增大绘图半宽,缩小图像。refresh()函数则负责重绘,绘图中心点以及半宽从para.x, para.y, para.semiWidth取值。
def on_key_release(event):
if event.key == 'up':
para.idxColorMap+=1
elif event.key == 'down':
para.idxColorMap-=1
elif event.key == 'escape':
para.x, para.y = -0.5, 0.0
para.semiWidth = 1.5
else:
return
refresh()
在on_key_release()勾子函数内,'escape’键弹起时,恢复para.x, para.y, para.semiWidth的初值并重绘,图像还原成初始状态。
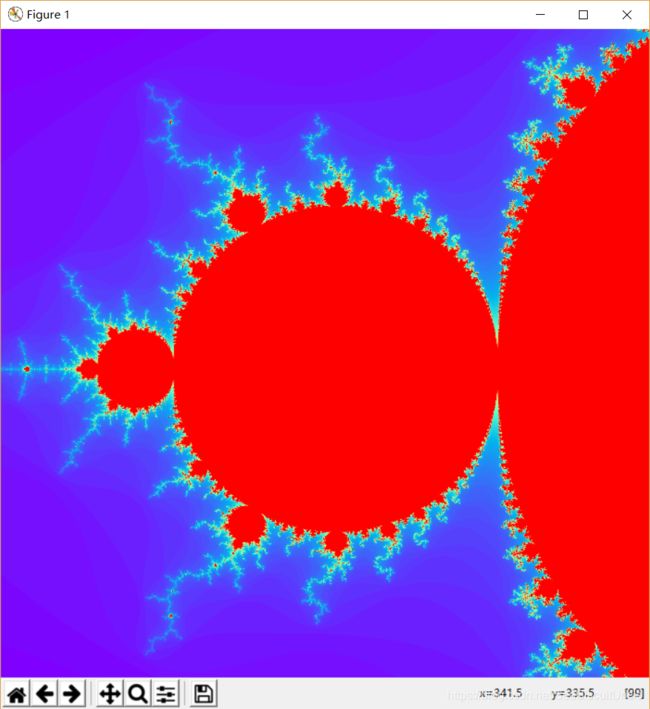
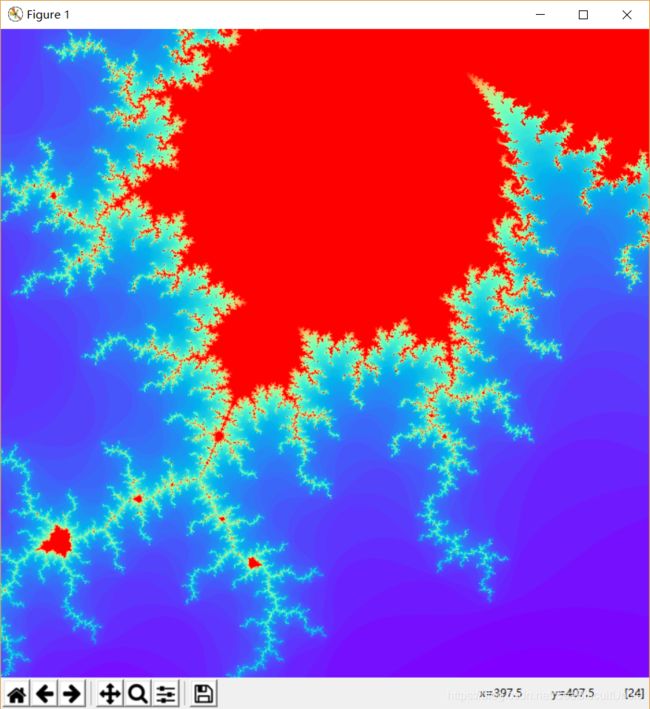
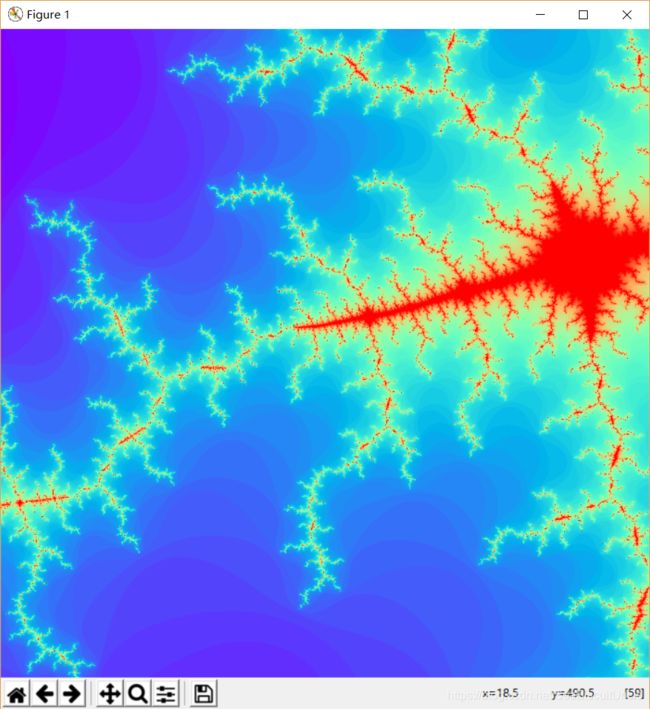
下面是中心点为(-0.5, 0.0),半宽为1.5的“全局”图像(图1)以及不同轮次放大的局部图像。
 |
 |
|---|---|
 |
 |
本文节选自作者的《Python编程基础及应用》视频教程。想完整零基础学习Python程序设计,欢迎使用此免费视频教程。