A*寻路算法之解决路径多拐点问题

1.问题描述

最近公司正在开发的游戏涉及到了寻路算法，然后我从网上找了一份A*算法代码，整理了一下写了一个A*算法基础实现。然而，在真正实用时A*寻路时，却发现了几个问题：

1. 基础实现版的A*寻路算法在大地图的搜索上，耗时较长；

2. 使用最小堆实现的OpenList来优化A*算法后，发现最后得到的路径往往是S型的；

然后策划看到效果后，提出了两点要求：1）寻路的路径中，拐点必须最少；2）存在多条路径时，必须优先走最快碰到拐点的路径。

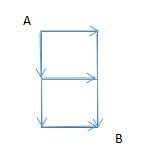
稍微解释一下上面的两个需求：假如出发点和目的点是"日"字型时，可经过上中下三条路径到达目的地。上下两条路径的拐点是1个，而中间路径的拐点是2个，淘汰中间路径。另外，上路走一步碰到拐点，而下路走两步碰到拐点，那么优先选择上路。

2. A*算法基本实现及优化

假设看这篇文章的朋友，都是已经了解A*算法的。如果还不了解A*算法，可以先百度一下，网上介绍A*算法的文章很多。

从网上找了一个A*算法的JAVA版实现，经过整理后实现如下：

public class AStar {

	/** 地图 */
	private GameMap map;
	private ArrayList openList = new ArrayList<>();
	private ArrayList closeList = new ArrayList<>();

	public AStar(GameMap map) {
		this.map = map;
	}
	
	public Node findPath(Node startNode, Node endNode) {
		// 把起点加入 open list
		openList.add(startNode);
		
		while (openList.size() > 0) {
			// 遍历 open list ，查找 F值最小的节点，把它作为当前要处理的节点
			Node currNode = findMinFNodeInOpenList();
			// 从open list中移除
			openList.remove(currNode);
			// 把这个节点移到 close list
			closeList.add(currNode);
			
			// 查找最小FCost的节点
			ArrayList neighborNodes = findNeighborNodes(currNode);
			for (Node nextNode : neighborNodes) {
				int gCost = calcNodeCost(currNode, nextNode) + currNode.gCost;
				if (exists(openList, nextNode)) {
					// 如果新的路径fCost更小，更新nextNode节点
					if (gCost < nextNode.gCost) {
						nextNode.parent = currNode;
						nextNode.gCost = gCost;
						nextNode.fCost = nextNode.gCost + nextNode.hCost;
					}
				} else {
					// 计算nextNode节点的fCost
					nextNode.parent = currNode;
					nextNode.gCost = gCost;
					nextNode.hCost = calcNodeCost(nextNode, endNode);
					nextNode.fCost = nextNode.gCost + nextNode.hCost;
					openList.add(nextNode);
				}
			}
			
			Node node = find(openList, endNode);
			if (node != null) {
				return node;
			}
		}

		return find(openList, endNode);
	}
	
	public Node findMinFNodeInOpenList() {
		Node tempNode = openList.get(0);
		for (Node node : openList) {
			if (node.fCost < tempNode.fCost) {
				tempNode = node;
			}
		}
		return tempNode;
	}

	public ArrayList findNeighborNodes(Node currentNode) {
		ArrayList arrayList = new ArrayList();
		addNode(arrayList, currentNode.x, currentNode.y - 1);
		addNode(arrayList, currentNode.x, currentNode.y + 1);
		addNode(arrayList, currentNode.x - 1, currentNode.y);
		addNode(arrayList, currentNode.x + 1, currentNode.y);
		return arrayList;
	}

	private void addNode(ArrayList arrayList, int x, int y) {
		if (map.canReach(x, y) && !exists(closeList, x, y)) {
			arrayList.add(new Node(x, y));
		}
	}
	
	private int calcNodeCost(Node node1, Node node2) {
		return abs(node2.x - node1.x) + abs(node2.y - node1.y);
	}
	
	public int abs(final int x) {
		final int i = x >>> 31;
		return (x ^ (~i + 1)) + i;
	}

	public static Node find(List nodes, Node point) {
		for (Node n : nodes)
			if ((n.x == point.x) && (n.y == point.y)) {
				return n;
			}
		return null;
	}
	
	public static boolean exists(List nodes, Node node) {
		for (Node n : nodes) {
			if ((n.x == node.x) && (n.y == node.y)) {
				return true;
			}
		}
		return false;
	}

	public static boolean exists(List nodes, int x, int y) {
		for (Node n : nodes) {
			if ((n.x == x) && (n.y == y)) {
				return true;
			}
		}
		return false;
	}
}

上面的代码实现了A*算法的逻辑，但是在200*200的地图上测试时，从(0,0)点走到(199,199)寻路一次通常要几秒到十几秒。

那么，我们先分析一下代码的性能为什么那么低。主要有两点：

1)  findMinFNodeInOpenList() 方法需要遍历 open list ，查找 F值最小的节点，该方法的时间复杂度是O(n)。虽然该方法时间复杂度是线性的，但是每次检查一个节点时，都会执行一次该方法。

2） 添加新节点或者更新下一个节点时，都会调用一次exists()方法判断节点是否在openList或者closeList中。该方法同样是线性的，但是添加新节点或者更新下一个节点时,总会调用一次或多次，因此时间复杂度是m*O(n)。

针对上面两个痛点进行优化：首先，在一个队列中获取获取最大/最小的元素，我们通常首先想到的就是最大/小堆，因此，利用优先队列PriorityQueue实现openList，那么每次从openList中查找 最小F值的节点时，时间复杂度将降为O(lg n)。其次，分析上下文发现，closeList仅在添加节点到openList时做去重判断，而没有其他作用，那么可以通过数组标记或者Map存储遍历信息，使时间复杂度达到O(1)。以下是优化后的代码：

public class AStarOptimization {
	
	/** 地图 */
	private GameMap map;
	
	private PriorityQueue newOpenList = new PriorityQueue<>(new Comparator() {

		@Override
		public int compare(Node o1, Node o2) {
			return o1.fCost - o2.fCost;
		}
		
	});
	
	private Set openSet = new HashSet<>();
	private Set closeSet = new HashSet<>();
	
	public AStarOptimization(GameMap map) {
		this.map = map;
	}
	
	public List findPath() {
		return findPath(map.getStartNode(), map.getEndNode());
	}
	
	public List findPath(Node startNode, Node endNode) {
		newOpenList.add(startNode);

		Node currNode = null;
		while ((currNode = newOpenList.poll()) != null) {
			removeKey(openSet, currNode.x, currNode.y);
			addKey(closeSet, currNode.x, currNode.y);

			ArrayList neighborNodes = findNeighborNodes(currNode);
			for (Node nextNode : neighborNodes) {
				int gCost = calcNodeCost(currNode, nextNode) + currNode.gCost;
				if (contains(openSet, nextNode.x, nextNode.y)) {
					if (gCost < nextNode.gCost) {
						nextNode.parent = currNode;
						nextNode.gCost = gCost;
						nextNode.fCost = nextNode.gCost + nextNode.hCost;
					}
				} else {
					nextNode.parent = currNode;
					nextNode.gCost = gCost;
					nextNode.hCost = calcNodeCost(nextNode, endNode);
					nextNode.fCost = nextNode.gCost + nextNode.hCost;
					newOpenList.add(nextNode);
					
					addKey(openSet, nextNode.x, nextNode.y);
				}
			}
			
			if (contains(openSet, endNode.x, endNode.y)) {
				Node node = findOpenList(newOpenList, endNode);
				return getPathList(node);
			}
		}

		Node node = findOpenList(newOpenList, endNode);
		return getPathList(node);
	}
	
	public ArrayList findNeighborNodes(Node currentNode) {
		ArrayList arrayList = new ArrayList();
		addNode(arrayList, currentNode.x, currentNode.y - 1);
		addNode(arrayList, currentNode.x, currentNode.y + 1);
		addNode(arrayList, currentNode.x - 1, currentNode.y);
		addNode(arrayList, currentNode.x + 1, currentNode.y);
		return arrayList;
	}

	private void addNode(ArrayList arrayList, int x, int y) {
		if (map.canReach(x, y) && !contains(closeSet, x, y)) {
			arrayList.add(new Node(x, y));
		}
	}

	private int calcNodeCost(Node node1, Node node2) {
		return abs(node2.x - node1.x) + abs(node2.y - node1.y);
	}
	
	private Node findOpenList(PriorityQueue nodes, Node point) {
		for (Node n : nodes) {
			if ((n.x == point.x) && (n.y == point.y)) {
				return n;
			}
		}
		return null;
	}
	
	public List getPathList(Node parent) {
		List list = new ArrayList<>();
		while (parent != null) {
			list.add(new Node(parent.x, parent.y));
			parent = parent.parent;
		}
		return list;
	}
	
	public int abs(final int x) {
		final int i = x >>> 31;
        return (x ^ (~i + 1)) + i;
	}
	
	private void addKey(Set set, int x, int y) {
		set.add(getKey(x, y));
	}
	
	private void removeKey(Set set, int x, int y) {
		set.remove(getKey(x, y));
	}
	
	private boolean contains(Set set, int x, int y) {
		return set.contains(getKey(x, y));
	}
	
	private String getKey(int x, int y) {
		StringBuilder sb = new StringBuilder();
		sb.append(x).append('_').append(y);
		return sb.toString();
	}
	
}

优化后的代码在200*200的地图上测试，在障碍物比例为0.3时（200 * 200 * 0.3），从(0,0)点走到(199,199)寻路一次基本在30ms~50ms。

3. 多拐点问题

由于基于最小堆实现的优先队列是不稳定，在多个具有相同F值的节点中选择最小节点的顺序是无法保证的。因此，以上优化后的代码走出来的路径通常都是S型的，也就是存在拐点过多的问题。

是否使用基础版本的A*算法是否可以消除多拐点的问题呢？答案是否定的，基础版本的A*算法是按照一定的方向顺序添加节点，在相同F值时，获取节点也是按照相同方向顺序获取节点，这在空旷的地形中是不会出现S型路径。但是，当路径上有障碍物时，按照顺序添加节点然后按照顺序取节点的方法，就会出现走S型路径的问题。

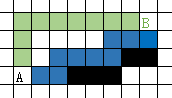
例如，如图所示情形，当从A点出发移动到B， A*算法按照上下左右的方向顺序添加节点，A从绿色路径移动到B；相反，如果从B移动到A点，A*算法会向下走到A点，但是沿途有障碍物，于是就形成了S型路径。

 

那么，基于最小堆实现的openList，如何杜绝路径多拐点呢？路径是算法执行过程中动态生成，生成或有路径去选择一条是不可能。最好的办法是，根据路径的特点调整路径上拐点的F值。

A*算法是利用启发函数：F(n) = G(n) + H(n)，来确定每个点的F值，采用贪心策略选择F值最小的点作为下一个待更新节点，直到找到终点。其中G(n)表示从起始点走到该点的代价，H(n)估算从该点走到终点的代价。通常G(n)采用走到该点所用的步数来表示，而H(n)使用该点到终点的距离来表示。

从启发函数来看，A*算法对于路径的特点根本没有做任何要求，只要是最小F值的节点都可以加入路径当中。因此，我们可以在启发函数中加入对节点的路径特征的评判，使算法选择的最终结果符合我们的预期。基于此目的，修改启发函数：

F(n) = G(n) + H(n) + E(n)

其中E(n)表示加入该节点后，对路径的评分进行的微调。话不多说，先上代码：

	public List findPath(Node startNode, Node endNode) {
		newOpenList.add(startNode);

		Node currNode = null;
		while ((currNode = newOpenList.poll()) != null) {
			removeKey(openSet, currNode.x, currNode.y);
			addKey(closeSet, currNode.x, currNode.y);

			ArrayList neighborNodes = findNeighborNodes(currNode);
			for (Node nextNode : neighborNodes) {
				// G + H + E
				int gCost = 10 * calcNodeCost(currNode, nextNode) + currNode.gCost 
						+ calcNodeExtraCost(currNode, nextNode, endNode);
				if (contains(openSet, nextNode.x, nextNode.y)) {
					if (gCost < nextNode.gCost) {
						nextNode.parent = currNode;
						nextNode.gCost = gCost;
						nextNode.fCost = nextNode.gCost + nextNode.hCost;
					}
				} else {
					nextNode.parent = currNode;
					nextNode.gCost = gCost;
					nextNode.hCost = 10 * calcNodeCost(nextNode, endNode);
					nextNode.fCost = nextNode.gCost + nextNode.hCost;
					newOpenList.add(nextNode);
					
					addKey(openSet, nextNode.x, nextNode.y);
				}
			}
			
			if (contains(openSet, endNode.x, endNode.y)) {
				Node node = findOpenList(newOpenList, endNode);
				return getPathList(node);
			}
		}

		Node node = findOpenList(newOpenList, endNode);
		return getPathList(node);
	}
	
	private int calcNodeExtraCost(Node currNode, Node nextNode, Node endNode) {
		// 第一个点或直线点
		if (currNode.parent == null || nextNode.x == currNode.parent.x 
				|| nextNode.y == currNode.parent.y) {
			return 0;
		}
		
		// 拐向终点的点
		if (nextNode.x == endNode.x || nextNode.y == endNode.y) {
			return 1;
		}
		
		// 普通拐点
		return 2;
	}

代码的终点是calcNodeExtraCost()方法，方法中判断如果nextNode和之前的节点是保持直线的，那么E值为0，否则如果是一个拐点的话，E值将大于0，并且这个E值会和G值存在一起，作为新的G值。

A*路径多拐点的问题暂时写到这里了，之后再补上后面的内容。