跳转点寻路介绍
有均衡代价的2D网格上寻找最短路径有几种算法。A*算法是一种对宽度优先和深度优先搜索的常见并且简单的优化。对于这样的算法有很多扩展,包括D*、HPA*和Rectangular Symmetry Reduction,每一种都试图减少最优路径节点数量。
跳转点(Jump Point Search )寻路逻辑是由Daniel Harabor和Alban Grastien提出的,是一种使在矩形网格上寻路更加有效地方法。在这篇文章中,我将不遗余力的介绍它,但是不是研究论文中的底层数学公式。而是尝试通过图表引起你的兴趣。
我假设你已经很熟悉A*算法,甚至Dijkstra寻路。如果想要了解背景信息和更好地介绍,请查看Amit’s introduction to A*。
对于下面的例子,我假设寻路是在一个常用的方格上,水平和垂直方向的移动代价为1,对角线的移动代价为√2̅。
尝试一下
你可以演示A*和JPS。通过点击和拖拽任何地方以增加障碍,拖拽绿色(开始)和红色(目标)节点来移动它们,并且点击“Find Path"按钮来寻找最优路径。译者注:由于原文是一个网页演示,所以转载不过来,请直接去原文演示。
减少路径扩展和对称
在A*每一次迭代期间,我们在已知最好的方向上扩大搜索范围。然而,有一些情况可能会导致低效的情况出现。在大的开放的空间中会出现一种低效的情况。为了展示示例,让我们来看一个矩形网格。
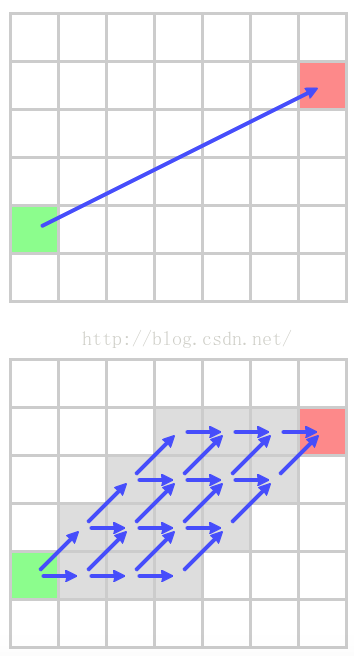
在一个开放的网格上,有一条从绿点到红点的路径。
有许多种等效的路径穿越这个矩形区域。Dijkstra's,做一个广度搜索,是一个不错的例证。你会发现,每一条路的代价是相同的。唯一的不同是我们选择对角还是水平行走。
在这片研究文章中,Harabor和Grastien把这称作“对称路径”,因为他们是完全相同的效果。理想情况下,我们应该识别这种情况,并忽略其它而保留一种情况。
更智能
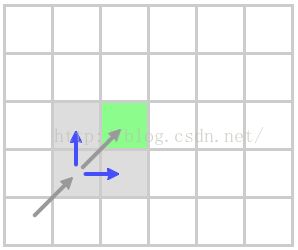
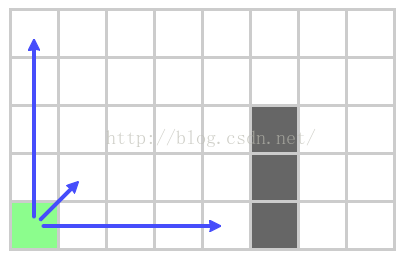
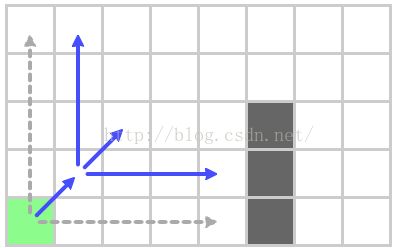
展望水平和垂直方向
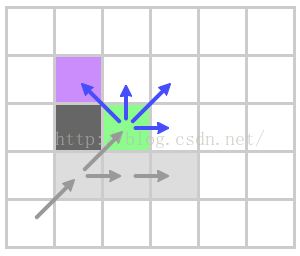
展望对角
一起试一下
在这个特别的方向行走的时候,我们已经为了一个节点跳过了大部分邻居节点,并且已经制定了一些规则跳往下一格节点。
把这个恢复到A*逻辑,我们将应用这些“jumping ahead”在open容器里的节点。我们将用它的父对象决定移动方向和向前跳到我们能到达的地方。如果我们找到一个感兴趣的节点,我们将忽略所有中间的节点(因为我们已经用我们简单的规则跳过了他们)并且把它们加到open容器里。
在open容器里的每一个节点都是根据父对象的方向扩展的,并随着前面同样地跳点:先向水平和垂直,然后对角移动。
这里是一个扩展序列的例子,在最后标记最终路径。
首先,确定一个目标。
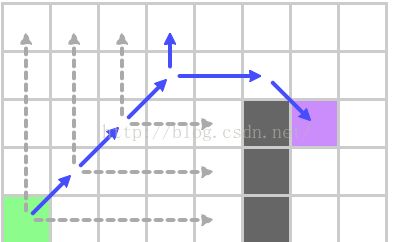
从预先设定的节点开始(open容器里的唯一一个),我们水平和垂直方向扩展寻找。
水平跳的时候找到一个强制邻居(紫色高亮的节点)。我们把它加入到open容器中。
最后,我们沿对角线扩展,除了碰到边缘,并没有找到任何东西。
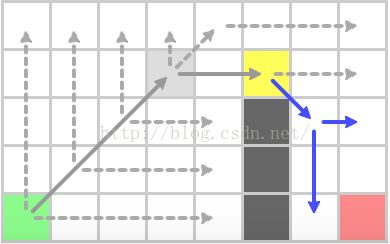
接着,我们检测下一个最优(或者仅仅是这种情况的)的open节点。因为当我们到达这个节点的时候我们正在水平移动,所以我们继续水平移动。
因为我们也遇到一个强制邻居,我们也在那个方向扩展。跟着对角线规则,我们也对角线移动,然后水平、垂直方向寻找。
没有找到任何东西,继续对角线移动。
这一次,当我们水平移动(哪都去不了)和垂直移动时,我们找到了目标节点。用强制邻居找一个节点真是非常有趣,所以我们把这个节点加入到open容器里。
最后,我们扩展最后一个open节点,找到目标。跳过算法的最后一次迭代,把目标节点加入到open容器里,我们找到了最有路径。
备注
1.代码是用于创建这些图表,并且交互式的路径寻找可以在GitHub上的jps-explained project下找到。
2.The original research paper by Daniel Harabor and Alban Grastien 正式介绍了JPS算法,并且可以作为一个优秀的参考去实现自己的算法。几篇其他相关的论文在哥哥
Mr. Harabor’s website.
3.Mr.Harabor's原创博客公布了一系列的Rectangular Symmetry Reduction和Jump Point Search,在这里
4.Amit’s A* Pages是一个优秀的介绍A*和寻路算法的博客。
5.Xueqiao Xu已经创建了一个JavaScript的寻路库,叫做PathFinding.js,其中包含了JPS,并且有一个demo,你可以直接在这里产生可视的图表。
6.我在这 project experimenting with pathfinding and visualization里应用了JPS。