C#数据结构与算法之二:线性表
目录
第二章 线性表
2.1 CLR中的线性表
2.2线性表的接口定义
2.3线性表的实现方式
2.3.1顺序表
2.3.2单链表
2.3.3双向链表
2.3.4循环链表
2.4栈和队列
2.4.1栈
2.4.2队列
2.4.3栈和队列应用实例
2.5串和数组
2.5.1串
2.5.2数组
首先感谢siki老师对C#数据结构与算法的讲解。原视频内容戳这里http://www.sikiedu.com
第二章 线性表
线性表是最简单、最基本、最常用的数据结构。线性表是线性结构的抽象(Abstract),线性结构的特点是结构中的数据元素之间存在一对一的线性关系。这种一对一的关系指的是数据元素之间的位置关系,即:(1)除第一个位置的数据元素外,其它数据元素位置的前面都只有一个数据元素;(2)除最后一个位置的数据元素外,其它数据元素位置的后面都只有一个元素。也就是说,数据元素是一个接一个的排列。因此,可以把线性表想象为一种数据元素序列的数据结构。线性表就是位置有先后关系,一个接着一个排列的数据结构。
2.1 CLR中的线性表
c# 2.0 提供了泛型的IList
2.2线性表的接口定义
namespace 线性表
{
interface IListDS
{
int GetLength();
void Clear();
bool IsEmpty();
void Add(T item);
void Insert(T item, int index);
T Delete(int index);
T this[int index] { get; }
T GetEle(int index);
int Locate(T value);
void ToString();
}
}
2.3线性表的实现方式
2.3.1顺序表
在计算机内,保存线性表最简单、最自然的方式,就是把表中的元素一个接一个地放进顺序的存储单元,这就是线性表的顺序存储(Sequence Storage)。线性表的顺序存储是指在内存中用一块地址连续的空间依次存放线性表的数据元素,用这种方式存储的线性表叫顺序表(Sequence List),如图所示。顺序表的特点是表中相邻的数据元素在内存中存储位置也相邻。
图2.3.1
假设顺序表中的每个数据元素占w个存储单元,设第i个数据元素的存储地址为Loc(ai),则有:Loc(ai)= Loc(a1)+(i-1)*w 1≤i≤n式中的Loc(a1)表示第一个数据元素a1的存储地址,也是顺序表的起始存储地址,称为顺序表的基地址(Base Address)。也就是说,只要知道顺序表的基地址和每个数据元素所占的存储单元的个数就可以求出顺序表中任何一个数据元素的存储地址。并且,由于计算顺序表中每个数据元素存储地址的时间相同,所以顺序表具有任意存取的特点。(可以在任意位置存取东西)
C#语言中的数组在内存中占用的存储空间就是一组连续的存储区域,因此,数组具有任意存取的特点。所以,数组天生具有表示顺序表的数据存储区域的特性。
namespace 线性表
{
///
/// 顺序表实现方式
///
/// : IListDS
{
private T[] data;//数据容器
private int count;//存放数据个数
public SeqList(int size)//初始化最大容量
{
data = new T[size];
count = 0;
}
public SeqList() : this(10)//默认容量为10
{
}
///
/// 通过索引得到数据
///
///
///
/// 清空表
///
public void Clear()
{
count = 0;
}
///
/// 按索引删除数据
///
///
///
/// 取得数据的个数
///
///
///
/// 取得顺序表长度
///
///
/// 按索引插入数据
///
///
///
public void Insert(T item, int index)
{
if (index >= 0 && index < count)
{
for (int i = count - 1; i >= index; i--)
{
data[i + 1] = data[i];
}
data[index] = item;
count++;
}
else
{
Console.WriteLine("索引不存在");
}
}
///
/// 判断表是否为空
///
///
/// 按值得到索引
///
///
/// seqList = new SeqList();
seqList.Add("Lemon");
seqList.Add("SS");
seqList.Add("214");
seqList.Insert("999", 2);
seqList.ToString();
Console.ReadKey();
}
}
}
2.3.2单链表
顺序表是用地址连续的存储单元顺序存储线性表中的各个数据元素,逻辑上相邻的数据元素在物理位置上也相邻。因此,在顺序表中查找任何一个位置上的数据元素非常方便,这是顺序存储的优点。但是,在对顺序表进行插入和删除时,需要通过移动数据元素来实现,影响了运行效率。线性表的另外一种存储结构——链式存储(Linked Storage),这样的线性表叫链表(Linked List)。链表不要求逻辑上相邻的数据元素在物理存储位置上也相邻,因此,在对链表进行插入和删除时不需要移动数据元素,但同时也失去了顺序表可随机存储的优点。
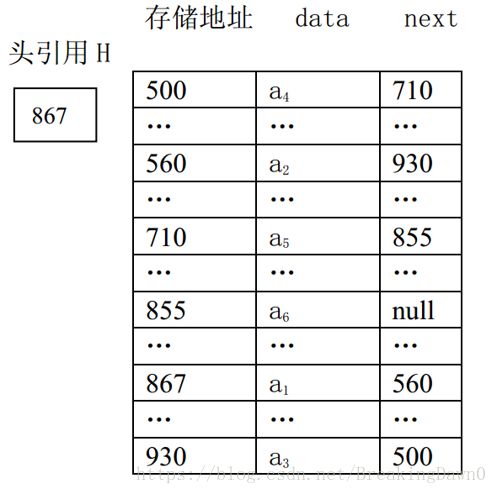
链表是用一组任意的存储单元来存储线性表中的数据元素(这组存储单元可以是连续的,也可以是不连续的)。那么,怎么表示两个数据元素逻辑上的相邻关系呢?即如何表示数据元素之间的线性关系呢?为此,在存储数据元素时,除了存储数据元素本身的信息外,还要存储与它相邻的数据元素的存储地址信息。这两部分信息组成该数据元素的存储映像(Image),称为结点(Node)。把存储据元素本身信息的域叫结点的数据域(Data Domain),把存储与它相邻的数据元素的存储地址信息的域叫结点的引用域(Reference Domain)。因此,线性表通过每个结点的引用域形成了一根“链条”,这就是“链表”名称的由来。如果结点的引用域只存储该结点直接后继结点的存储地址,则该链表叫单链表(Singly Linked List)。把该引用域叫 next。单链表结点的结构如图所示,图中 data 表示结点的数据域。
图2.3.2
下图是线性表(a1,a2,a3,a4,a5,a6)对应的链式存储结构示意图。
图2.3.3
另外一种表示形式:
图2.3.4
namespace 线性表
{
///
/// 单链表的节点类
///
///
{
private T data;//存储数据
private Node next;//指针,指向下一个节点
public Node()
{
this.data = default(T);
this.next = null;
}
public Node(T value)
{
this.data = value;
}
public Node(Node next)
{
this.next = next;
}
public Node(T value,Node next)
{
this.data = value;
this.next = next;
}
public T Data
{
get { return data; }
set { data = value; }
}
public Node Next
{
get { return next; }
set { next = value; }
}
}
}
namespace 线性表
{
///
/// 单链表实现方式
///
/// : IListDS
{
private Node headNode;//头结点
public LinkList()
{
headNode = null;
}
///
/// 按索引得到数据
///
///
/// temp = headNode;
for (int i = 1; i <= index; i++)
{
temp = temp.Next;
}
return temp.Data;
}
}
}
///
/// 添加数据
///
///
public void Add(T item)
{
Node newNode = new Node(item);//根据新的数据创建一个新的节点
if (headNode == null)//头结点为空时这个新节点即为头结点
{
headNode = newNode;
}
else//访问链表的尾节点
{
Node temp = headNode;
while (true)
{
if (temp.Next != null)
{
temp = temp.Next;
}
else
{
break;
}
}
temp.Next = newNode;//把新节点放到链表尾部
}
}
///
/// 清空链表
///
public void Clear()
{
headNode = null;
}
///
/// 删除数据
///
///
/// temp = headNode;
for (int i = 1; i <= index - 1; i++)
{
temp = temp.Next;
}
Node preNode = temp;
Node currentNode = temp.Next;
data = currentNode.Data;
Node nextNode = temp.Next.Next;
preNode.Next = nextNode;
}
return data;
}
///
/// 按索引的到数据
///
///
/// temp = headNode;
int count = 1;
while (true)
{
if (temp.Next != null)
{
count++;
temp = temp.Next;
}
else
{
break;
}
}
return count;
}
///
/// 插入数据
///
///
///
public void Insert(T item, int index)
{
Node newNode = new Node(item);
if (index == 0)//插入到头结点
{
newNode.Next = headNode;
headNode = newNode;
}
else
{
Node temp = headNode;
for(int i = 1; i <= index - 1; i++)
{
temp = temp.Next;
}
Node preNode = temp;
Node currentNode = temp.Next;
preNode.Next = newNode;
newNode.Next = currentNode;
}
}
///
/// 判断链表是否为空
///
///
/// 得到数据的索引
///
///
/// temp = headNode;
if (temp == null)
{
return -1;
}
else
{
int index = 0;
while (true)
{
if (temp.Data.Equals(value))
{
return index;
}
else
{
if (temp.Next != null)
{
temp = temp.Next;
index++;
}
else
{
break;
}
}
}
return -1;
}
}
public void ToString()
{
if (headNode == null)
{
Console.WriteLine("无数据存入");
}
else
{
Node temp = headNode;
while (true)
{
if (temp != null)
{
Console.WriteLine(temp.Data);
temp = temp.Next;
}
else
{
break;
}
}
}
}
}
}
2.3.3双向链表
前面介绍的单链表允许从一个结点直接访问它的后继结点,所以, 找直接后继结点的时间复杂度是 O(1)。但是,要找某个结点的直接前驱结点,只能从表的头引用开始遍历各结点。如果某个结点的 Next 等于该结点,那么,这个结点就是该结点的直接前驱结点。也就是说,找直接前驱结点的时间复杂度是 O(n), n是单链表的长度。当然,我们也可以在结点的引用域中保存直接前驱结点的地址而不是直接后继结点的地址。这样,找直接前驱结点的时间复杂度只有 O(1),但找直接后继结点的时间复杂度是 O(n)。如果希望找直接前驱结点和直接后继结点的时间复杂度都是 O(1),那么,需要在结点中设两个引用域,一个保存直接前驱结点的地址,叫 prev,一个直接后继结点的地址,叫 next,这样的链表就是双向链表(Doubly Linked List)。双向链表的结点结构示意图如图所示。
图2.3.5
///
/// 双向链表节点类
///
///
{
private T data; //数据域
private DbNode prev; //前驱引用域
private DbNode next; //后继引用域
//构造器
public DbNode(T val, DbNode p)
{
data = val;
next = p;
}
//构造器
public DbNode(DbNode p)
{
next = p;
}
//构造器
public DbNode(T val)
{
data = val;
next = null;
}
//构造器
public DbNode()
{
data = default(T);
next = null;
}
//数据域属性
public T Data
{
get { return data; }
set { data = value; }
}
//前驱引用域属性
public DbNode Prev
{
get { return prev; }
set { prev = value; }
}
//后继引用域属性
public DbNode Next
{
get { return next; }
set { next = value; }
}
}
2.3.4循环链表
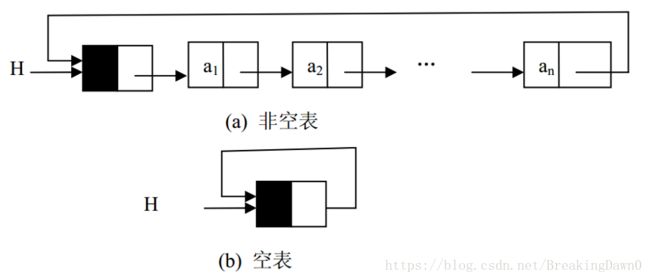
有些应用不需要链表中有明显的头尾结点。在这种情况下,可能需要方便地从最后一个结点访问到第一个结点。此时,最后一个结点的引用域不是空引用,而是保存的第一个结点的地址(如果该链表带结点,则保存的是头结点的地址),也就是头引用的值。带头结点的循环链表(Circular Linked List)如图所示。
图2.3.6
2.4栈和队列
栈和队列是非常重要的两种数据结构,在软件设计中应用很多。栈和队列也是线性结构,线性表、栈和队列这三种数据结构的数据元素以及数据元素间的逻辑关系完全相同,差别是线性表的操作不受限制,而栈和队列的操作受到限制。栈的操作只能在表的一端进行,队列的插入操作在表的一端进行而其它操作在表的另一端进行,所以,把栈和队列称为操作受限的线性表。
2.4.1栈
1.BCL中的栈
C#2.0 提供了泛型的Stack
namespace 栈
{
class Program
{
static void Main(string[] args)
{
Stack stack = new Stack();
stack.Push("Lemon");//入栈(添加数据)
stack.Push("SS");
stack.Push("13");
Console.WriteLine(stack.Peek());//取得栈顶的数据,不删除
Console.WriteLine(stack.Pop());//出栈(删除数据,返回被删除的数据)
Console.WriteLine(stack.Count);//取得栈中数据的个数
stack.Clear();//清空所有数据
Console.ReadKey();
}
}
}
2.顺序栈
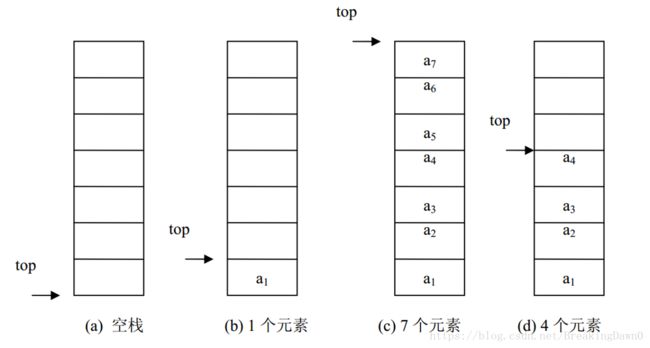
用一片连续的存储空间来存储栈中的数据元素(使用数组),这样的栈称为顺序栈(Sequence Stack)。类似于顺序表,用一维数组来存放顺序栈中的数据元素。栈顶指示器 top 设在数组下标为 0 的端, top 随着插入和删除而变化,当栈为空时,top=-1。下图是顺序栈的栈顶指示器 top 与栈中数据元素的关系图。
图2.4.1
namespace 栈
{
///
/// 栈接口
///
///
{
int Count { get; }
int GetLength();
bool IsEmpty();
void Clear();
void Push(T item);
T Pop();
T Peek();
}
}
namespace 栈
{
///
/// 顺序栈
///
/// : IStackDS
{
private T[] data;
private int top;
public SeqStack(int size)
{
data = new T[size];
top = -1;
}
public SeqStack() : this(10)
{
}
//public int Count => throw new NotImplementedException();
public int Count
{
get { return top + 1; }
}
public void Clear()
{
top = -1;
}
public int GetLength()
{
return Count;
}
public bool IsEmpty()
{
return Count == 0;
}
public T Peek()
{
return data[top];
}
public T Pop()
{
T temp = data[top];
top--;
return temp;
}
public void Push(T item)
{
data[top + 1] = item;
top++;
}
}
}
3.链栈
栈的另外一种存储方式是链式存储,这样的栈称为链栈(Linked Stack)。链栈通常用单链表来表示,它的实现是单链表的简化。所以,链栈结点的结构与单链表结点的结构一样,如图所示。由于链栈的操作只是在一端进行,为了操作方便,把栈顶设在链表的头部,并且不需要头结点。
图2.4.2
把链栈看作一个泛型类,类名为 LinkStack
namespace 栈
{
///
/// 链栈节点
///
///
{
private T data;
private Node next;
public Node()
{
data = default(T);
next = null;
}
public Node(T data)
{
this.data = data;
next = null;
}
public Node(T data,Node next)
{
this.data = data;
this.next = next;
}
public Node(Node next)
{
data = default(T);
this.next = next;
}
public T Data
{
get { return data; }
set { data = value; }
}
public Node Next
{
get { return next; }
set { next = value; }
}
}
}
namespace 栈
{
///
/// 链栈
///
/// : IStackDS
{
private Node top;//栈顶元素节点
private int count = 0;//栈中元素个数
//public int Count => throw new NotImplementedException();
public int Count
{
get { return count; }
}
public void Clear()
{
top = null;
count = 0;
}
public int GetLength()
{
return count;
}
public bool IsEmpty()
{
return count == 0;
}
public T Peek()
{
return top.Data;
}
public T Pop()
{
//出栈,取得栈顶元素并删除
T data = top.Data;
top = top.Next;
count--;
return data;
}
public void Push(T item)
{
//入栈,把新添加的元素作为栈顶元素(头)节点
Node newNode = new Node(item);
newNode.Next = top;
top = newNode;
count++;
}
}
}
2.4.2队列
队列(Queue)是插入操作限定在表的尾部而其它操作限定在表的头部进行的线性表。把进行插入操作的表尾称为队尾(Rear),把进行其它操作的头部称为队头(Front)。当队列中没有数据元素时称为空队列(Empty Queue)。
队列通常记为: Q= (a1,a2,…,an),Q是英文单词queue的第 1 个字母。a1为队头元素,an为队尾元素。这n个元素是按照a1,a2,…,an的次序依次入队的,出对的次序与入队相同,a1第一个出队,an最后一个出队。所以,对列的操作是按照先进先出(First In First Out)或后进后出( Last In Last Out)的原则进行的,因此,队列又称为FIFO表或LILO表。队列Q的操作示意图如图所示。
图2.4.3
在实际生活中有许多类似于队列的例子。比如,排队取钱,先来的先取,后来的排在队尾。
队列的操作是线性表操作的一个子集。队列的操作主要包括在队尾插入元素、在队头删除元素、取队头元素和判断队列是否为空等。与栈一样,队列的运算是定义在逻辑结构层次上的,而运算的具体实现是建立在物理存储结构层次上的。因此,把队列的操作作为逻辑结构的一部分,每个操作的具体实现只有在确定了队列的存储结构之后才能完成。队列的基本运算不
是它的全部运算,而是一些常用的基本运算。
1.BCL中的队列
C#2.0 提供了泛型Queue
namespace 队列
{
class Program
{
static void Main(string[] args)
{
Queue queue = new Queue();
//入队
queue.Enqueue(1);//队首
queue.Enqueue(2);
queue.Enqueue(3);//队尾
Console.WriteLine(queue.Peek());//取得队首的元素,不移除
Console.WriteLine(queue.Dequeue());//出队,移除队首元素,并返回被移除的元素
Console.WriteLine(queue.Count);//获取队列中元素的个数
queue.Clear();//清空元素
Console.ReadKey();
}
}
}
2.(循环)顺序队列
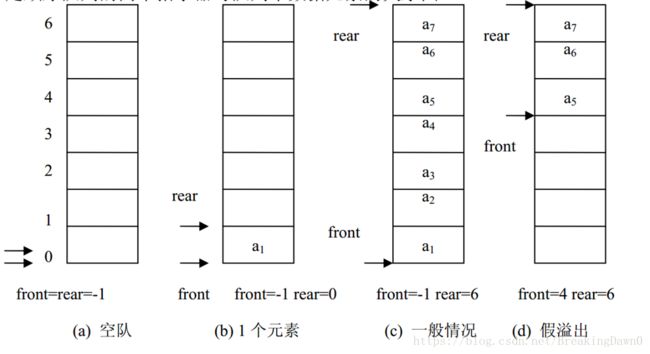
用一片连续的存储空间来存储队列中的数据元素,这样的队列称为顺序队列(Sequence Queue)。类似于顺序栈,用一维数组来存放顺序队列中的数据元素。队头位置设在数组下标为 0 的端,用 front 表示;队尾位置设在数组的另一端,用 rear 表示。 front 和 rear 随着插入和删除而变化。当队列为空时, front=rear=-1。图是顺序队列的两个指示器与队列中数据元素的关系图。
图2.4.4
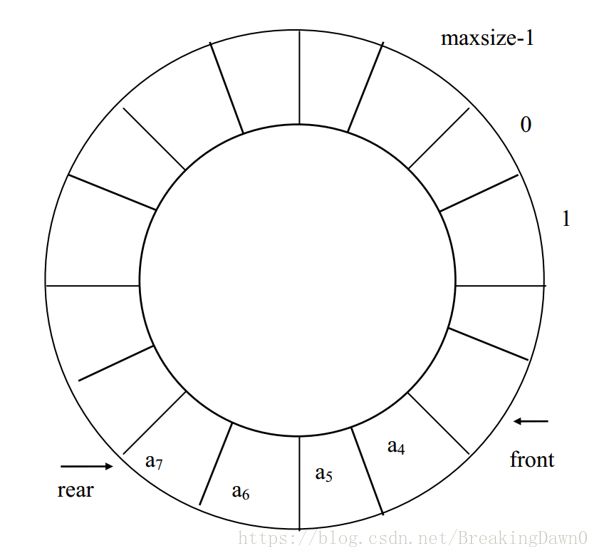
如果再有一个数据元素入队就会出现溢出。但事实上队列中并未满,还有空闲空间,把这种现象称为“假溢出”。这是由于队列“队尾入队头出”的操作原则造成的。解决假溢出的方法是将顺序队列看成是首尾相接的循环结构,头尾指示器的关系不变,这种队列叫循环顺序队列(Circular sequence Queue)。循环队列如图所示。
图2.4.5
namespace 队列
{
///
/// 队列接口
///
///
{
int Count { get; }//取得队列长度的属性
int GetLength(); //求队列的长度
bool IsEmpty(); //判断对列是否为空
void Clear(); //清空队列
void Enqueue(T item); //入队
T Dequeue(); //出队
T Peek(); //取队头元素
}
}
namespace 队列
{
///
/// 循环顺序队列
///
/// : IQueueDS
{
private T[] data;
private int count;//当前元素个数
private int front;//队首(队首元素索引-1)
private int rear;//队尾(队尾元素索引)
public SeqQueue(int size)
{
data = new T[size];
count = 0;
front = -1;
rear = -1;
}
public SeqQueue() : this(10) { }
public int Count
{
get { return count; }
}
public void Clear()
{
count = 0;
front = rear = -1;
}
public T Dequeue()
{
if (count > 0)
{
T temp = data[front + 1];
if (front < data.Length - 1)
{
front++;
}
else
{
front = -1;
}
count--;
return temp;
}
else
{
Console.WriteLine("队列为空");
return default(T);
}
}
public void Enqueue(T item)
{
if(count == data.Length)
{
Console.WriteLine("队列已满");
}
else
{
if (rear == data.Length - 1)
{
data[0] = item;
rear = 0;
count++;
}
else
{
data[rear + 1] = item;
rear++;
count++;
}
}
}
public int GetLength()
{
return Count;
}
public bool IsEmpty()
{
return count == 0;
}
public T Peek()
{
T temp = data[front + 1];
return temp;
}
}
}
3.链队列
队列的另外一种存储方式是链式存储,这样的队列称为链队列(Linked Queue)。同链栈一样,链队列通常用单链表来表示,它的实现是单链表的简化。所以,链队列的结点的结构与单链表一样,如图所示。由于链队列的操作只是在一端进行,为了操作方便,把队头设在链表的头部,并且不需要头结点。
图2.4.6
namespace 队列
{
///
/// 链队列节点
///
///
{
private T data; //数据域
private Node next; //引用域
//构造器
public Node(T val, Node p)
{
data = val;
next = p;
}
//构造器
public Node(Node p)
{
next = p;
}
//构造器
public Node(T val)
{
data = val;
next = null;
}
//构造器
public Node()
{
data = default(T);
next = null;
}
//数据域属性
public T Data
{
get
{
return data;
}
set
{
data = value;
}
}
//引用域属性
public Node Next
{
get
{
return next;
}
set
{
next = value;
}
}
}
}
namespace 队列
{
///
/// 链队列
///
/// : IQueueDS
{
private Node front;
private Node rear;
private int count;
public LinkQueue()
{
front = null;
rear = null;
count = 0;
}
public int Count
{
get { return count; }
}
public void Clear()
{
front = null;
rear = null;
count = 0;
}
public T Dequeue()
{
if(count == 0)
{
Console.WriteLine("队列为空");
return default(T);
}
else if(count == 1)
{
T temp = front.Data;
front = rear = null;
count = 0;
return temp;
}
else
{
T temp = front.Data;
front = front.Next;
count--;
return temp;
}
}
public void Enqueue(T item)
{
Node newNode = new Node(item);
if(count == 0)
{
front = newNode;
rear = newNode;
count++;
}
else
{
rear.Next = newNode;
rear = newNode;
count++;
}
}
public int GetLength()
{
return Count;
}
public bool IsEmpty()
{
throw new NotImplementedException();
}
public T Peek()
{
if (front != null)
{
return front.Data;
}
else
{
return default(T);
}
}
}
}
2.4.3栈和队列应用实例
编程判断一个字符串是否是回文。回文是指一个字符序列以中间字符为基准两边字符完全相同,如字符序列“ ACBDEDBCA”是回文。
算法思想:判断一个字符序列是否是回文,就是把第一个字符与最后一个字符相比较,第二个字符与倒数第二个字符比较,依次类推,第 i 个字符与第 n-i个字符比较。如果每次比较都相等,则为回文,如果某次比较不相等,就不是回文。因此,可以把字符序列分别入队列和栈,然后逐个出队列和出栈并比较出队列的字符和出栈的字符是否相等,若全部相等则该字符序列就是回文,否则就不是回文。
namespace 栈和队列应用
{
class Program
{
static void Main(string[] args)
{
Stack stack = new Stack();
Queue queue = new Queue();
string str = Console.ReadLine();
bool isHuiWen = true;
for(int i = 0; i < str.Length; i++)
{
stack.Push(str[i]);
queue.Enqueue(str[i]);
}
while (stack.Count > 0)
{
if (stack.Pop() != queue.Dequeue())
{
isHuiWen = false;
break;
}
}
Console.WriteLine(isHuiWen);
Console.ReadKey();
}
}
}
2.5串和数组
2.5.1串
1.串的概念
在应用程序中使用最频繁的类型是字符串。字符串简称串,是一种特殊的线性表,其特殊性在于串中的数据元素是一个个的字符。字符串在计算机的许多方面应用很广。如在汇编和高级语言的编译程序中,源程序和目标程序都是字符串数据。在事务处理程序中,顾客的信息如姓名、地址等及货物的名称、产地和规格等,都被作为字符串来处理。另外,字符串还具有自身的一些特性。因此,把字符串作为一种数据结构来研究。
串(String)由 n(n≥0)字符组成的有限序列。一般记为:
S=”c1c2…cn” (n≥0)
其中, S是串名,双引号作为串的定界符,用双引号引起来的字符序列是串值。 ci( 1≤i≤n)可以是字母、数字或其它字符, n为串的长度,当n=0 时,称为空串(Empty String)。
串中任意个连续的字符组成的子序列称为该串的子串(Substring)。包含子串的串相应地称为主串。子串的第一个字符在主串中的位置叫子串的位置。如串s1”abcdefg”,它的长度是 7,串s2”cdef”的长度是 4, s2是s1的子串, s2的位置是 3。
如果两个串的长度相等并且对应位置的字符都相等,则称这两个串相等。而在 C#中,比较两个串是否相等还要看串的语言文化等信息。
2.c#中的串
在 C#中,一个 String 表示一个恒定不变的字符序列集合。 String 类型是封闭类型,所以,它不能被其它类继承,而它直接继承自 object。因此, String 是引用类型,不是值类型,在托管堆上而不是在线程的堆栈上分配空间。String类型还继承了 IComparable 、 ICloneable 、 IConvertible 、 IComparable
在 C#中,创建串不能用 new 操作符,而是使用一种称为字符串驻留的机制。这是因为 C#语言将 String 看作是基元类型。基元类型是被编译器直接支持的类型,可以在源代码中用文本常量(Literal)来直接表达字符串。当 C#编译器对源代码进行编译时,将文本常量字符串存放在托管模块的元数据中。而当 CLR 初始化时, CLR 创建一个空的散列表,其中的键是字符串,值为指向托管堆中字符串对象的引用。散列表就是哈希表。当 JIT编译器编译方法时,它会在散列表中查找每一个文本常量字符串。如果找不到,就会在托管堆中构造一个新的 String 对象(指向字符串),然后将该字符串和指向该字符串对象的引用添加到散列表中;如果找到了,不会执行任何操作。
3.定义一个串
由于串中的字符都是连续存储的,而在 C#中串具有恒定不变的特性,即字符串一经创建,就不能将其变长、变短或者改变其中任何的字符。所以,这里不讨论串的链式存储,也不用接口来表示串的操作。同样,把串看作是一个类,类名为 StringDS。取名为 StringDS 是为了和 C#自身的字符串类 String 相区别。类StringDS 只有一个字段,即存放串中字符序列的数组 data。由于串的运算有很多,类 StringDS 中只包含部分基本的运算。
namespace 串
{
///
/// 串的实现
///
class StringDS
{
private char[] data;
//构造器
public StringDS(char[] array)
{
data = new char[array.Length];
for(int i = 0; i < data.Length; i++)
{
data[i] = array[i];
}
}
public StringDS(string str)
{
data = new char[str.Length];
for (int i = 0; i < data.Length; i++)
{
data[i] = str[i];
}
}
public StringDS() { data = null; }
//根据索引取字符的索引器
public char this[int index]
{
get { return data[index]; }
}
//获取字符串长度
public int GetLength()
{
return data.Length;
}
///
/// 当前字符串等于s,返回0
/// 当前字符串小于s,返回-1
/// 当前字符串大于s,返回1
///
///
///
/// 查询串
/// 返回当前串中首个与s相同的子串的首索引
///
///
/// 2.5.2数组
数组是一种常用的数据结构,可以看作是线性表的推广。数组作为一种数据结构,其特点是结构中的数据元素可以是具有某种结构的数据,甚至可以是数组,但属于同一数据类型。数组在许多高级语言里面都被作为固定类型来使用。
数组是 n(n≥1)个相同数据类型的数据元素的有限序列。一维数组可以看作是一个线性表,二维数组可以看作是“数据元素是一维数组”的一维数组,三维数组可以看作是“数据元素是二维数组”的一维数组,依次类推。
C#支持一维数组、多维数组及交错数组(数组的数组)。所有的数组类型都隐含继承自System Array。Array 是一个抽象类,本身又继承自 System.Object。所以,数组总是在托管堆上分配空间,是引用类型。任何数组变量包含的是一个指向数组的引用,而非数组本身。当数组中的元素的值类型时,该类型所需的内存空间也作为数组的一部分而分配;当数组的元素是引用类型时,数组包含是只是引用。
using System;
using System.Collections;
public abstract class Array : ICloneable, IList, ICollection, IEnumerable
{
//判断 Array 是否具有固定大小。
public bool IsFixedSize { get; }
//获取 Array 元素的个数。
public int Length { get; }
//获取 Array 的秩(维数)。
public int Rank { get; }
//实现的 IComparable 接口,在.Array 中搜索特定元素。
public static int BinarySearch(Array array, object value);
//实现的 IComparable
public static int BinarySearch
//实现 IComparable 接口,在 Array 的某个范围中搜索值。
public static int BinarySearch(Array array, int index,
int length, object value);
//实现的 IComparable
public static int BinarySearch
int index, int length, T value);
//Array 设置为零、 false 或 null,具体取决于元素类型。
public static void Clear(Array array, int index, int length);
//System.Array 的浅表副本。
public object Clone();
//从第一个元素开始复制 Array 中的一系列元素
//到另一 Array 中(从第一个元素开始)。
public static void Copy(Array sourceArray,
Array destinationArray, int length);
//将一维 Array 的所有元素复制到指定的一维 Array 中。
public void CopyTo(Array array, int index);
//创建使用从零开始的索引、具有指定 Type 和维长的多维 Array。
public static Array CreateInstance(Type elementType,
params int[] lengths);
//返回 ArrayIEnumerator。
public IEnumerator GetEnumerator();
//获取 Array 指定维中的元素数。
public int GetLength(int dimension);
//获取一维 Array 中指定位置的值。
public object GetValue(int index);
//返回整个一维 Array 中第一个匹配项的索引。
public static int IndexOf(Array array, object value);
//返回整个.Array 中第一个匹配项的索引。
public static int IndexOf
//返回整个一维 Array 中最后一个匹配项的索引。
public static int LastIndexOf(Array array, object value);
//反转整个一维 Array 中元素的顺序。
public static void Reverse(Array array);
//设置给一维 Array 中指定位置的元素。
public void SetValue(object value, int index);
//对整个一维 Array 中的元素进行排序。
public static void Sort(Array array);
}
C#数据结构与算法基础之一:基本概念 上一章 下一章