汉诺塔思路整理---Python
汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。
大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
①大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
②并且规定,在小圆盘上不能放大圆盘
③在三根柱子之间一次只能移动一个圆盘
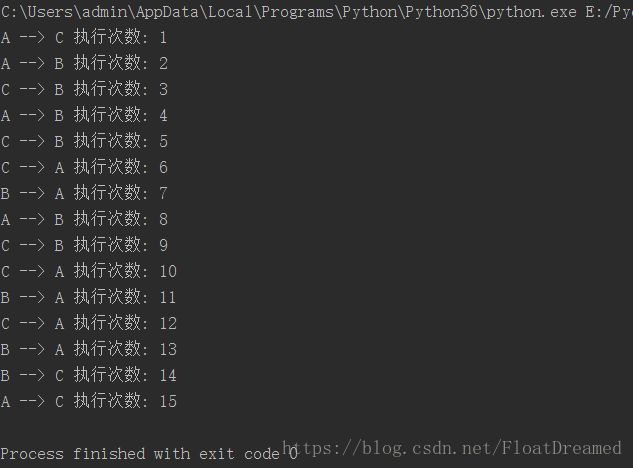
试问:假设有4个盘子的话,请计算共需移动的次数并将操作的步骤列出
这里是递归函数的应用,假设这里有ABC三根柱子,下面来分析一下思路
(关于解法网上的答案很多,但是很难让人明白递归究竟是怎么运用进去的)
①A柱上有1个盘子,需要移动S1=1次就可以将盘子全部移动到另一根柱子上
②A柱上有2个盘子,需要移动S2=3次就可以将盘子全部移动到另一根柱子上
③A柱上有3个盘子,按照大小从上到下分别标记为p1、p2、p3
1>由②可以知道将A柱上的p1和p2移动到C柱上花费次数3次
2>将A柱上的p3移动到B柱上花费次数为1次
3>由②可以知道再将此时C柱上的p1和p2移动到B柱上花费次数仍为3次
所以总结出A柱上有3个盘子,需要移动S3=2*3+1=7次就可以将盘子全部移动到另一根柱子上
记住这里是在借助②的原理的基础上算出来的
④A柱上有4个盘子时,按照大小从上到下分别标记为p1、p2、p3、p4
1>由③可以知道将A柱上的p1、p2和p3移动到C柱上花费次数7次
2>将A柱上的p4移动到B柱上花费次数为1次
3>由③可以知道再将此时C柱上的p1、p2和p3移动到B柱上花费次数仍为7次
所以总结出A柱上有4个盘子,需要移动S4=2*7+1=15次就可以将盘子全部移动到另一根柱子上
记住这里是在借助③的原理的基础上算出来的
⑤A柱上有N个盘子时,按照大小从上到下分别标记为p1、p2、p3、p4.......pN
1>将A柱上的p1、p2、p3、p4.......pN-1移动到C柱上花费次数S(N-1)次
*******至于这里的S(N-1)是A柱上有N-1个盘子时,将盘子全部移动到另一根柱子上所花费的次数
2>将A柱上的pN移动到B柱上花费次数为1次
3>再将此时C柱上的p1、p2、p3、p4.......pN-1移动到B柱上花费次数仍为S(N-1)次
所以总结出A柱上有4个盘子,需要移动SN=2*S(N-1)+1=15次就可以将盘子全部移动到另一根柱子上
上面总结出一个关于计算次数的递归公式,下面来思考一下使用python模拟移动操作的思路:
①将A柱上面的N-1个盘子移动至C柱(此时A柱上只剩下了一个最大的盘子)
move(n-1, a, b, c)②将A柱上剩下的这1个最大的盘子移动至B柱(此时A柱空了,B柱上有一个最大的盘子,C柱上有其余的盘子)
move(1, a, c, b)③将C柱上那N-1个盘子移动至B柱的大盘子上(完工)
move(n-1, c, a, b)上代码了:
# _*_ coding:utf-8 _*_
__author__ = 'admin'
'''
汉诺塔
汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。
大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘
'''
# 统计执行次数
count = 0
def move(n, a, b, c):
global count
if n == 1:
count += 1
print(a, "-->", c, "执行次数:", count)
else:
# 首先需要把 (N-1) 个圆盘移动到 c
move(n-1, a, b, c)
# 将a的最后一个圆盘移动到b
move(1, a, c, b)
# 再将c的(N-1)个圆盘移动到a
move(n-1, c, a, b)
move(4, "A", "B", "C")执行结果如下: