数论入门
数论入门
虽然大一学c语言的时候就学了辗转相除法也(欧几里得算法),但是当时没学透,没有搞清楚为啥子这样辗转相处就能得到最大公约数,这来一段书上的话
确实这么一段话就搞清楚为啥要辗转相除了,然后就是扩展欧几里得算法,而扩展欧几里得算法就是用来解决线性同余方程的ax ≡ c (mod b),夜深人静写算法(初等数论) , 这篇文章讲得很细, 文中的推导就是d = gcd(a, b) = gcd(b, a%b) = bx' + (a%b)y' = bx' + [a-b*(a/b)]y' = ay' + b[x' - (a/b)y']
模板代码:
int ex_gcd(int a, int b, int &x, int &y){
if(b == 0){
x = 1; y = 0;
return a;
}else{
int answer = ex_gcd(b, a%b, x, y);
int temp = x;
x = y;
y = temp - a/b * y;
return answer;
}
}
我也想了一哈非递归的代码,但是确实目前水平不够,想不出来,因为这个不像辗转相除法可以递推,这个必须先递归到底,然后再回来的时候才能根据求得的x,y递推
poj1061 poj2115
poj1061这是扩展欧几里得算法的入门题,poj2115也是类似, 也可以归为线性同余方程,就是两只青蛙一只切追另外一只,当让肯定要速度快的去追速度慢的。我第一反应就是用小学学的追击问题切解决,但是有问题,因为他们走的路是一个环也就是说虽然使用路程差 / 速度差 = 所需次数 但是,这里的速度有可能是大于路程差的而且青蛙是一次一次的跳也就是整数,不能结果来小数,也就是速度快的那只青蛙有可能直接一跳直接就跳到了速度慢的那只青蛙的前头,然后他们就有可能绕地球及几圈以后才会相遇,这么以来就不能直接除了,但是也不能就用暴力慢慢搞跳几次才相遇三,所以就用到了传说中线性同余方程速度差 * x ≡ 路程差(mod 总路程),然后就用扩展欧几里得算法套就行了,但是求出来的是这是其中一个解,而题目中要求最小非负解,这就需要对同余方程解一个深刻理解才能很自然的用通解得到
博客推荐
青蛙约会详解
青蛙题解
这是我从文中截图,这里讲得很到位,一看就懂,一哈就领会了啥子通解,在那个范围由唯一解这些东西, 然后这道题也就出来了

还有一个小问题就是c++的负数取模
int a = -3;
cout << a % 2 << endl;
结果是 -1
poj2142
这道题跟上面的也差不多,也要先用扩展欧几里得算法处理,然后对于解体重要求在所有的解中,取砝码数量最小的组合, 如果砝码组合相同,就取用的砝码总重量最小的组合,这道题的难点也就在这,求两种砝码数量总和最小的那组。
我是通过画图来解决,因为上面所讲的,通解可以表示为
x = (x0 + kb/gcd)
y = (y0 - ka/gcd)
当然后这里的x ,y有可能一正一负, 也有可能都为正,所以要求 x + y 的最小值 也就是要求 |x| + |y|, 这里就用到了高中学的东西,图中为这两个绝对值的图像,因为加了绝对值,x下面的部分都翻了上来,然后x和y和x轴一定各自相较于一点,然后这两个v字型随便一定就行了,不管怎么移动,他们必有交点,也就是图中的a点,从这的点往右走,|x| + |y|的值会增加因为,增加了b但是只减少了c,其他区域都是都是同理,所以那个最小值的点就是看哪个函数斜率大,然后就找斜率大的那个函数与x轴的交点,然后这个交点左右最相临的整数点,判断这两个点是某相等,然后找最小的那个点,然后就简单了
#include费马小定理
假如a是整数,p是质数,则a,p显然互质(即两者只有一个公约数1),
就有:a^(p-1) ≡ 1 (mod p)
这篇文章是证明过程 :费马小定理
通过这篇文章,根据3*6*9*12*15*18*21*24*27*30*33*36 ≡ 3*6*9*12*2*5*8*11*1*4*7*10 mod 13 (因为3和13互质,所以1,2,.. 12 乘上3后还是和13互质,12个数还是和1到12同余 ,只是顺序不同了 )。 所以312×12!≡12!mod 13。
其实费马小定理成立的根本原因就在于构成了312×12!≡12!mod 13,然后两边同时除以那个阶乘就得到了费马小定理,我的第一感觉就是公式中的p不一定非要是素数公式才成立(已被证明有伪素数存在,所以确实不一定是素数才成立),因为之所以能够成3*6*9*12*15*18*21*24*27*30*33*36 ≡ 3*6*9*12*2*5*8*11*1*4*7*10 mod 13 这种同余式,是因为a与p互素,而a与p互素的时候p不一定是素数比如3和9,然后a乘以1 2 3 。。。。 n-1, 的时候之所以能一一对应就是因为这个a在乘的时候因为与p互素,就会错开,草稿纸上写一哈就有感觉了。。所以像这种312×12!≡12!mod 13式子很容易得到,比如256 x 8!≡ 8! (mod 9) 但是并不能得到2^8 ≡ 1 (mod 9),这里的问题就是同余式除法,这是从百度上截的图
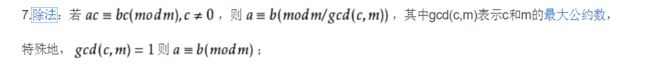
但是伪素数又该怎么解释喃,如下图
实验是检验整理的唯一标准,所以确实费马小定理前提是必要不充分的,那为什么会有这个问题?这里就要解决上面的同余式除法的本质。这是我从网上看到一个证明
因为 m|ac-bc
所以 m/(c,m)|c/(c,m)*(a-b)
而(m/(c,m),c/(c,m))=1
所以m/(c,m)|a-b
也就是说:a ≡ b (mod m/(c,m))
从这个证明看出a≡ b (mod m/(c,m)) 其实本质是这个式子m/(c,m)|c/(c,m)*(a-b),只不过其中而m/(c,m)和c/(c,m)是互素的,所以能判断(a-b)是被m/(c, m)除尽,而不是c/(c,m)被除尽,但是这并不能说明(a-b)是被m/(c, m)除尽的时候,c/(c,m)非要和m/(c, m)互素,也就是说他们有可能都被除尽的时候,而341这个伪素数就是这种情况,所以上面同余式除法成立的条件的是必要不充分的所以就导致a^(p-1) x (p-1)! ≡ (p-1)! (mod p) 的时候要求(p-1) 和 p 互素,也就是为什么费马说p一定要是素数的原因,因为如果p是素数,他们就一定互素。
取模和位运算的速度差异
#include效果:
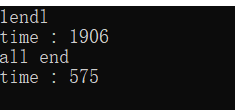
其实不管是取模和&运算有这种差距,包括除法(/) 和 左移运算 (>>) 也有这种差距
判断素数的题
poj2262水题,直接试除法
poj3641大整数判素,需要下面的算法
poj1811需要下面两个算法,模板提
poj2429首先要理解最大公约数和最大公倍数的关系,然后就是要枚举所有组合,我最早感觉枚举不炫,就自作聪明的想了一些办法都是错的
拉宾米勒算法(Rabin-Miller)
拉宾米勒算法就是用来判断素数的,只不过如果需要判断的素数不是很大用这个算法反而适得其反,比如筛选就相当巴适,但是需要判断的这个数是一个很大的数,比如有18位(long long),如果还用筛选就有点恼火了,因为不得不找一个18位这么长的数组,而且还要从2一直循环到1e18,不超时和不超内存都是不可能的,所以这个时候就是拉宾米勒算法的表演时间了。
这篇文章讲了一下费马小定理,以及由费马小定理而应出的伪素数和欧拉定理的一些小问题他么的因果关系,以及最后引出的拉宾米勒算法Miller-Rabin算法素数与素数测试, 这篇文章中的防止溢出技巧,我开始都没当回事,直到后来。。。
总结一哈,最早因为有费马小定理,所以可以直接用a^(p-1) % p = 1来判断是否p是素数,但是这个有点问题就是因为费马小定理的必要不充分性,也就是存在一些合数使得这个公式成立,所以我们就多找几个a来判断,这样就能降低因为伪素数也能让费马小定理成立的而出现的问题,这就是费马测试。
但是除了伪素数之外还有一种数更凶,他能通过所有比他小的a的的费马测试,也就是卡迈克尔数Carmichael
虽然说概率不是很高但是还是不能接受,所以在费马测试的基础上又出现了Rabin-Miller素数测试,它的核心就是再使用费马测试基础之上,根据一个基本公式,这里就用上面那篇文章的内容
溜就溜在这个公式(x+1)(x-1) % p = 0,因为x是小于p的(因为所有的x都是模p后的结果),如果p是素数,模p等于0的的数只有0和p本身,如果是合数,就会可能出现其他的情况
Rabin-MIller算法模板
ll shuzu[9] = {2,3,5,7,11,13,17,19,23};
//ll shuzu[10] = {2, 3, 5, 7,11,31,61,73,233,331};
ll mul(ll a, ll b, ll n){
ll answer = 0;
a %= n;
while(b){
if(b & 1) answer = (answer + a) % n;
a = (a + a) % n;
b >>= 1;
}
return answer;
}
ll poww(ll a, ll b, ll n){
ll answer = 1;
a %= n;
while(b){
if(b & 1) answer = mul(answer, a, n) % n;
a = mul(a, a, n) % n;
b >>= 1;
}
return answer;
}
bool feima(ll a, ll n, ll k, ll m){
ll pre = poww(a, m, n) % n;
if(pre == 1)
return false;
while(k --){
ll next = mul(pre, pre, n) % n;
if(next==1 && pre!=1 && pre!=n-1)
return true;
pre = next;
}
return (pre != 1);
}
bool isprime(ll n){
ll k = 0, m = n - 1;
if(n == 2) return true;
if(n<2 || !(n&1)) return false;
while( !(m&1)) {k++; m >>= 1;} //先把大数化简到最小,后面二次探测从小往大判断,防止溢出
for(int i = 0; i < 9; i++){
if(n == shuzu[i])
return true;
if(feima(shuzu[i], n, k, m))
return false;
}
return true;
}
这其中用了两重快速幂,下面有讲解
当我在研究Pollard Rho查询大整数因子算法的时候,我想测试一哈一个大素数,和一个大合数在使用Pollard Rho的速度差异(那种17、18位长的数),然后我自己随便写了几个循环用Rabin-Miller判断是不是素数,结果找了很久都没有找到,众里寻他千百度。。。最后我在网上找大一篇文章,关于解决快速判断longlong型的整数是否为素数, 他说有一个18位素数154590409516822759,然后我就用我刚学的Rabin-Miller测一了哈,结果不对!!!
然后经过我一番调试,终于找到了问题的根源,那就是数据溢出问题,也就是在使用快速幂惩罚的时候出现的因为取模的数太大比如 1e17 % 1e18 = 1e17,但是如果1e17 * 1e17 % 1e18的时候就会出现查过了long long的最大数据长度,解决这个问题的办法很溜,只用把乘法替换成加法,这是你可能会说加法虽然可以没加一次的时候取模,但是像1e17 * 1e17循环下来还是很慢,根本不行啊。普通循环加法不行就用快速幂加法,轻轻松松就解决了。。
解决快速幂乘法的办法模板:
ll mul(ll a, ll b, ll n){
ll answer = 0;
a %= n;
while(b){
if(b & 1) answer = answer + a % n;
a = a + a % n;
b >>= 1;
}
}
ll poww(ll a, ll b, ll n){
ll answer = 1;
a %= n;
while(b){
if(b & 1) answer = mul(answer, a, n) % n;
a = mul(a, a, n);
b >>= 1;
}
return answer;
}
以后用快速幂的时候最后都这样组合用, 比较稳妥,免得数据溢出。
Pollard Rho分解因子算法
波拉德算法–Pollard Rho,是用来查找一个大整数中的因子,我刚刚学习这个算法的时候,我看到居然是用随机数来判断是否能整除的时候(相当于是在猜),感觉很懵。。哪见到过用随机出来猜因子的啊,那效率岂不是比用循环一个一个挨到搞还慢,然后就跟在研究玄学一样。。。下面的文章很推荐,建议配合研究
大数质因解:浅谈Miller-Rabin和Pollard-Rho算法
Rollard Rho文章翻译
还是随机数的问题,为什么要随机数喃?随机数给我的第一感觉还不如用循环,因为随机数又是伪随机而且还有可能重复,所以效率肯定低三~。但是,这里的重复就有点意思了,有个东西叫做生日悖论,来一张百度百科的图解
神不神奇,意不意外,玄学不玄学,但是不管他吹的有好神,时间是检验真理的唯一标准,一切从实际出发,理论结合实际,实事求是,在实践中检验真理并发展真理,写个程序验证一哈
#include虽然说了这么的多的生日悖论,但是我之前感觉在Pollard-Rho算法中其实也就只是提升了一点几率,因为大多数模板(包括维基百科给的代码),都只是每次生成俩个随机数,然后用这两个随机数做差取绝对值,后来我在看别人的文章中都会说是从1, 2, 。。。n-1这些数中取,因为我们是取模,其实就相当于我们已经有了很多人(然后我们只是负责从汇总随便抽取两个人来判断)。而且在实际中,我们一般都不用随机函数,一般用自己定义的一个生成函数f(x) = x^2 + c(c是自己定义的一个常数),而在不停修改c的过程中,基本上可以遍历到所有比n小的数。
但是现在的概率还不够,还能增加猜中的概率,就是通过gcd,随便找两个比n小的数,他们差得绝对值刚好能被n整除的概率,还是不大,但是如果他们差的绝对值和n有相同的因子,也就是他们的差是n因子的倍数几率就又提升了
还有个问题就是判圈,之前用kruskal的时候,判断环用的是并查集,但是这里好像有点区别,这里是循环节。。。比如说一个函数F(x) = (F(x-1)^2 + 1) % 44,而F(0) = 1的时候,就会出现一个数列2, 5, 26, 17, 26, 17, 26, 17, 。。。,可以看出,这个数列先经过两个数,然后就进入了一个圈中,这里借用 Pollard-Rho算法详解 这篇文章中的图
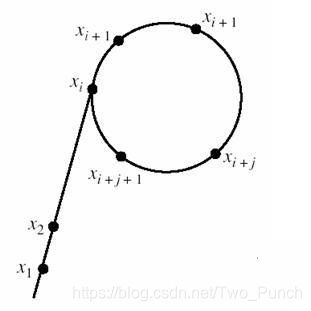
也就和希腊字母中的很像,下图中最右边那个字母,不过确实没想到这个算法的名字这么有内涵~

这里的圈是一定会出现的,因为随便一个数n,只要n已确定,那么小于n的正整数就是有限的,在取模的时候,只要在某次运算后,与之前的某个数相同,就进入了圈。
Pollard-Rho算法判圈
所以现在最后一个问题就是要解决这个圈的问题,也就是怎么让唐僧走出这个圈,我现在了解到有两种判圈,一种是floyd,一种是brent,感觉floyd的讲解信息最多,但是我在网上搜Pollard-Rho算法模板,大家基本上都用的是brent,而且我感觉用floyd有一个问题,那就是当判断数是4的时候,虽然判圈是对的,但是没法让a和b的差刚好等于2(4除了1和本身之外只有2这个唯一的因子)也就是要让a和b分别等于0、2或者1、3,但是弗洛伊德判圈是让b推导的速度是a的两倍,也就是说他们两个会错过很多组合。。。我也没搞醒活,我只是在运行的时候遇到这个问题。而且网上很多的模板基本上都没有用弗洛伊德,用的是brent,这个确实也玄学,反正感觉不是很清楚,目前也就维基百科上面我看到的讲解最多Brent’s algorithm
Pollar-Rho算法模板:
ll absabs(ll input){
if(input < 0) input *= -1;
return input;
}
ll gcd(ll a, ll b){
ll c = a % b;
while(c){
a = b;
b = c;
c = a % b;
}
return b;
}
ll find_factor(ll n, ll c){
ll a = 2, b = a, i = 0, k = 1;
while(1){
i ++;
a = (mul(a, a, n) + c ) % n;
ll p = gcd(absabs(a-b), n);
if(p!=1 && p!=n) return p;
if(a == b) return -1;
if(i == k){
b = a;
k <<= 1;
}
}
}
void find(ll n, ll c){
if(n==1 || isprime(n)){
shuzu[length++] = n;
return ;
}
ll temp = -1;
ll cc = c;
while(temp == -1) temp = find_factor(n, cc--);
find(temp, c);
find(n / temp, c);
}
这个大整数123456789123456798用来测试Pollard-Rho算法还可以
筛选素数
最出名的,埃氏筛,模板
void init(){
memset(shuzu, 0, sizeof(shuzu));
for(int i = 2; i < maxn; i++){
if(!shuzu[i]) shuzu[++shuzu[0]] = i;
for(int j = 1; j<=shuzu[0] && i*shuzu[j]<maxn; j++){
shuzu[i*shuzu[j]] = 1;
}
}
// for(int i = 0; i < 100; i ++) cout << shuzu[i] << " "; cout << endl;
}
poj3978直接用埃氏筛
有些时候求一个区间的素数,并不会从0开始,或者很大的时候,会用到容斥原理,我这里就只记录埃氏筛法,直接上书上的讲解
poj2689
就是照着上图的讲解
#include