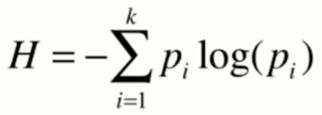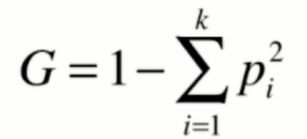机器学习基础-10.决策树
一、决策树
1.概念
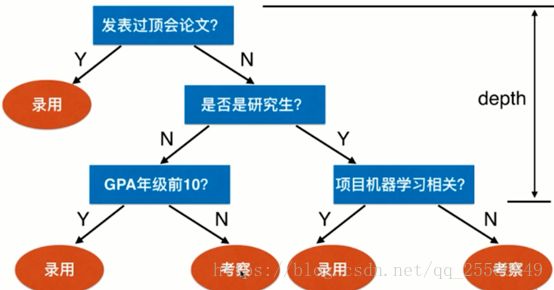
决策树在现实生活中应用广泛,也非常容易理解,通过构建一颗决策树,只要根据树的的判断条件不断地进行下去,最终就会返回一个结果。例如下图所示。决策树天然地可以解决多分类问题,同时也可以应用于回归问题中。
现在先通过sklearn中封装的决策树方法对数据进行分类,来学习决策树。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
x=iris.data[:,2:]#这里就用了2个特征
y=iris.target
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.scatter(x[y==2,0],x[y==2,1])
plt.show()from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(max_depth=2,criterion="entropy") #决策树深度2
dt.fit(x,y)
def plot_decision_boundary(model,axis):
x0,x1 = np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1)
)
x_new = np.c_[x0.ravel(),x1.ravel()]
y_predict = model.predict(x_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0,x1,zz,linewidth =5,cmap=custom_cmap)
plot_decision_boundary(dt,axis=[0.5,7.5,0,3])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.scatter(x[y==2,0],x[y==2,1])
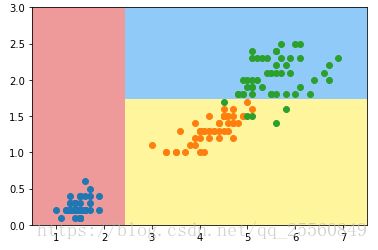
plt.show()得出来的决策边界可以绘制出如下右图所示的决策树,当数据小于2.4时就分为A,如果大于2.4就继续考察,当这部分的样本y小于1.8时就分为B,如果大于1.8就分为C。这个决策树总共的深度为2,即有2层判断条件。但是这个决策依据是如何得出来的?又该在哪个维度哪个值进行划分?下面介绍一个重要的概念-信息熵。
2.信息熵
熵在信息论中代表随机变量不确定度的度量,由香农提出来的。熵越大,数据的不确定性越高,数据越混乱;熵越小,数据的不确定性越低,数据越趋向于集中统一。计算公式如下,k代表类别,pi代表这个类别所对应的概率是多少。
对于一个数据集,假设其各个类别所对应的比重都为1/3,则H=-1/3log(1/3)-1/3log(1/3)-1/3log(1/3)=1.0986。
对于一个数据集,假设其各个类别所对应的比重分别为{1/10,2/10,7/10},则H=-1/10log(1/10)- 2/10log(2/10)- 7/10log(7/10) =0.8018。
这个时候,我们可以说第二个数据集比第一个数据集更确定。容易解释,在第二个数据集中,大部分的数据都能够确定在7/10所对应的数据中,因此可以说更加的确定,混乱度越低。更极端的,如果一个数据集对应的比重为{1,0,0},那么H=0,数据的混乱度为0,能够直接确定数据在第一个类别中。
决策树的划分依据:选取某个特征,样本经过该特征进行分类后,得到的几个子集有最低的信息熵,它相对于原来的数据集就有最大的信息增益(信息增益=原来样本信息熵-划分后样本的信息熵)。接着在得到的子集上再通过信息熵来进一步选择某特征,使得继续划分得到的子集有最低的信息熵。以此类推,直到树的深度满足要求,或者当前树的的节点数据已经能够完全确定了。
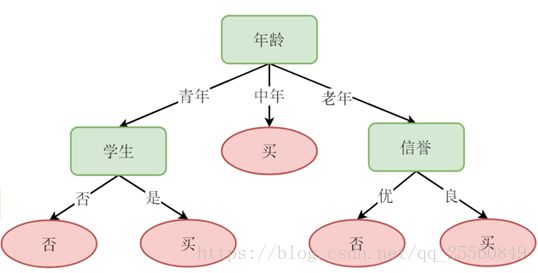
举例如图所示,对于判断一个人是否会购买物品的的决策树,原始数据集有年龄、信誉和是否为学生这3个特征,假设原始的数据集对应的信息熵为H0。现在用年龄划分为{青年,中年,老年}与用其他2个特征划分得到的结果相比,拥有最低的信息熵,即信息增益最大,那么第一个划分的依据就选择年龄。接下来,划分得到的子数据集继续考察除了年龄外的其他特征,对于青年,发现用是否为学生这个特征能够得到最低的信息熵,因此采用是否为学生这个特征;对于中年,发现样本都确定为某一类,所以就不用继续划分;对于老年,发现用信誉这个特征能够得到最低的信息熵,因此采用信誉这个特征。这样就得到了最终的决策树。
3.ID3算法代码实现
为了模拟,我们先创建一个数据集,该数据集有2个特征,分别代表是否可以浮出水面、是否有脚蹼。用1代表是,0代表否。最后一列数据表示当前样本是否为鱼类。【该代码和例子取自机器学习实战】
def createDataSet():
dataSet = [[1, 1, 'yes'], #例如这个样本点代表不能浮出水面、有脚蹼,是鱼类
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing','flippers'] #label记录样本的特征名称
return dataSet, labels输入数据集,计算该数据集所对应的信息熵的值。
from math import log
def calcShannonEnt(dataSet): #输入数据集,计算信息熵
numEntries = len(dataSet) #计算有多少个样本
labelCounts = {} #创建一个字典,用于保存样本的标签,以及该标签对应的数量
for featVec in dataSet: #遍历所有样本
currentLabel = featVec[-1] #将每个样本的最后一列,即标签取出
if currentLabel not in labelCounts.keys(): #如果该标签不在字典中,就加入该标签,并且将数目置为0
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 #将该标签对应的数量加1
shannonEnt = 0.0 #初始化香农熵为0
for key in labelCounts: #遍历字典,计算出最初的香农熵的值
prob = float(labelCounts[key])/numEntries #计算每类标签所占的比重
shannonEnt -= prob * log(prob,2) #计算出香农熵,log的底为2
return shannonEnt下面的代码实现的逻辑是给定特征,并选取该特征下对应的某个值,依据该值将数据划分为子数据集,并将该特征维度给去除掉,用于进一步划分。
def splitDataSet(dataSet, axis, value):#给定数据集、划分数据集的特征、特征所对应的值
retDataSet = [] #创建一个备份数据集,避免原始数据被修改
for featVec in dataSet: #遍历数据集
if featVec[axis] == value: #该特征维度下和value值相等的样本划分到一起,并将该特征去除掉维度去掉
reducedFeatVec = featVec[:axis] #将axis维度两边的数据进行拼接,就将该特征维度给去除掉
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet有了上面的基础代码,现在进行决策树的生成。
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #numfeature为特征的维度,因为最后一列为标签,所以需要减去1
baseEntropy = calcShannonEnt(dataSet) #用来记录最小信息熵,初始值为原始数据集对应的信息熵
bestInfoGain = 0.0; bestFeature = -1 #信息增益初始化为0,最优的划分特征初始化为-1
for i in range(numFeatures): #遍历所有的特征
featList = [example[i] for example in dataSet] #创建list用来存每个样本在第i维度的特征值
uniqueVals = set(featList) #获取该特征下的所有不同的值,即根据该特征可以划分为几类
newEntropy = 0.0 #初始化熵为0
for value in uniqueVals: #遍历该特征维度下对应的所有特征值
subDataSet = splitDataSet(dataSet, i, value) #依据这个值,将样本划分为几个子集,有几个value,就有几个子集
prob = len(subDataSet)/float(len(dataSet)) #计算p值
newEntropy += prob * calcShannonEnt(subDataSet) #计算每个子集对应的信息熵,并全部相加,得到划分后数据的信息熵
infoGain = baseEntropy - newEntropy #将原数据的信息熵-划分后数据的信息熵,得到信息增益
if (infoGain > bestInfoGain): #如果这个信息增益比当前记录的最佳信息增益还大,就将该增益和划分依据的特征记录下来
bestInfoGain = infoGain
bestFeature = i
return bestFeature #returns an integer这里我们只是对于原始数据集选择出了一个特征进行划分,实际上如果划分后的样本还有多个类别,那么还必须进一步划分,因此需要递归创建出决策树。在给出最终创建决策树的代码前,首先解决一个问题,假设特征都用完标签还不唯一,这时又无法继续选择某特征进行划分,那么怎么办?解决的方法就是投票,在这个数据集中,哪个的标签最多,就设这个数据集就就代表着这一类别,这有些类似KNN的思想。
def majorityCnt(classList):
classCount={}
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1 #计算每个标签对应的数目
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)#从大到小进行排列
return sortedClassCount[0][0]#选出标签数量最多的返回接下来就结合上面的全部模块,得出决策树的最终代码。
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet] #存储所有样本的标签
if classList.count(classList[0]) == len(classList):
return classList[0] #如果所有的标签都是一样,就直接返回该子集的标签,这里用的方法是计算其中某个类别的标签数量,如果该数量就等于标签的总数,那容易知道,该数据集的类别标签是一样的
if len(dataSet[0]) == 1: #如果样本的特征值就剩一个,即样本长度为1,就停止,返回该数据集标签数目最多,作为该数据集的标签
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) #选取出该数据集最佳的划分特征
bestFeatLabel = labels[bestFeat] #得出该特征所对应的标签名称
myTree = {bestFeatLabel:{}} #创建mytree字典,这个字典将会一层套一层,这个看后面的结果就明白
del(labels[bestFeat]) #将这个最佳的划分特征从标签名称列表中删除,这是为了下次递归进来不会发生错误的引用,因为下面每次递归的数据集都会删除划分特征所对应的那一列
featValues = [example[bestFeat] for example in dataSet] #获取到该划分特征下对应的所有特征值
uniqueVals = set(featValues) #经过set去重,值代表着该特征能将当前的数据集划分成多少个不同的子集
for value in uniqueVals: #现在对划分的子集进一步进行划分,也就是递归的开始
subLabels = labels[:] #将样本标签复制给sublabels,这样就不会在每次的递归中改变原始labels
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat,value),subLabels)#将样本划分的子集再进行迭代
return myTree运行代码
madat,labels = createDataSet()
mytree = createTree(madat,labels)
mytree![]()
得出来的结果并不是很直观,现将该结果进行图像绘制。以下的代码不做解释,当做模块使用即可。
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def getNumLeafs(myTree):
numLeafs = 0
#firstStr = myTree.keys()[0]
firstSides = list(myTree.keys())
firstStr = firstSides[0]#找到输入的第一个元素
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs +=1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 1
firstSides = list(myTree.keys())
firstStr = firstSides[0]#找到输入的第一个元素
#firstStr = myTree.keys()[0] #注意这里和机器学习实战中代码不同,这里使用的是Python3,而在Python2中可以写成这种形式
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]) == dict:
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
firstSides = list(myTree.keys())
firstStr = firstSides[0]#找到输入的第一个元素
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
plotTree(secondDict[key],cntrPt,str(key))
else:
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
#createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
plotTree(inTree, (0.5,1.0), '')
plt.show()
mytree= retrieveTree(0)
createPlot(mytree)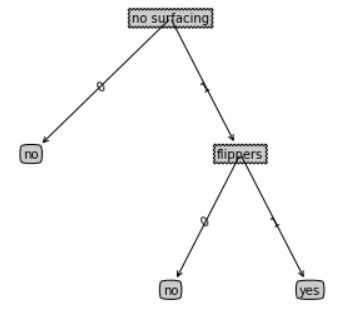
现在使用得到的决策树进行样本分类。
def classify(inputTree,featLabels,testVec):
firstSides = list(myTree.keys())
firstStr = firstSides[0]#找到输入的第一个元素
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
key = testVec[featIndex]
valueOfFeat = secondDict[key]
if isinstance(valueOfFeat, dict): #进行递归
classLabel = classify(valueOfFeat, featLabels, testVec)
else: classLabel = valueOfFeat
return classLabellabels = ['no surfacing','flippers']
classify(mytree,labels,[1,0])![]()
ID3算法比较简单直接,但是存在着很多问题,首先是不能进行数值型数据的处理,即使将数值型数据转化成标称型数据,还会面临特征值过多的问题。
4.基尼系数
其实除了信息熵,还可以通过基尼系数度量数据集的无序程度。公式如下。其划分的效果和用信息熵公式效果差不多,但是基尼系数的计算速度比信息熵稍快。
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(max_depth=2,criterion="gini") #改变判断条件
dt.fit(x,y)二、CART
1.概念
cart是classification and regress tree的缩写,就是该决策树可以同时用于分类和回归问题。这也是sklearn中使用的方式,构建出来的树为二叉树。它的预测复杂度为O(logm),训练复杂度为O(n*m*logm),其中m为样本数,n为特征数。对于多样本和多特征的数据,这样的复杂度是比较高的,此外决策树还可能会过拟合。为此,必须进行“剪枝”:降低复杂度和解决过拟合。
2.cart和决策树的超参数
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
x,y = datasets.make_moons(noise=0.25,random_state =666)
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==0,1],x[y==1,1])
plt.show()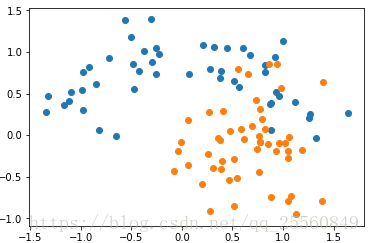
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier()
dt.fit(x,y) #可以看到默认的参数设置
plot_decision_boundary(dt,axis=[-1.5,2.5,-1.0,3])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()决策边界非常不规则,明显产生了过拟合的现象,现在输入参数进行调整。
dt = DecisionTreeClassifier(max_depth=2) #调整决策树深度为2。dt = DecisionTreeClassifier(min_samples_split=10) #设置最小划分的样本数,如果低于这个数,将不再进一步划分dt = DecisionTreeClassifier(max_leaf_nodes=4) #最多就4个叶子节点3.决策树解决回归问题
当用决策树解决分类问题时,最终返回的是叶子节点对应的类别,在用于解决回归问题时,返回的是该节点下样本y值的平均值。当然这里采用的是CART。下面采用sklearn封装的决策树解决回归问题。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
x = boston.data
y = boston.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state =666)
from sklearn.tree import DecisionTreeRegressor
dt = DecisionTreeRegressor()
dt.fit(x_train,y_train)dt.score(x_test,y_test) #0.6962532439825656
dt.score(x_train,y_train) #1 数据在训练数据中完成分类正确,明显出现了过拟合,需要进行调参4.决策树局限性
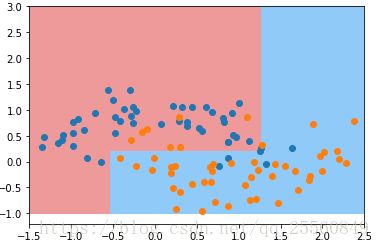
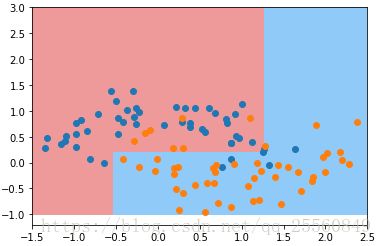
决策边界是横平竖直的,对于倾斜的数据不能够很好地区分。例如下图,对于倾斜的数据,如果x取比较小的数据时,就会根据左边最底下的那根线进行划分,而x取非常大的数据时,就会根据右边最上面的那根线进行划分,数据划分可能会错的离谱。解决办法是PCA降维。
另外对决策树对单点比较敏感,可能会直接导致生成不同的决策边界。解决办法是随机森林。