决策树
决策树
决策树是一种基本的分类方法,当然也可以用于回归。决策树模型呈树形结构。在分类问题中,表示基于特征对实例进行分类的过程,它可以认为是if-then规则的集合。在决策树的结构中,每一个实例都被一条路径或者一条规则所覆盖。通常决策树学习包括三个步骤:特征选择、决策树的生成和决策树的修剪
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理逻辑回归等不能解决的非线性特征数据
缺点:可能产生过度匹配问题
适用数据类型:数值型和标称型
特征选择
特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率,如果利用一个特征进行分类的结果与随机分类的结果没有很大差别,则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的京都影响不大。通常特征选择的准则是信息增益,这是个数学概念。通过一个例子来了解特征选择的过程。
| ID | 年龄 | 有工作 | 有自己的房子 | 信贷情况 | 类别 |
|---|---|---|---|---|---|
| 1 | 青年 | 否 | 否 | 一般 | 否 |
| 2 | 青年 | 否 | 否 | 好 | 否 |
| 3 | 青年 | 是 | 否 | 好 | 是 |
| 4 | 青年 | 是 | 是 | 一般 | 是 |
| 5 | 青年 | 否 | 否 | 一般 | 否 |
| 6 | 中年 | 否 | 否 | 一般 | 否 |
| 7 | 中年 | 否 | 否 | 好 | 否 |
| 8 | 中年 | 是 | 是 | 好 | 是 |
| 9 | 中年 | 否 | 是 | 非常好 | 是 |
| 10 | 中年 | 否 | 是 | 非常好 | 是 |
| 11 | 老年 | 否 | 是 | 非常好 | 是 |
| 12 | 老年 | 否 | 是 | 好 | 是 |
| 13 | 老年 | 是 | 否 | 好 | 是 |
| 14 | 老年 | 是 | 否 | 非常好 | 是 |
| 15 | 老年 | 否 | 否 | 一般 | 否 |
我们希望通过所给的训练数据学习一个贷款申请的决策树,用以对文莱的贷款申请进行分类,即当新的客户提出贷款申请是,根据申请人的特征利用决策树决定是否批准贷款申请。特征选择其实是决定用那个特征来划分特征空间。下图中分别是按照年龄,还有是否有工作来划分得到不同的子节点。
问题是究竟选择哪个特征更好些呢?那么直观上,如果一个特征具有更好的分类能力,是的各个自己在当前的条件下有最好的分类,那么就更应该选择这个特征。信息增益就能很好的表示这一直观的准则。这样得到的一棵决策树只用了两个特征就进行了判断:
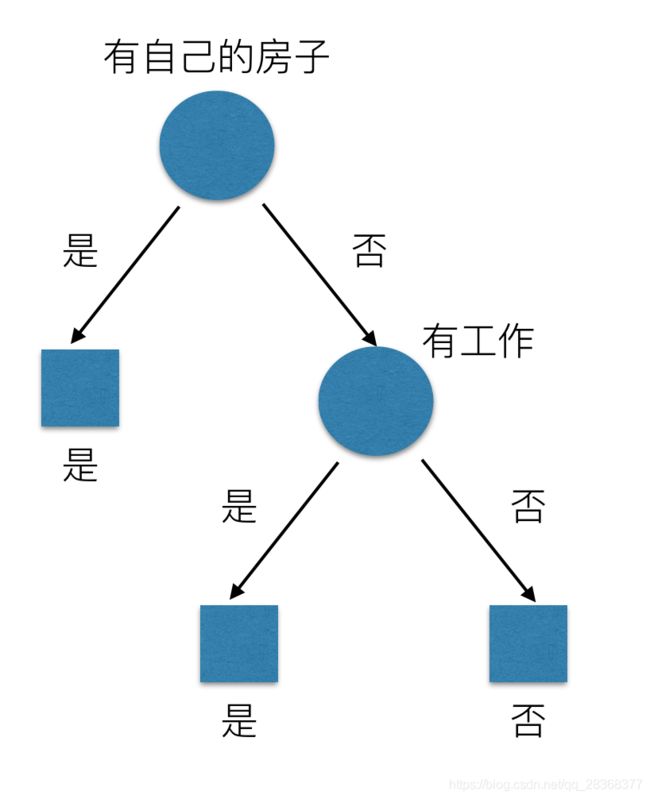
通过信息增益生成的决策树结构,更加明显、快速的划分类别。下面介绍scikit-learn中API的使用
信息的度量和作用
我们常说信息有用,那么它的作用如何客观、定量地体现出来呢?信息用途的背后是否有理论基础呢?这个问题一直没有很好的回答,直到1948年,香农在他的论文“通信的数学原理”中提到了“信息熵”的概念,才解决了信息的度量问题,并量化出信息的作用。
一条信息的信息量与其不确定性有着直接的关系,比如我们要搞清一件非常不确定的事,就需要大量的信息。相反如果对某件事了解较多,则不需要太多的信息就能把它搞清楚 。所以从这个角度看,可以认为,信息量就等于不确定的多少。那么如何量化信息量的度量呢?2022年举行世界杯,大家很关系谁是冠军。假如我错过了看比赛,赛后我问朋友 ,“谁是冠军”?他不愿意直接告诉我,让我每猜一次给他一块钱,他告诉我是否猜对了,那么我需要掏多少钱才能知道谁是冠军?我可以把球编上号,从1到32,然后提问:冠 军在1-16号吗?依次询问,只需要五次,就可以知道结果。所以谁是世界杯冠军这条消息只值五块钱。当然香农不是用钱,而是用“比特”这个概念来度量信息量。一个比特是 一位二进制数,在计算机中一个字节是8比特。
那么如果说有一天有64支球队进行决赛阶段的比赛,那么“谁是世界杯冠军”的信息量就是6比特,因为要多猜一次,有的同学就会发现,信息量的比特数和所有可能情况的对数函数log有关,(log32=5,log64=6)
另外一方面你也会发现实际上我们不需要猜五次就能才出冠军,因为像西班牙、巴西、德国、意大利这样的球队夺得冠军的可能性比南非、尼日利亚等球队大得多,因此第一次猜测时不需要把32支球队等分成两个组,而可以把少数几支最有可能的球队分成一组,把其他球队分成一组。然后才冠军球队是否在那几支热门队中。这样,也许三次就猜出结果。因此,当每支球队夺冠的可能性不等时,“谁是世界杯冠军”的信息量比5比特少。香农指出,它的准确信息量应该是:
H = -(p1logp1 + p2logp2 + … + p32log32)
其中,p1…p32为这三支球队夺冠的概率。H的专业术语称之为信息熵,单位为比特,当这32支球队夺冠的几率相同时,对应的信息熵等于5比特,这个可以通过计算得出。有一个特性就是,5比特是公式的最大值。那么信息熵(经验熵)的具体定义可以为如下:
H ( X ) = ∑ x ∈ X P ( x ) log P ( x ) H(X)=\sum x \in X P(x) \log P(x) H(X)=∑x∈XP(x)logP(x)
信息增益
自古以来,信息和消除不确定性是相联系的。所以决策树的过程其实是在寻找某一个特征对整个分类结果的不确定减少的过程。那么这样就有一个概念叫做信息增益(information gain)。
那么信息增益表示得知特征X的信息而是的类Y的信息的不确定性减少的程度,所以我们对于选择特征进行分类的时候,当然选择信息增益较大的特征,这样具有较强的分类能力。特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即公式为:
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D, A)=H(D)-H(D | A) g(D,A)=H(D)−H(D∣A)
根据信息增益的准则的特征选择方法是:对于训练数据集D,计算其每个特征的信息增益,并比较它们的阿笑,选择信息增益最大的特征
信息增益的计算
假设训练数据集为D,|D|表示样本个数。设有K个类C_k,k=1,2,3,4…k,|C_k|为属于类C_k的样本个数,
∑ k = 1 K = ∣ D ∣ \sum_{k=1}^{K}{=}{|D|} k=1∑K=∣D∣
.设特征A有n个不同的取值{a1,a2,…,an},根据特征A的取值将D划分为n个子集D1,D2,…,Dn,|Di|为样本个数,其中Di中属于Ck类的样本的集合为D_ik
所以首先对于经验熵来说,计算如下:
H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log \frac{\left|C_{k}\right|}{|D|} H(D)=−k=1∑K∣D∣∣Ck∣log∣D∣∣Ck∣
那么条件熵计算如下:
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 K ∣ D i k ∣ ∣ D i ∣ log ∣ D i k ∣ ∣ D i ∣ H(D | A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \sum_{k=1}^{K} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} H(D∣A)=i=1∑n∣D∣∣Di∣H(Di)=−i=1∑n∣D∣∣Di∣k=1∑K∣Di∣∣Dik∣log∣Di∣∣Dik∣
既然我们有了这两个公式,我们可以根据前面的是否通过贷款申请的例子来通过计算得出我们的决策特征顺序。那么我们首先计算总的经验熵为:
H ( D ) = − ( 9 / 15 ) log ( 9 / 15 ) − ( 6 / 15 ) log ( 6 / 15 ) = 0.971 H(D)=-(9 / 15) \log (9 / 15)-(6 / 15) \log (6 / 15)=0.971 H(D)=−(9/15)log(9/15)−(6/15)log(6/15)=0.971
然后我们让A1,A2,A3,A4分别表示年龄、有工作、有自己的房子和信贷情况4个特征,则计算出年龄的信息增益为:
g ( D , A 1 ) = H ( D ) − [ ( 5 / 15 ) H ( D 1 ) + ( 5 / 15 ) H ( D 2 ) + ( 5 / 15 ) H ( D 3 ) ] H ( D 1 ) = − ( 2 / 5 ) log ( 2 / 5 ) − ( 3 / 5 ) log ( 3 / 5 ) H ( D 2 ) = − ( 3 / 5 ) log ( 3 / 5 ) − ( 2 / 5 ) log ( 2 / 5 ) H ( D 3 ) = − ( 4 / 5 ) log ( 4 / 5 ) − ( 1 / 5 ) log ( 1 / 5 ) \begin{array}{c}{g(D, A 1)=H(D)-[(5 / 15) H(D 1)+(5 / 15) H(D 2)+(5 / 15) H(D 3)]} \\ {H(D 1)=-(2 / 5) \log (2 / 5)-(3 / 5) \log (3 / 5)} \\ {H(D 2)=-(3 / 5) \log (3 / 5)-(2 / 5) \log (2 / 5)} \\ {H(D 3)=-(4 / 5) \log (4 / 5)-(1 / 5) \log (1 / 5)}\end{array} g(D,A1)=H(D)−[(5/15)H(D1)+(5/15)H(D2)+(5/15)H(D3)]H(D1)=−(2/5)log(2/5)−(3/5)log(3/5)H(D2)=−(3/5)log(3/5)−(2/5)log(2/5)H(D3)=−(4/5)log(4/5)−(1/5)log(1/5)
同理其他的也可以计算出来,g(D,A2)=0.324,g(D,A3)=0.420,g(D,A4)=0.363,相比较来说其中特征A3(有自己的房子)的信息增益最大,所以我们选择特征A3为最有特征。
DecisionTreeRegressor
-
DecisionTreeRegressor是回归决策树,其原型为:class sklearn.tree.DecisionTreeRegressor(criterion='mse', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None,random_state=None, max_leaf_nodes=None, presort=False)-
criterion:一个字符串,指定切分质量的评价准则。默认为
'mse',且只支持该字符串,表示均方误差。 -
splitter:一个字符串,指定切分原则。可以为:'best':表示选择最优的切分。'random':表示随机切分。
-
max_features:可以为整数、浮点、字符串或者None,指定寻找最优拆分时考虑的特征数量。- 如果是整数,则每次切分只考虑
max_features个特征。 - 如果是浮点数,则每次切分只考虑
max_features * n_features个特征,max_features指定了百分比。 - 如果是字符串
'sqrt',则max_features等于sqrt(n_features)。 - 如果是字符串
'log2',则max_features等于log2(n_features)。 - 如果是
None或者'auto',则max_features等于n_features。
注意:如果已经考虑了
max_features个特征,但是还没有找到一个有效的切分,那么还会继续寻找下一个特征,直到找到一个有效的切分为止。 - 如果是整数,则每次切分只考虑
-
max_depth:可以为整数或者None,指定树的最大深度。-
如果为
None,则表示树的深度不限。分裂子结点,直到每个叶子都是纯的(即:叶结点中所有样本点都属于一个类),或者叶结点中包含小于
min_samples_split个样点。 -
如果
max_leaf_nodes参数非None,则忽略此选项。
-
-
min_samples_split:为整数,指定每个内部结点包含的最少的样本数。 -
min_samples_leaf:为整数,指定每个叶结点包含的最少的样本数。 -
min_weight_fraction_leaf:为浮点数,叶结点中样本的最小权重系数。 -
max_leaf_nodes:为整数或者None,指定最大的叶结点数量。- 如果为
None,此时叶结点数量不限。 - 如果非
None,则max_depth被忽略。
- 如果为
-
class_weight:为一个字典、字符串'balanced'、或者None。它指定了分类的权重。- 如果为字典,则权重的形式为:
{class_label:weight}。 - 如果为字符串
'balanced',则表示分类的权重是样本中各分类出现的频率的反比。 - 如果为
None,则每个分类的权重都为1 。
注意:如果提供了
sample_weight参数(由fit方法提供),则这些权重都会乘以sample_weight。 - 如果为字典,则权重的形式为:
-
random_state:指定随机数种子。 -
presort:一个布尔值,指定是否要提前排序数据从而加速寻找最优切分的过程。- 对于大数据集,设置为
True会减慢总体的训练过程。 - 对于一个小数据集或者设定了最大深度的情况下,设置为
True会加速训练过程。
- 对于大数据集,设置为
-
-
模型属性:
feature_importances_:给出了特征的重要程度。该值越高,则该特征越重要。max_features_:max_features的推断值。n_features_:当执行fit之后,特征的数量。n_outputs_:当执行fit之后,输出的数量。tree_:一个Tree对象,即底层的决策树。
-
模型方法:
fit(X, y[, sample_weight, check_input, ...]):训练模型。predict(X[, check_input]):用模型进行预测,返回预测值。score(X,y[,sample_weight]):返回模型的预测性能得分。
注意:所有基于树的回归模型不能外推,也不能在训练数据范围之外进行预测。
计算机内存(RAM)历史价格预测
import pandas as pd
import matplotlib.pyplot as plt
ram_prices = pd.read_csv('ram_price.csv')
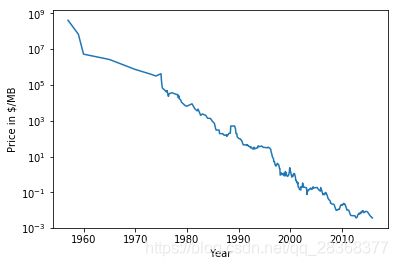
plt.semilogy(ram_prices.date,ram_prices.price) # 用对数坐标绘制RAM价格的发展历史
plt.xlabel('Year')
plt.ylabel('Price in $/MB')
plt.show()
数据图像,x轴为日期,y轴为那一年1MB的计算机内存的价格:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
ram_prices = pd.read_csv('ram_price.csv')
data_train = ram_prices[ram_prices.date<2000]
data_test = ram_prices[ram_prices.date>=2000]
# 基于日期预测价格
X_train = data_train.date[:,np.newaxis] #np.newaxis是增加维度,如1维变2维
y_train = np.log(data_train.price) #这里np.log()是以e为底的对数
tree = DecisionTreeRegressor().fit(X_train,y_train)
#对所有数据进行预测
X_all = ram_prices.date[:,np.newaxis]
pred_tree = tree.predict(X_all)
#进行对数变换逆运算
price_tree = np.exp(pred_tree)
#决策树预测结果与真实值对比
plt.figure(figsize=(10,8),dpi=80)
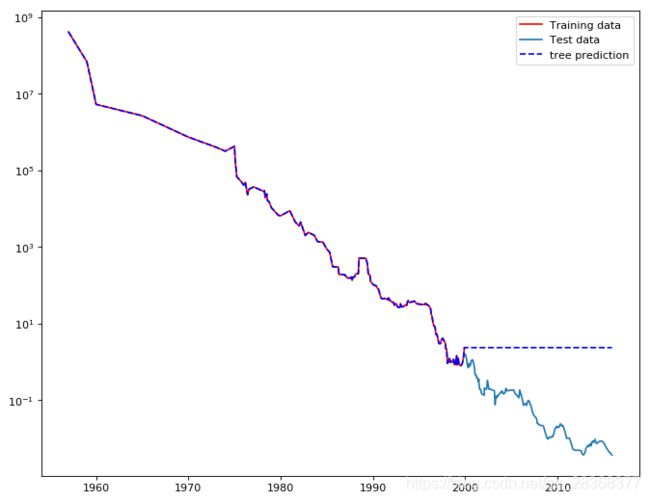
plt.semilogy(data_train.date,data_train.price,'r',label='Training data')
plt.semilogy(data_test.date,data_test.price,label='Test data')
plt.semilogy(ram_prices.date,price_tree,'--b',label='tree prediction')
plt.legend()
plt.show()
树模型完美的预测了训练数据,但是一旦超出训练集数据范围,模型就只能持续预测最后一个已知数据点。树不能在训练数据范围外生成“新的”响应。所有基于树的模型都有这个缺点。
DecisionTreeClassifier
-
DecisionTreeClassifier是分类决策树,其原型为:sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None,min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None,random_state=None, max_leaf_nodes=None, class_weight=None,presort=False)criterion:一个字符串,指定切分质量的评价准则。可以为:'gini':表示切分时评价准则是Gini系数'entropy':表示切分时评价准则是熵
- 其它参数参考
DecisionTreeRegressor。
-
模型属性:
classes_:分类的标签值。n_classes_:给出了分类的数量。- 其它属性参考
DecisionTreeRegressor。
-
模型方法:
fit(X, y[, sample_weight, check_input, ...]):训练模型。predict(X[, check_input]):用模型进行预测,返回预测值。predict_log_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率的对数值。predict_proba(X):返回一个数组,数组的元素依次是X预测为各个类别的概率值。score(X,y[,sample_weight]):返回模型的预测性能得分。
决策图
当训练完毕一棵决策树的时候,可以通过sklearn.tree.export_graphviz(classifier,out_file)来将决策树转化成Graphviz格式的文件。
安装Graphviz和pydot模块将dot文件转换为图片png。
这里我在 win10系统下利用的 conda 进行安装,命令conda install graphviz,安装完成后配置 graphviz 的环境变量D:\Anaconda3\Library\bin\graphviz,然后重启电脑。再安装pydot模块。
注意:必须安装graphviz,不然会报错。
乳腺癌分类
(用于二分类,良性和恶性)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import export_graphviz
import pydot
cancer = load_breast_cancer()
X_train,X_test,y_train,y_test = train_test_split(cancer.data,cancer.target,
test_size=0.25,random_state=0)
tree = DecisionTreeClassifier(max_depth=5,random_state=1)
tree.fit(X_train,y_train)
print('训练集精度:{:.3f}'.format(tree.score(X_train,y_train)))
print('测试集精度:{:.3f}'.format(tree.score(X_test,y_test)))
#决策树特征的重要程度
print('树的特征的重要程度:\n{}'.format(dtc.feature_importances_))
n_features = cancer.data.shape[1]
#print(n_features)
plt.figure(figsize=(10,8),dpi=80)
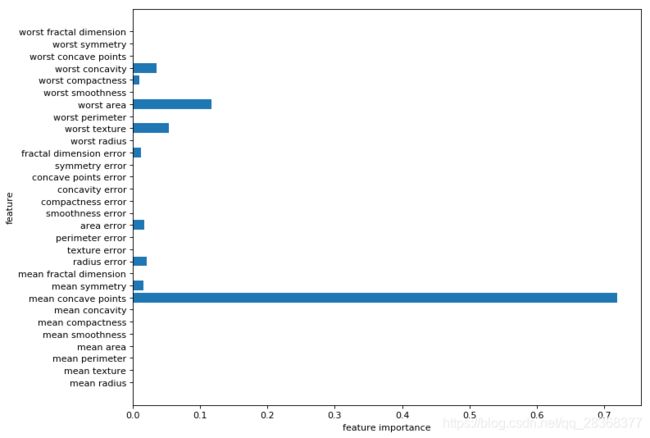
plt.barh(range(n_features),dtc.feature_importances_,align='center')
plt.yticks(np.arange(n_features),cancer.feature_names)
plt.xlabel('feature importance')
plt.ylabel('feature')
plt.show()
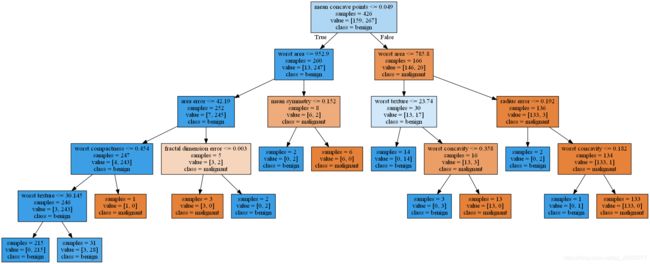
#生成dot文件
export_graphviz(dtc,out_file='tree.dot',class_names=cancer.target_names,
feature_names=cancer.feature_names,impurity=False,filled=True)
#利用pydot将dot文件转换为图片png
(graph,) = pydot.graph_from_dot_file('tree.dot')
graph.write_png('决策图.png')
训练集精度:0.993
测试集精度:0.937
树的特征的重要程度:
[0. 0. 0. 0. 0. 0.
0. 0.71911276 0.01547265 0. 0.02002456 0.
0. 0.01722965 0. 0. 0. 0.
0. 0.01237812 0. 0.05346217 0. 0.1169146
0. 0.0100243 0.03538118 0. 0. 0. ]
决策树的优缺点:
| 优点 | 缺点 |
|---|---|
| 模型容易可视化(较小的树) | 经常会过拟合,泛化能力差 |
| 完全受数据缩放的影响(不需要归一化、标准化) |
对于决策树的缺点解决方法:
- 预减枝策略(设置max_depth、max_leaf_nodes、min_samples_leaf)
- 采用集成方法:随机森林和梯度提升决策
参考资料
《黑马程序员之机器学习》《python机器学习基本教程》《python机器学习应用》《AI算法工程师手册》