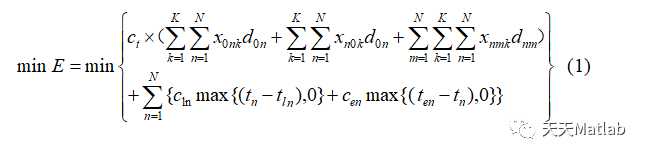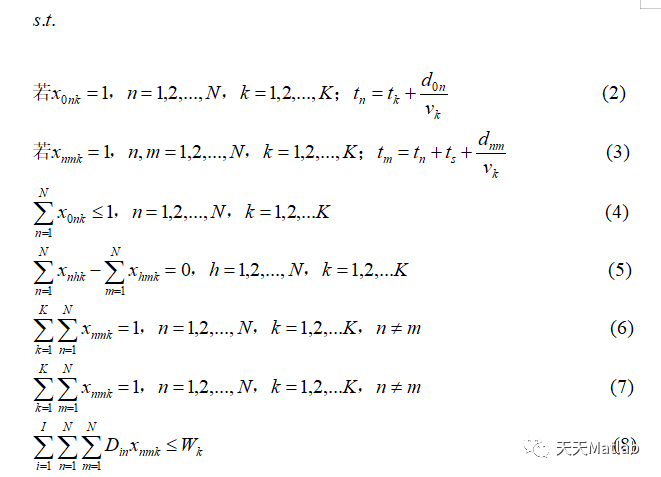【优化求解】模拟退火遗传实现带时间窗的车辆路径规划问题

带时间窗的VRP问题描述：

假设在一个供求关系系统中，车辆从货源取货，配送到对应的若干配送点。车辆存在最大载货量，且配送可能有时间限制。需要合理安排取货时间，组织适当的行车路线，使用户需求得到满足，同时使某个代价函数最小，比如总工作时间最少、路径最短等。可以看出TSP问题是VRP问题的一种简单特殊形式。因此，VRP也是一种NP hard 问题。

目前解决此种问题的办法有多种，主要以启发式算法为主。包括退火算法、遗传算法、蚁群算法、禁忌算法等。

下面建立带时间窗的VRP模型：

 

 

 

 

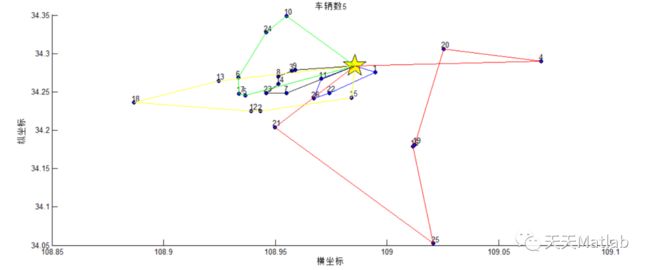
clc;clear allclose allt0=cputime;%计时开始filename='.\Solomon\c101.txt';[NO,XCOORD, YCOORD,DEMAND,READY_TIME,DUE_DATE,SERVICE_TIME]=textread(filename,'%s%s%s%s%s%s%s','headerlines',8);%初始化timewindows=[str2num(char(READY_TIME))';str2num(char(DUE_DATE))'];coordinate=[str2num(char(XCOORD)),str2num(char(YCOORD))];demand=str2num(char(DEMAND))';service=str2num(char(SERVICE_TIME))';D=distanse(coordinate);popsize=80;%种群数量capacity = 200;%车子载重%经验公式m=[Σgi /aq]＋1,粗求车辆数a = 0.8;   %【3】k1 = round((sum(abs(demand))./(a*capacity)))-2;    %最小车辆数k2 = round((sum(abs(demand))./(a*capacity)))+1;    %最大车辆数% k1=size(NO);% k2=k1+10;original = 100;%初始每辆车的载货量C=500;%C为停止代数，遗传到第 C代时程序停止,C的具体取值视问题的规模和耗费的时间而定Pc=0.9;%交叉概率Pm=0.4;%变异概率%  R = zeros(1,n+k);% tempR = zeros(1,n+k);minvalue = 1000000;%随便设置的最优值，不能太小for k = k1:1:k2 %每种车辆数做一次寻优         [tempR,tempvalue] = Run_VRP(D,demand,popsize,timewindows,k,capacity,original,C,Pc,Pm,service);%运算返回最优路径R和其总距离Rlength    if min(tempvalue) < minvalue        minvalue = min(tempvalue);%如果小于最小适应度值，替代&& min(tempvalue)>100               R = tempR;%保存最小路径        minvehicle = k;%保存最小车辆数量            shiyingdu=tempvalue ;%保存最小染色体    end   enddisp(['最优染色体',num2str(R)]);disp(['最小车辆数',num2str(minvehicle)]);disp(['最小里程数',num2str(minvalue)]); figure(1)sz=100;% scatter(coordinate(:,1),coordinate(:,2),50);%客户位置hold on[n,nn] = size(D);%节点个数for i=2:n    plot(coordinate(i,1),coordinate(i,2),'ro','MarkerSize',5,'MarkerEdgeColor','k','MarkerFaceColor','b');   text(coordinate(i,1)-0.001,coordinate(i,2)+0.005,[num2str(i-1)],'Fontsize',10);hold onendhold onplot(coordinate(1,1),coordinate(1,2),'p','MarkerSize',30,'MarkerEdgeColor','k','MarkerFaceColor','y');hold on%发货中心ss=0;cost=zeros(k,1);for j=1:length(R)-1    if R(j)==0        ss=ss+1;    end    switch ss        case 1            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)]);hold on%%画出车辆1的路程                 case 2            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','r');hold on%%画出车辆2的路程                case 3            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','g');hold on %%画出车辆3的路程                  case 4            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','k');hold on %%画出车辆3的路程                     line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','y');hold on %%画出车辆3的路程                   case 6            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','m');hold on %%画出车辆3的路程                case 7            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[1 0.6 0.3]);hold on %%画出车辆3的路程                 case 8            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.5 0.5 0.5]);hold on %%画出车辆3的路程                   case 9            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.6 0.4 0.7]);hold on %%画出车辆3的路程                  case 10             line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.8 0.4 0.7]);hold on %%画出车辆3的路程               case 11             line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.6 0.6 0.7]);hold on %%画出车辆3的路程                   case 12             line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color',[0.6 0.4 0.7]);hold on %%画出车辆3的路程               otherwise            line([coordinate(R(j)+1,1),coordinate(R(j+1)+1,1)],[coordinate(R(j)+1,2),coordinate(R(j+1)+1,2)],'Color','c');hold on %%画出车辆4的路程              endendminvalue1=sum(cost);title(['车辆数',num2str(minvehicle)]);xlabel('横坐标');ylabel('纵坐标')figure(2)plot(1:C-1,shiyingdu,'b-');xlabel('迭代次数');ylabel('适应度');

•  
•  
•  

最优染色体0   1  22  26  11   0  21  25  16  19  20   4   0   5  17   6  24  10   0   9   3   8  14  23   7   0  13  18  12   2  15   0最小车辆数5最小里程数377.3607

往期回顾>>>>>>

基于栅格地图——遗传算法的机器人最优路径规划

【模式识别】Matlab指纹识别

【基础教程】matlab绘制疫情地图

matlab自动识别银行卡号

【优化问题】遗传算法求最值

无参考图像质量评价之基于多特征的增强图像质量评价

完整源码加qq1575304183